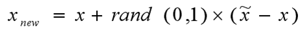摘要
SMOTE是一种综合采样人工合成数据算法,用于解决数据类别不平衡问题(Imbalanced class problem),以Over-sampling少数类和Under-sampling多数类结合的方式来合成数据。本文将以Nitesh V. Chawla(2002)的论文为蓝本,阐述SMOTE的核心思想以及实现其朴素算法,在传统分类器(贝叶斯和决策树)上进行对比算法性能并且讨论其算法改进的途径。
1. 引言
类别不平衡是一种在分类器模型训练过程中常见的问题之一,如通过大量胸透图片来学习判断一个人是否有癌症,又如在网络流日志中学习检测可能是攻击行为的数据模式,这一类的任务中都是正常的类多于异常(诊断属于癌症,属于攻击行为)的类,在类别不平衡数据下训练出来的分类器要非常的小心,即使该分类器拥有很高的精度,因为它很可能会习得大部分的都是正常的,而我们可能需要的是它能够最大程度的识别异常行为,哪怕精度低于前者。
为了解决这一问题,业内已经有以下5种公认的方法去扩充数据集[1],以至于类别均匀:
- 随机的增大少数类的样本数量。
- 随机的增大特定少数类样本的数量。
- 随机的减少多数类样本的数量。
- 随机的减少特定多数类样本的数量。
- 修改代价函数,使得少数类出错的代价更高。
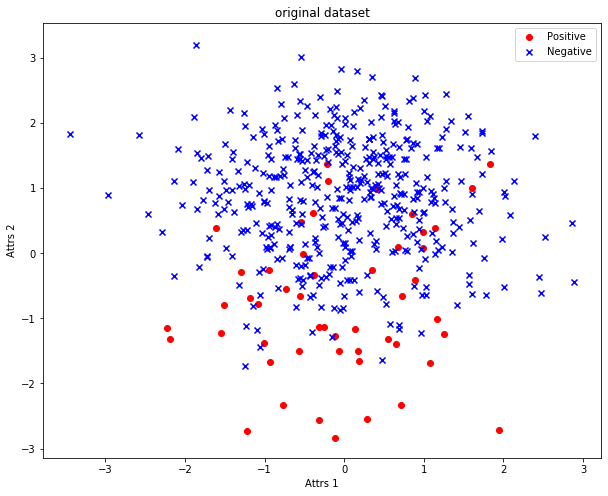
本文要介绍的SMOTE算法就是一种综合1,3方法的改进方式,它以每个样本点的k个最近邻样本点为依据,随机的选择N个邻近点进行差值乘上一个[0,1]范围的阈值,从而达到合成数据的目的。这种算法的核心是:特征空间上邻近的点其特征都是相似的。它并不是在数据空间上进行采样,而是在特征空间中进行采样,所以它的准确率会高于传统的采样方式。这也是为什么到目前为止SMOTE以及其派生的算法仍然是较为主流的采样技术的原因。

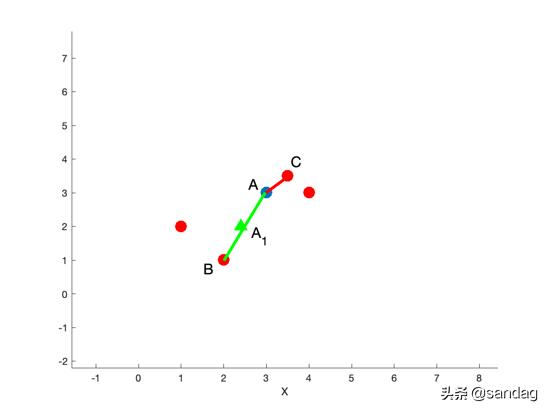
在Figure 1中,假设数据点A在特征空间上有4个邻近点,若N为2,则SMOTE会随机选择其中2个邻近点B,C,分别计算A->B, A->C的距离,如图中绿线和红线所示,在绿线或红线上的所有采样点都是合理的,如点A1。为了确保数据点尽可能的多样(不重叠),故乘上一个[0, 1]之间的随机因子。
本文将会在第2章根据SMOTE的核心以及其伪代码实现该算法,并应用在测试数据集上;第3章会使用第三方imbalanced-learn库中实现的SMOTE算法进行采样,以验证我们实现的算法的准确性,当然这个库中的算法要优于朴素的SMOTE算法,之后我们会以决策树和高斯贝叶斯分类器为工具,对测试原始数据、应用我们所实现的SMOTE采样后产生的数据以及应用第三方库SMOTE产生的数据三者分别产生的数据集进行性能比较;第4章会讨论朴素SMOTE算法更加鲁棒和表现更好的优化途径;第5章是对本文的总结。
2. 算法分析与实现
Fig. 2是在SMOTE论文中提出的伪代码,由两个函数SMOTE(T, N, K)和Populate(N, i, nnarray)组成。

SMOTE负责接受要采样的类数据集X,返回一个经过SMOTE采样后的数据集,大小为(N/100)*T,函数有三个参数,分别是T: 需要处理的数据集X的样本数量; N: 采样比例,一般为100, 200, 300等整百数,对应即1倍,2倍,3倍;K: 为采样的最近邻数量,论文中默认为5。SMOTE代码思想非常简单,扫描每一个样本点,计算每一个样本点的K个最近邻,将每一个最近邻样本点的索引记录在nnarray中,之后传入Populate(N, i, nnarray)中即完成一个样本点的采样。
Populate则负责根据nnarray中的索引去随机生成N个与观测样本i相似的样本。该函数会计算随机邻近点nn与观测样本i点的每一个特征之间的差距dif,将其差距乘上一个[0, 1]随机因子gap,再将dif*gap的值加上观测点i即完成了一个特征的合成。
在Python中实现如下:
注:为了保证本文中所有代码的可复现性,设置的random_state均为666
def NaiveSMOTE(X, N=100, K=5):"""{X}: minority class samples;{N}: Amount of SMOTE; default 100;{K} Number of nearest; default 5;"""# {T}: Number of minority class samples; T = X.shape[0]if N < 100:T = (N/100) * TN = 100N = (int)(N/100)numattrs = X.shape[1]samples = X[:T]neigh = NearestNeighbors(n_neighbors=K)neigh.fit(samples)Synthetic = np.zeros((T*N, numattrs))newindex = 0def Populate(N, i, nns, newindex):"""Function to generate the synthetic samples."""for n in range(N):nn = np.random.randint(0, K)for attr in range(numattrs):dif = samples[nns[nn], attr] - samples[i, attr]gap = np.random.random()Synthetic[newindex, attr] = samples[i, attr] + gap*difnewindex += 1return newindexfor i in range(T):nns = neigh.kneighbors([samples[i]], K, return_distance=False)newindex = Populate(N, i, nns[0], newindex)return Synthetic
这里没有采用矩阵运算,而是完完全全的按照论文中的方式复现(所以称为NaiveSMOTE),其中最近邻的计算我们使用scikit-learn提供的NearestNeighbors类完成。
接下来我们使用scikit-learn中的make_classification来生成测试分类数据集,模拟不平衡类数据,当然有兴趣的读者也可以去寻找论文中所使用的数据集。
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=500,n_features=9,n_redundant=3,weights=(0.1, 0.9),n_clusters_per_class=2,random_state=666) # 为了可复现性
print(X.shape, y.shape) # ((500, 9), (500,))# 查看y的各类样本数
print(view_y(y)) # class 0: 50 class 1: 450
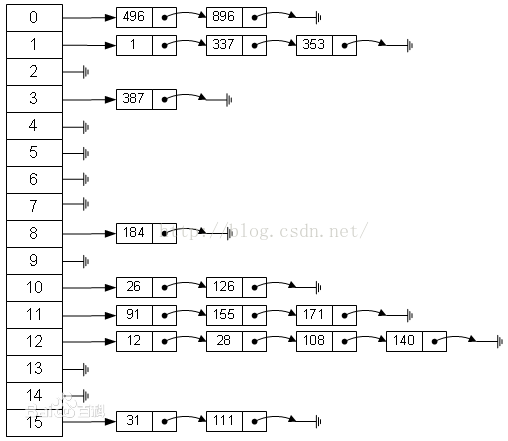
原数据集的分布如Fig. 3所示,其中红色圆圈为正类即少数类,蓝色×为负类即多数类。
将我们实现的NaiveSMOTE应用在此测试数据上:
X_over_sampling = NaiveSMOTE(X[y==0], N=800)
print(X_over_sampling.shape) # (400, 9) 新增了400个样本# 将合成数据与原数据集合并
new_X = np.r_[X, X_over_sampling]
new_y = np.r_[y, np.zeros((X_over_sampling.shape[0]))]
print(new_X.shape, new_y.shape) # ((900, 9), (900,))print(view_y(new_y)) # class 0: 450 class 1: 450
接下来我们将原数据集与经过NaiveSMOTE合成后的数据集进行比对:
可以很清晰的看见原来的类增大至一个满意的水平,并且生成的类之间距离都相距不远。
3. 算法性能比对
本章我们将引入第三方库imbalanced-learn中提供的SMOTE类与依据论文实现的NaiveSMOTE进行比较。两者都是基于同一个论文的思想去实现的,只是第三方库中实现的SMOTE更为鲁棒,并且能够综合考虑所有的类,是一种完全意义上的Combination of Over-sampling minority class and Under-sampling majority class技术。因此我们引入它只为了验证我们所复现的方法的准确性。
from imblearn.over_sampling import SMOTEsm = SMOTE(random_state=666)
X_res, y_res = sm.fit_resample(X, y) # 即完成了合成
print(X_res.shape, y_res.shape) # ((900, 9), (900,))
下图对比imblearn的SMOTE与我们复现的NaiveSMOTE生成的数据集:
能看出NaiveeSMOTE合成的数据更加倾向于中部,而第三方的SMOTE能够综合考虑全局情况下方区域生成的数据要比NaiveSMOTE的多。
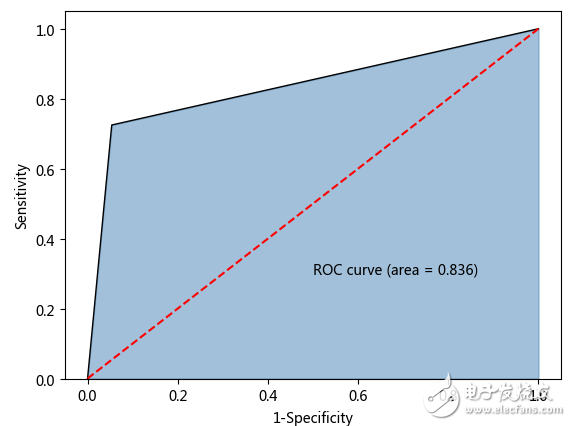
接下来我们使用DecisionTree和GaussianNaive来验证3个数据集(原数据集、NaiveSMOTE合成的数据集和第三方SMOTE合成的数据集)的ROC曲线,具体代码见附录中的Notebook文件
原数据的ROC曲线
NaiveSMOTE生成的数据的ROC曲线
第三方SMOTE生成的数据的ROC曲线
可以看出NaiveSMOTE与imblearn的SMOTE生成的数据的AUC面积均大于原始数据的面积。imblearn的SMOTE生成的数据在GaussianNaiveBayes分类器上的表现要好于NaiveSMOTE所生成的数据训练出来的分类器。
4. 算法改进
这部分我们从NaiveSMOTE的三个方面进行优化讨论:
-
处理速度。
NaiveSMOTE中有许多处都可以改成使用矩阵运算的方式,这样会提高数据处理的速度。并且Populate函数也显得非常冗余,可以用矩阵运算将其改写。 -
全局合理性。
全局合理性包括两个方面:合成数据比率的合理性和合成数据在全局的合理性。合成数据比率的合理性:在
NaiveSMOTE中可以知道样本的数量有N合成比率来控制,只能合成其整数倍,本文中使用的数据集恰好是1:9,只要合成原始数据的8倍即可是两类都到达一个相对数量同等的水平,但是在现实数据集中大部分都不具备成倍的数量关系,因此可以考虑更换一个更好的生成比率,使得每个类均能处于相对数量近似的水平,避免出现合成后的原少数类变多数类的情况。合成数据在全局的合理性:回想在
NaiveSMOTE与imblearn SMOTE各自合成的数据对比中可以发现,NaiveSMOTE更加容易使得合成的数据聚集在某一样本点附近,而imblearn SMOTE所合成的数据更为稀疏且分布均匀,更加接近原始数据的概率分布。其原因在于NaiveSMOTE在进行合成时只考虑原始的数据样本,没不考虑合成后的数据样本会如何影响全局数据。可以考虑在每次合成数据后将其加入数据集,在处理过程中将合成数据也加入考虑范围。 -
鲁棒性。
不难发现NaiveSMOTE仅能够处理数值型的数据并且其距离计算公式很有可能产生误解。在现实中有许多非数值型的数据,如性别,职业等等。当然可以将其全部重新编码成可以应用数值处理的数据,如将性别进行OneHot编码,但是此时的距离计算公式就会出现误解,可以考虑更换为欧氏距离、曼哈顿距离或者马氏距离等。
Note:在对性别进行OneHot编码时情况如下:
男性: 0 1
女性: 1 0
如果按照NaiveSMOTE原始的距离计算公式,很有可能会将其理解为男性和女性的差距为1,因此产生误解。
5. 结论
本文对三种数据进行对比,经过NaiveSMOTE和imblearn SMOTE合成后的数据在传统分类器上的表现均好于原始数据(即不做任何修改),且imblearn SMOTE在鲁棒性上要高于NaiveSMOTE。讨论NaiveSMOTE的不足与其可能的优化方向。建议在实际应用中优先考虑鲁棒性更高的imlearn SMOTE而不是自己造轮子,imblearn SMOTE的实现更加符合主流标准。但不能因此就忽略了NaiveSMOTE的意义,任何的优化有必要要基于原有的基础。理解NaiveSMOTE才能去更好的使用和优化它。
附录
实验Notebook
参考文献
- Japkowicz, Nathalie, and Shaju Stephen. “The class imbalance problem: A systematic study.” Intelligent data analysis 6.5 (2002): 429-449.

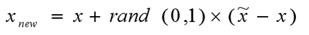




![[12]机器学习_smote算法](https://img-blog.csdnimg.cn/83d6c9cccbce4f6fa9e690046559280f.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5pep5bed5qmZ,size_20,color_FFFFFF,t_70,g_se,x_16)