公式符号

CSDN-MarkDown编辑器使用的公式定界符为$和$$，单美元符号包围的是行内公式，双美元符号包围的是块公式。
行内公式，只在同一行内，单美刀符号：$公式内容在同一行$
块公式，要另一起行且居中，双美刀符号：$$公式内容另起一行且居中$$

超过一个字符时使用{ }括起来
注意，$内部写的中括号{ }不会显示出来。需要加斜杠 \{ \}

1.上下标 ^ _

^表上标，_表下标。若字符多余一个，用{ }括起来

$x^{y^z}=(1+e^x{)}^{-2x{y}^w}$ :$x^{y^z}=(1+e^x)^{-2xy^w}$

2.分子分母 \frac{}{}

$\frac{1}{n}$：$\frac{1}{n}$
放大加d：\dfrac{}{}

3.根号 \sqrt

开n次方：\sqrt[n]{内容}：$\sqrt[n]{内容}$

$\sqrt{b^2 - 4ac}$：$\sqrt{b^2-4ac}$

4.极限 \lim\limits

$\lim\limits_{n→∞}$

$\underset{n\to \infty }{\lim }$

$\lim\limits_{n\rightarrow+\infty}\dfrac{1}{n(n+1)}$

$\underset{n\to +\infty }{\lim }\frac{1}{n(n+1)}$

极限换行：\atop

$\lim\limits_{x→x_0\atop y→y_0}$

$\underset{\genfrac{}{}{0ex}{}{x\to x_0}{y\to y_0}}{\lim }$

5.积分 \int_下限^上限

一重积分号 \int

1.定积分：

$\int_0^1x^2{\rm d}x$

${\int }_0^1{x}^2\mathrm{d}x$

2.一重广义积分

$\int_{-∞}^{+∞}x^2{\rm d}x$

${\int }_{-\infty }^{+\infty }{x}^2\mathrm{d}x$

3.二重广义积分

$\int_{-∞}^{+∞}\int_{-∞}^{+∞}f(x,y){\rm d}x{\rm d}y$ 

${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(x,y)\mathrm{d}x\mathrm{d}y$

二重积分号 \iint

$\iint$

$\iint$

$\iint\limits_D$

$\underset{D}{\iint }$

三重积分号 \iiint

$\iiint$

$\iiint$

封闭积分 \oint

$\oint$

$\oint$

$\oiint$

$\iint$

积分号变大

\displaystyle

6.累加、累乘

累加 \sum

$\sum _{i=1}^n\frac{1}{x^2}$:$\sum\limits_{i=1}^n\dfrac{1}{x^2}$

累乘 \prod\limits

$\prod\limits_{i=0}^n$

$\prod _{i=0}^n$

 $\prod\limits_{i=0}^n\dfrac{1}{x_i^2}$

$\prod _{i=0}^n\frac{1}{x_i^2}$

7.戴帽符号 \hat{}、\bar{}

$\hat{y}$ :$\hat{y}$
$\check{y}$:$\check{y}$
$\bar{s}$ ：$\bar{s}$

8.等价符号：\Leftrightarrow

$\Leftrightarrow$

$\iff$

9.长横线、取非 \overline{}

$\overline{CF+OF}=1$

$\overline{CF+OF}=1$

10.箭头上写字 \xrightarrow[]{}

1.单向箭头

$A \xleftarrow{n=0} B \xrightarrow[T]{n>0} C$

$A\stackrel{n=0}{\leftarrow }B\underset{T}{\overset{n>0}{\to }}C$

2.双向箭头

$\xleftrightarrow[1]{2}$

$\underset{1}{\overset{2}{\leftrightarrow }}$

3.箭头长度可变的双向箭头

$罗尔定理 \underset{特例}{\xrightleftharpoons{推广}} 拉格朗日中值定理\underset{特例}{\xrightleftharpoons{推广}}柯西中值定理$

$罗尔定理\underset{特例}{\stackrel{推广}{\rightleftharpoons }}拉格朗日中值定理\underset{特例}{\stackrel{推广}{\rightleftharpoons }}柯西中值定理$

11.等号上写字 \xlongequal[]{}

 $$\oiint\limits_Σ|y|\ {\rm d}S\xlongequal{轮换对称性}\dfrac{1}{3}\oiint\limits_Σ(|x|+|y|+|z|)\ {\rm d}S$$

$$\underset{\Sigma }{\iint }|y|\mathrm{d}S\stackrel{轮换对称性}{=}\frac{1}{3}\underset{\Sigma }{\iint }(|x|+|y|+|z|)\mathrm{d}S$$

13.绝对值：\lvert 内容 \rvert

 $\lvert X-Y\rvert$

$|X-Y|$

用Latex代码写绝对值主要是为了在CSDN表格中使用绝对值。如果直接用键盘上的 | 符号，会和CSDN的表格构造冲突。

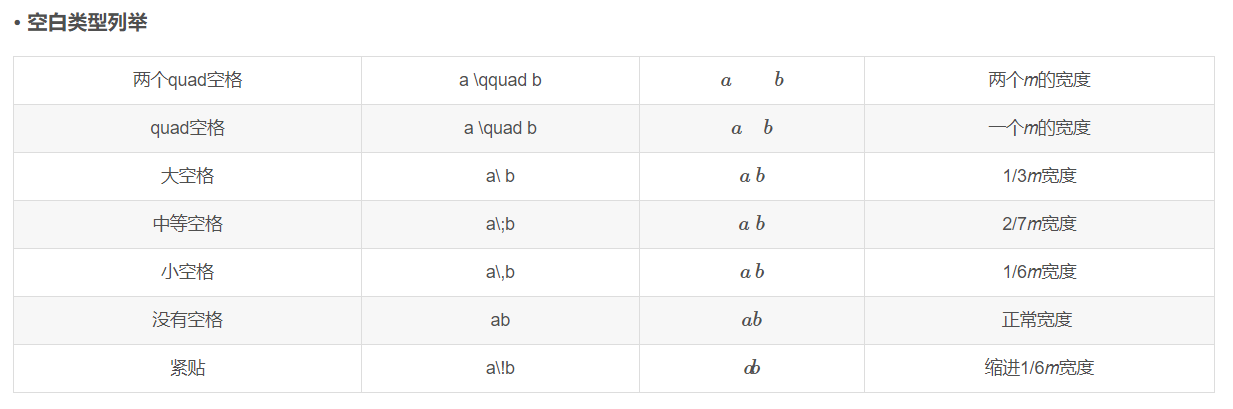
14.空格

\quad和 \qquad

15.矢量 \vec{}

$\vec{a}·\vec{c}$

$\vec{a}\cdot \vec{c}$

16.列向量 \binom{}{}

$\binom{n}{m}$    

$\left(\genfrac{}{}{0ex}{}{n}{m}\right)$

$\dbinom{n}{m}$     //同样可以加d放大

$\left(\genfrac{}{}{0ex}{}{n}{m}\right)$

$\left(\begin{array}{c}x_1 \\ x_2 \\x_3 \\x_4\end{array}\right)$

$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)$

17.矩阵

$\left(\begin{array}{cc}x_1 & x_2 \\ x_3 & x_4 \end{array}\right)$

$\left(\begin{array}{cc}{x}_1& x_2\\ x_3& x_4\end{array}\right)$

\left(\begin{array}{cc}a₁₁ & a₁₂ & a₁₃  \\ a₂₁ & a₂₂ & a₂₃  \\a₃₁ & a₃₂ & a₃₃  \\		\end{array}\right)

$\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)$

\left(\begin{array}{cc}λ₁ &      &   \\ & λ₂  &    \\&      & λ₃\\		\end{array}\right)

$\left(\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & {\lambda }_3\end{array}\right)$

\left(\begin{array}{cc}λ₁ &      &   \\ & λ₂  &    \\&      & ...\\&&&	λ_n		\end{array}\right)

$\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ...& \\ & & & {\lambda }_n\end{array}\right)$

分块矩阵

$A=\left[\begin{array}{cc}B& O\\ O& C\end{array}\right]$

18.行列式

只需要把矩阵的( )、[ ] 换成| |

$\left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\ \frac{∂}{∂x} & \frac{∂}{∂y} & \frac{∂}{∂z}\\P&Q&R \end{array}\right|$

$\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ P& Q& R\end{array}\right|$

$\left|\begin{array}{cc}O & B \\ A & C \end{array}\right|=\left|\begin{array}{cc}C & B \\ A & O \end{array}\right|=(-1)^{mn}|A||B|$

$\left|\begin{array}{cc}O& B\\ A& C\end{array}\right|=\left|\begin{array}{cc}C& B\\ A& O\end{array}\right|=(-1{)}^{mn}|A||B|$

19.大括号

$\left\{\begin{aligned}
x & =  φ(t) \\
y & =  ψ(t) 
\end{aligned}\right.$

示例1：
$\{\begin{array}{rl}x& =\phi (t)\\ y& =\psi (t)\end{array}$

示例2：

$$f(x)=\left\{\begin{aligned}
x & =  \cos(t) \\
y & =  \sin(t) \\
z & =  \frac xy
\end{aligned}\right.$$

$$f(x)=\{\begin{array}{rl}x& =\cos (t)\\ y& =\sin (t)\\ z& =\frac{x}{y}\end{array}$$

示例3：

$$E(X)=\left\{\begin{aligned}
\sum\limits_{k=1}^∞x_kp_k \qquad&\quad ，离散型 \\
\int_0^{+∞}xf(x)dx &\quad ，连续型 
\end{aligned}\right.$$

$$E(X)=\{\begin{array}{rl}\sum _{k=1}^{\infty }{x}_k{p}_k& ，离散型\\ {\int }_0^{+\infty }xf(x)dx& ，连续型\end{array}$$

20.方程组

$$\begin{cases}
a_1x+b_1y+c_1z=d_1 \\ 
a_2x+b_2y+c_2z=d_2 \\ 
a_3x+b_3y+c_3z=d_3
\end{cases}$$

$$\{\begin{array}{l}{a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\\ a_{3}x+b_{3}y+c_{3}z=d_3\end{array}$$

21.排列组合

排列

$C_n^k$ 

C斜体：$C_n^k$

${\rm C}_n^k$   

C正体：${\mathrm{C}}_n^k$

$\complement_n^k$

${\complement }_n^k$

组合

$A_n^k$

A斜体：$A_n^k$

${\rm A}_n^k$    

A正体：${\mathrm{A}}_n^k$

22.相似 ~   \sim

$A\sim B$

$A\sim B$

23.卡方分布 \chi^2

$\chi^2$

${\chi }^2$

24.包含于

1.包含于：
A ⊂ B
\subset

2.包含：
B ⊃ A
\supset

3.真包含于：
A ⊆ B
\subseteq

4.真包含：
B ⊇ A
\supseteq

25.各种箭头

推导箭头：$\Rightarrow$

Latex各种箭头

26.转义字符:大括号{ }   { }

$\{$

{ \{ {

调整

1.让字母变大：\frac改为\dfrac
2.积分变正体：\rm
3.累加、累乘上下限不写在后边，强制写在上边：\limits
4.块公式$$ 公式$$之间调整行距：\\[5mm]

---

原来：每行都用块公式，导致间隔很大

$$e^x=\sum\limits_{n=0}^∞\dfrac{1}{n!}x^n \qquad (-∞<x<+∞)$$
$$\dfrac{1}{1-x}=\sum\limits_{n=0}^∞x^n \qquad (-1<x<1)$$
$$\dfrac{1}{1+x}=\sum\limits_{n=0}^∞(-x)^n=\sum\limits_{n=0}^∞(-1)^nx^n \qquad (-1<x<1)$$

$$e^x=\sum _{n=0}^{\infty }\frac{1}{n!}{x}^n(-\infty <x<+\infty )$$
$$\frac{1}{1-x}=\sum _{n=0}^{\infty }{x}^n(-1<x<1)$$
$$\frac{1}{1+x}=\sum _{n=0}^{\infty }(-x{)}^n=\sum _{n=0}^{\infty }(-1{)}^n{x}^n(-1<x<1)$$

调整后：只用一个块公式，换行用 \\[5mm]

$$e^x=\sum\limits_{n=0}^∞\dfrac{1}{n!}x^n \qquad (-∞<x<+∞) \\ [5mm]
\dfrac{1}{1-x}=\sum\limits_{n=0}^∞x^n \qquad (-1<x<1)\\[5mm]
\dfrac{1}{1+x}=\sum\limits_{n=0}^∞(-x)^n=\sum\limits_{n=0}^∞(-1)^nx^n \qquad (-1<x<1)$$

$$\begin{gathered} e^x=\sum _{n=0}^{\infty }\frac{1}{n!}{x}^n(-\infty <x<+\infty ) \\ [5mm]\frac{1}{1-x}=\sum _{n=0}^{\infty }{x}^n(-1<x<1) \\ \frac{1}{1+x}=\sum _{n=0}^{\infty }(-x{)}^n=\sum _{n=0}^{\infty }(-1{)}^n{x}^n(-1<x<1) \end{gathered}$$

---

参考来源：
https://blog.csdn.net/Anne033/article/details/124328566