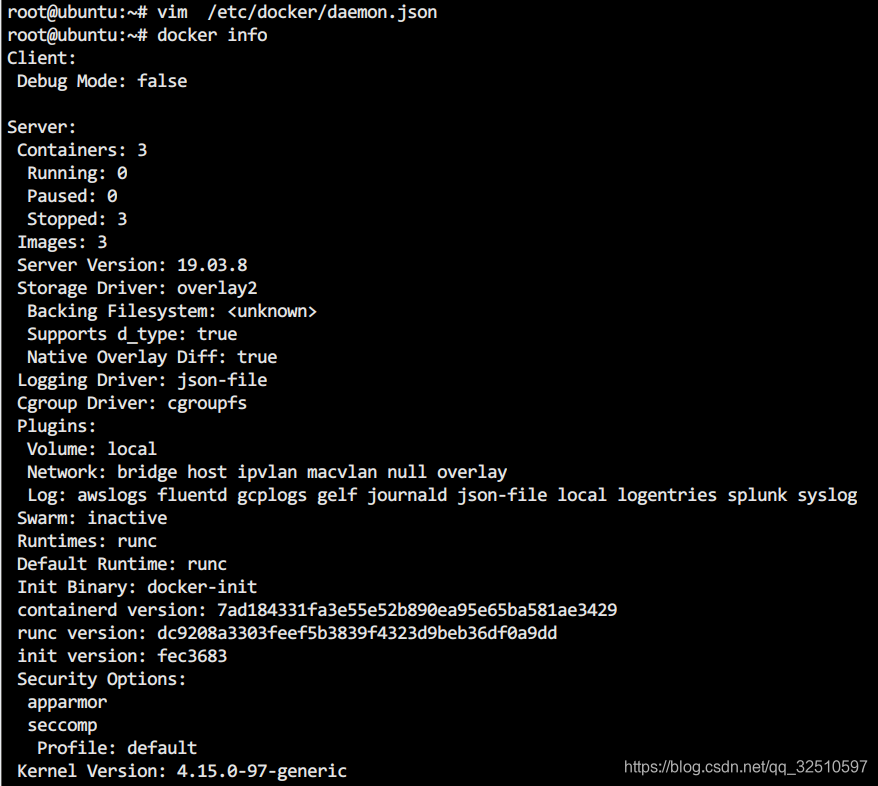
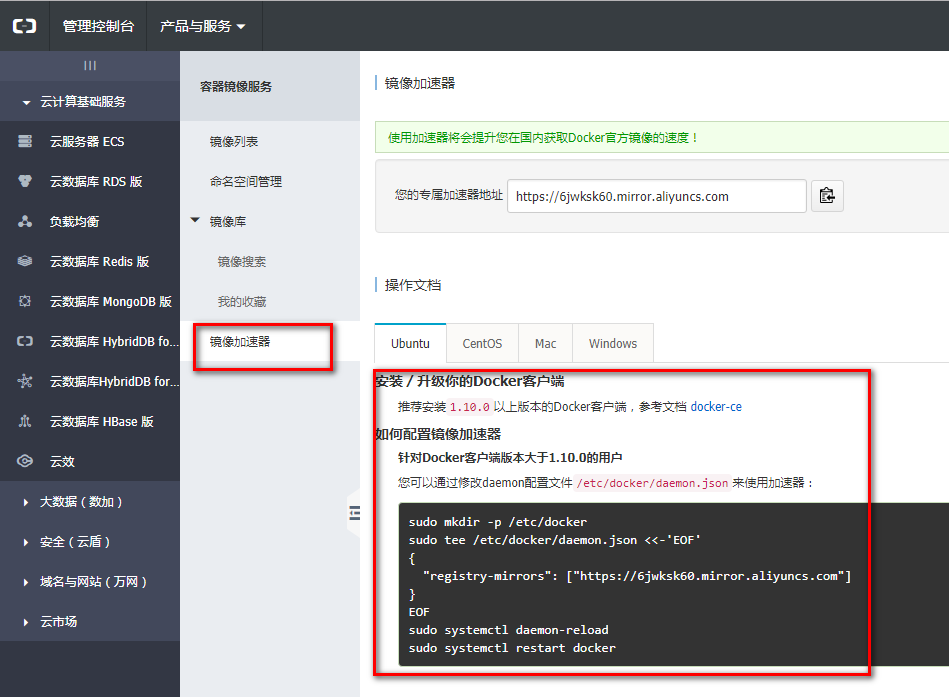
一、为何有skipList这种数据结构的出现

我们知道二分查找算法之所以能达到 O(logn) 这样高效的一个重要原因在于它所依赖的数据结构是数组，数组支持随机访问一个元素，通过下标很容易定位到中间元素。而链表是不支持随机访问的，只能从头到尾依次访问。但是数组有数组的局限性，比如需要连续的内存空间，插入删除操作会引起数组的扩容和元素移动，链表有链表的优势，链表不需要先申请连续的空间，插入删除操作的效率非常高。在很多情况下，数据是通过链表这种数据结构存储的，如果是有序链表，真的就没有办法使用二分查找算法了吗？实际上对有序链表稍加改造，我们就可以对链表进行二分查找。这就是我们要说的跳表。说到底，skipList的出现就是为了实现有序链表的二分查找，使有序链表的查找速度能够媲美它的效率和红黑树以及 AVL 树，而删除和插入的速度又能比他们速度更快。下面我们来看一下，跳表是怎么跳的。这里记住一句话：跳表的查找、插入、删除的时间复杂度都是 O(logn）

二、跳表的特点及结构

总结就是一句话：给有序的链表再加索引，在n级索引的基础上，还可以再加n+1级索引，直至该级索引的索引点只有2个时，就没必要再加索引

先看一下跳表的特点

1. 由很多层组成
2. 每一层都是一个有序链表
3. 最底层的链表包含所有元素
4. 每个元素插入时随机生成它的leve
5. 如果一个元素出现在第i层的链表中，则它在i-1层中也会出现
6. 上层节点可以跳转到下层
7. 跳表查询、插入、删除的时间复杂度为O(log n)，与平衡二叉树接近

跳表的最终结构图：

三、跳表相关操作

1. 查找操作，查找的时间复杂度
   
   查找元素的过程是从最高级索引开始，一层一层遍历最后下沉到原始链表。所以，时间复杂度 = 索引的高度 * 每层索引遍历元素的个数。

图中所示，现在到达第 k 级索引，我们发现要查找的元素 x 比 y 大比 z 小，所以，我们需要从 y 处下降到 k-1 级索引继续查找，k-1级索引中比 y 大比 z 小的只有一个 w，所以在 k-1 级索引中，我们遍历的元素最多就是 y、w、z，发现 x 比w大比 z 小之后，再下降到 k-2 级索引。所以，k-2 级索引最多遍历的元素为
w、u、z。其实每级索引都是类似的道理，每级索引中都是两个结点抽出一个结点作为上一级索引的结点。
现在我们得出结论：当每级索引都是两个结点抽出一个结点作为上一级索引的结点时，每一层最多遍历3个结点。
跳表的索引高度 h = log2n，且每层索引最多遍历 3 个元素。所以跳表中查找一个元素的时间复杂度为 O(3*logn)，省略常数即：O(logn)。

2. 空间复杂度

跳表通过建立索引，来提高查找元素的效率，就是典型的“空间换时间”的思想，所以在空间上做了一些牺牲，那空间复杂度到底是多少呢？

假如原始链表包含 n 个元素，则一级索引元素个数为 n/2、二级索引元素个数为 n/4、三级索引元素个数为 n/8 以此类推。所以，索引节点的总和是：n/2 + n/4 + n/8 + … + 8 + 4 + 2 = n-2，空间复杂度是 O(n)。
如下图所示：如果每三个结点抽一个结点做为索引，索引总和数就是 n/3 + n/9 + n/27 + … + 9 + 3 + 1= n/2，减少了一半。所以我们可以通过较少索引数来减少空间复杂度，但是相应的肯定会造成查找效率有一定下降，我们可以根据我们的应用场景来控制这个阈值，看我们更注重时间还是空间。

3. 插入数据

插入数据看起来也很简单，跳表的原始链表需要保持有序，所以我们会向查找元素一样，找到元素应该插入的位置。如下图所示，要插入数据6，整个过程类似于查找6，整个的查找路径为 1、1、1、4、4、5。查找到第底层原始链表的元素 5 时，发现 5 小于 6 但是后继节点 7 大于 6，所以应该把 6 插入到 5 之后 7 之前。整个时间复杂度为查找元素的时间复杂度 O(logn)。

这里有一个需要格外注意的地方：如果只是单纯插入数据而不更新索引，跳表最后也会退化成链表，如下图：

4. randomLevel() 方法

对于这个问题 ，可能大家普遍想到的方法就是，插入数据后删除原来的索引，再重新建立索引。那么重建索引的重建索引的时间复杂度是多少呢？因为索引的空间复杂度是 O(n)，即：索引节点的个数是 O(n) 级别，每次完全重新建一个 O(n) 级别的索引，时间复杂度也是 O(n) 。造成的后果是：为了维护索引，导致每次插入数据的时间复杂度变成了 O(n)。

那有没有其他效率比较高的方式来维护索引呢？假如跳表每一层的晋升概率是 1/2，最理想的索引就是在原始链表中每隔一个元素抽取一个元素做为一级索引。换种说法，我们在原始链表中随机的选 n/2 个元素做为一级索引是不是也能通过索引提高查找的效率呢？ 当然可以了，因为一般随机选的元素相对来说都是比较均匀的。如下图所示，随机选择了n/2 个元素做为一级索引，虽然不是每隔一个元素抽取一个，但是对于查找效率来讲，影响不大，比如我们想找元素 16，仍然可以通过一级索引，使得遍历路径较少了将近一半。如果抽取的一级索引的元素恰好是前一半的元素 1、3、4、5、7、8，那么查找效率确实没有提升，但是这样的概率太小了。我们可以认为：当原始链表中元素数量足够大，且抽取足够随机的话，我们得到的索引是均匀的。我们要清楚设计良好的数据结构都是为了应对大数据量的场景，如果原始链表只有 5 个元素，那么依次遍历 5 个元素也没有关系，因为数据量太少了。所以，我们可以维护一个这样的索引：随机选 n/2 个元素做为一级索引、随机选 n/4 个元素做为二级索引、随机选 n/8 个元素做为三级索引，依次类推，一直到最顶层索引。这里每层索引的元素个数已经确定，且每层索引元素选取的足够随机，所以可以通过索引来提升跳表的查找效率。

那代码该如何实现，才能使跳表满足上述这个样子呢？可以在每次新插入元素的时候，尽量让该元素有 1/2 的几率建立一级索引、1/4 的几率建立二级索引、1/8 的几率建立三级索引，以此类推，就能满足我们上面的条件。现在我们就需要一个概率算法帮我们把控这个 1/2、1/4、1/8 ... ，当每次有数据要插入时，先通过概率算法告诉我们这个元素需要插入到几级索引中，然后开始维护索引并把数据插入到原始链表中。下面开始讲解这个概率算法代码如何实现。
我们可以实现一个 randomLevel() 方法，该方法会随机生成 1~MAX_LEVEL 之间的数（MAX_LEVEL表示索引的最高层数），且该方法有 1/2 的概率返回 1、1/4 的概率返回 2、1/8的概率返回 3，以此类推。

1. randomLevel() 方法返回 1 表示当前插入的该元素不需要建索引，只需要存储数据到原始链表即可（概率 1/2）
2. randomLevel() 方法返回 2 表示当前插入的该元素需要建一级索引（概率 1/4）
3. randomLevel() 方法返回 3表示当前插入的该元素需要建二级索引（概率 1/8） randomLevel() 方法返回 4 表示当前插入的该元素需要建三级索引（概率1/16）
4. 。。。以此类推

所以，通过 randomLevel() 方法，我们可以控制整个跳表各级索引中元素的个数。重点来了：randomLevel() 方法返回 2 的时候会建立一级索引，我们想要一级索引中元素个数占原始数据的 1/2，但是 randomLevel() 方法返回 2 的概率为 1/4，那是不是有矛盾呢？明明说好的 1/2，结果一级索引元素个数怎么变成了原始链表的 1/4？我们先看下图，应该就明白了。

假设我们在插入元素 6 的时候，randomLevel() 方法返回 1，则我们不会为 6 建立索引。插入 7 的时候，randomLevel() 方法返回3 ，所以我们需要为元素 7 建立二级索引。这里我们发现了一个特点：当建立二级索引的时候，同时也会建立一级索引；当建立三级索引时，同时也会建立一级、二级索引。所以，一级索引中元素的个数等于 [ 原始链表元素个数 ] * [ randomLevel() 方法返回值 > 1 的概率 ]。因为 randomLevel() 方法返回值 > 1就会建索引，凡是建索引，无论几级索引必然有一级索引，所以一级索引中元素个数占原始数据个数的比率为 randomLevel() 方法返回值 > 1 的概率。那 randomLevel() 方法返回值 > 1 的概率是多少呢？因为 randomLevel() 方法随机生成 1~MAX_LEVEL 的数字，且 randomLevel() 方法返回值 1 的概率为 1/2，则 randomLevel() 方法返回值 > 1 的概率为 1 - 1/2 = 1/2。即通过上述流程实现了一级索引中元素个数占原始数据个数的 1/2。

同理，当 randomLevel() 方法返回值 > 2 时，会建立二级或二级以上索引，都会在二级索引中增加元素，因此二级索引中元素个数占原始数据的比率为 randomLevel() 方法返回值 > 2 的概率。 randomLevel() 方法返回值 > 2 的概率为 1 减去 randomLevel() = 1 或 =2 的概率，即 1 - 1/2 - 1/4 = 1/4。OK，达到了我们设计的目标：二级索引中元素个数占原始数据的 1/4。

以此类推，可以得出，遵守以下两个条件：

1. randomLevel() 方法，随机生成 1~MAX_LEVEL 之间的数（MAX_LEVEL表示索引的最高层数），且有 1/2的概率返回1、1/4的概率返回 2、1/8的概率返回 3 …
2. randomLevel() 方法返回 1 不建索引、返回2建一级索引、返回 3建二级索引、返回 4 建三级索引 …

就可以满足我们想要的结果，即：一级索引中元素个数应该占原始数据的 1/2，二级索引中元素个数占原始数据的 1/4，三级索引中元素个数占原始数据的 1/8 ，依次类推，一直到最顶层索引。

randomLevel() 方法代码：

// 理论来讲，一级索引中元素个数应该占原始数据的 50%，二级索引中元素个数占 25%，三级索引12.5% ，一直到最顶层。// 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点，都需要调用 randomLevel 生成一个合理的层数。// 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数，且 ：//        50%的概率返回 1//        25%的概率返回 2//      12.5%的概率返回 3 ...private int randomLevel() {int level = 1;while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {level += 1;}return level;}

完整的插入流程：

整个插入过程的路径与查找元素路径类似， 每层索引中插入元素的时间复杂度 O(1)，所以整个插入的时间复杂度是 O(logn)。

5. 删除数据
   
   删除元素的时间复杂度：
   删除元素的过程跟查找元素的过程类似，只不过在查找的路径上如果发现了要删除的元素 x，则执行删除操作。跳表中，每一层索引其实都是一个有序的单链表，单链表删除元素的时间复杂度为 O(1)，索引层数为 logn 表示最多需要删除 logn 个元素，所以删除元素的总时间包含 查找元素的时间 加 删除 logn个元素的时间 为 O(logn) + O(logn) = 2 O(logn)，忽略常数部分，删除元素的时间复杂度为 O(logn)。

本文转自