什么是类变量？

类变量也叫静态变量，静态属性，是该类所有对象共享的变量，任何一个该类的对象去访问他时，取到的值都是相同的值，同样任何一个该类对象 去修改他时，修改的也是同一个变量。

如何定义类变量？

访问修饰符 static 数据类型 变量名；
static 访问修饰符  数据类型 变量名；

如何访问类变量？

类名.类变量名 
或者
对象名.类变量名

测试代码1：

package com.hspedu.static_;public class StaticTest {public static void main(String[] args) {//测试访问类变量A a=new A();//对象访问System.out.println(a.count1);//结果是：100a.count1=20;//改变值//类名访问System.out.println(A.count1);//结果是：20System.out.println(A.count2);//结果是：200}}
class  A{//两种不同的创建类变量的方式static public int count1=100;public static int count2=200;
}

类变量的相关注意

1.什么时候需要用类变量
当我们需要让某个类的所有对象都共享一个变量时，就可以考虑使用类变量(静态变量):比如:定义职工类，统计所有职工共交多少钱。
2.类变量与实例变量(普通属性)区别
类变量是该类的所有对象共享的，而普通属性是每个对象独享的。
3.加上static称为类变量或静态变量，否则称为实例变量/普通变量/非静态变量
4.类变量可以通过类名.类变量名或者对象名.类变量名来访问，一般使用类名类变量名方式访问。要满足访问修饰符的访问权限和范围
5. 实例变量不能通过类名.类变量名方式访问。
6. 类变量是在类加载时就初始化了，也就是说，即使你没有创建对象，只要类加载了就可以使用类变量了。
7. 类变量的生命周期是随类的加载开始，随着类消亡而销毁。
测试代码2（注意事项第一点）当我们需要让某个类的所有对象都共享一个变量时，就可以考虑使用类变量(静态变量)：

package com.hspedu.static_;
public class Test2 {public static void main(String[] args) {//四个职工缴费Worker a=new Worker("王1炮",100);Worker b=new Worker("王2炮",500);Worker c=new Worker("王3炮",800);Worker d=new Worker("王4炮",200);//输出总金额System.out.println(Worker.Fee);//结果是：1600}}
class Worker{public static int  Fee=0;//静态变量public Worker(String name,int Fee){Worker.Fee+=Fee;}
}

测试代码3（注意事项第二点）：类变量是该类的所有对象共享的，而普通属性是每个对象独享的。

package com.hspedu.static_;public class Test3 {public static void main(String[] args) {System.out.println("没有修改的类变量值："+B.num1);//结果是：200//创建对象b1B b1 = new B();b1.num1=666;b1.num2=888;System.out.println("修改了的类变量值："+B.num1);//结果是：666System.out.println("对象b1的num2值："+b1.num2);//结果是：888//创建对象b2，验证类变量是否是共享，普通变量不是共享B b2 = new B();//看是否对象b1修改对对象b2有影响不System.out.println(b2.num1);//结果是：666System.out.println(b2.num2);//结果是：300}
}
class B{public static int num1=200;public int num2=300;
}

由此可证明：类变量是该类的所有对象共享的，而普通属性是每个对象独享的。

类方法基本介绍：

类方法也叫静态方法。
形式如下：
访问修饰符 static 数据返回类型 方法名（）{}
static 访问修饰符  数据返回类型 方法名（）{}

类方法的调用：

类名.类方法名 
或者
对象名.类方法名

测试代码4：

package com.hspedu.static_;public class Test4 {public static void main(String[] args) {//类名直接调用类方法System.out.println(C.way());C c = new C();//对象调用类方法System.out.println(c.way());//如果我们希望不创建实例，也可以调用某个方法(即当做工具来使用)// 这时，把方法做成静态方法时非常合适System.out.println(Math.abs(-63));//绝对值System.out.println(Math.sqrt(100));//开平方}
}
class C{public static int way(){return 1314520;}
}

小结：
当方法中不涉及到任何和对象相关的成员，则可以将方法设计成静态方法,提高开发效率。
比如:Math类、Arrays类、 Collections 集合类
实际开发，往往会将一些通用的方法，设计成静态方法，这样我们不需创建对象就可以使用，更加快捷

类方法使用注意事项和细节讨论

类方法和普通方法都是随着类的加载而加载，将结构信息存储在方法区:
类方法中无this的参数
普通方法中隐含着this的参数
2)类方法可以通过类名调用，也可以通过对象名调用
3)普通方法和对象有关，需要通过对象名调用，比如对象名.方法名(参数)，不能通过类名调用。
4)类方法中不允许使用和对象有关的关键字，比如this和super. 普通方法(成员方法)可以。
5)类方法(静态方法)中只能访问静态变量或静态方法。普通成员方法，既可以访问非静态成员，也可以访问静态成员。
小结: 静态方法，只能访问静态的成员,非静态的方法，可以访问静态成员和非静态成员(必须遵守访问权限)
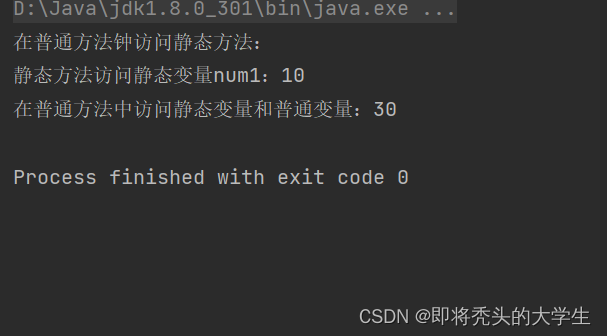
测试代码5类方法注意事项:

package com.hspedu.static_;package com.hspedu.static_;public class Test5 {public static void main(String[] args) {D d = new D();d.way2();//非静态方法，不能通过类名调用}
}
class D{public static int num1=10;public int num2=20;public static void way1(){//静态方法,类方法//类方法中不允许使用和对象有关的关键字，// 比如 this 和 super。普通方法(成员方法)可以//System.out.println(this.num1);报错//类方法(静态方法)中 只能访问 静态变量 或静态方法//System.out.println(way2());报错,访问非静态方法System.out.println("静态方法访问静态变量num1："+num1);;//若是num2+num1,num2报错因为不是类变量}public  void way2(){//非静态方法,普通方法// 非静态方法可以访问 静态成员和非静态成员System.out.println("在普通方法钟访问静态方法：");way1();System.out.println("在普通方法中访问静态变量和普通变量："+(this.num2+num1));}}

测试代码5运行结果：