这道题目编的比较好，第一问就构造的特别巧妙

（1） f(x)' = f‘(1)e^(x-1) - f(0) + x                                          f'(1) = f'(1) - f(0) + 1,        f(0)=1       

         f(x) = f'(1)e^(x-1) - f(0)x + 1/2x^2                                 f(0) = f'(1) e^(-1)               f'(1) = e

这里是比较奇怪的，因为这道题目的约束条件是x，但是求的最值是(a+1)b, 这道题目的正常做法就是由不等式关系恒成立，推出a和b必须满足的条件，然后再来求(a+1)b的最值，这样有点模糊。但幸好f(x)的形式比较简单。

f(x)= e^x - (a+1)x - b >=0  求(a+1)b的最大值。 这里想到规范化的技巧能够减小计算量令k=a+1

f(x)= e^x - kx-b >=0, 求kb的最大值。

f‘(x) = e^x -k ,    当k<0 时，f'(x) > 0 f(x)>=f(0)>=0     =>b>=0

当k>0时，f(x)>=f(ln(k)) = k-klnk-b>=0

上面的题目等价于k-klnk>=b时，求bk的最大值

bk<=k^2-k^2ln(k)

令f(k)=k^2-k^2ln(k)

这道题目其实是用极值点防缩，然后巧妙的实现了消元，其中第二步依赖于b刚好可以消元。

 

已知b-k+klnk<=0, 求-bk的最小值，可以尝试用拉格朗日数乘法+KKT条件做

构造L(b，k） = -(bk) + λ(b-k+klnk)

L对b求导  -k + λ = 0,  λ=k

L对k求导  -b + λ(-1+1+lnk)=0        -b + λln(k)=0    

两个等式解得  kln(k) = b           2klnk - k =0， 解得k=0，或者k=exp(1/2)   b=exp(1/2)*1/2, 

bk的最大值时exp(1)/2， 容易严重满足KKT条件

 

实际上，这道题目一上来直接套用凸优化的拉格朗日乘数法+KKT条件也是可以做出来的，其中关于x的偏导数为0的方程就是第一个部消去的步骤。

 

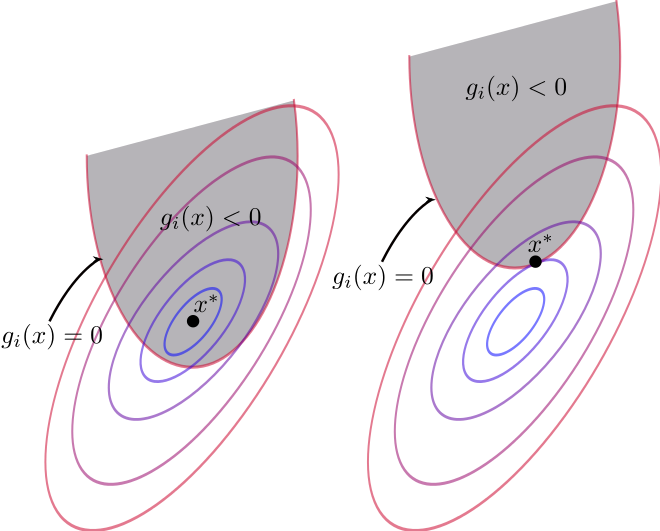
这道题目还可以用几何意义做出来，这也是拉格朗日乘数法和KKT条件的几何意义。

 

 

 

 

附录KKT条件的结论。