以二维空间 R^2 举例

1. 无约束的优化问题
   
   注意我在图里画了等高线。此时 在局部极小值点 处的梯度必然为0，比较容易理解。这个梯度为零的条件是局部极小值点的必要条件。这样，优化问题的求解变成了对该必要条件解方程组。

2.带等式约束的优化问题,

与无约束的问题不同。我们所要求的极小值点被限制在曲线 上，我们将 称为可行域, 解只能在这个可行域里取。如下图所示，曲线 （黑色实曲线）经过无约束极小值点（黑点）附近。那么满足约束的极小值点应该与黑点尽可能近。我们将 的等高线不断放大，直到与曲线 相切，切点即为所求。相切是关键，是极小值点的必要条件。

把 沿着曲线方向参数化为 , 。必有 在红点 的梯度方向与 的切线方向垂直，即另外，由于 为常数，那么也有复合函数 , 因此 在 t 的导数必为0，根据链式法则有 （内积为0，说明 与 垂直）因为 垂直于 ， 垂直于 ，所以 与 共线，有 若为最小值点就必须满足上式和问题中的约束 ,这个必要条件就叫作拉格朗日条件，为了好记，定义一个拉格朗日函数令其偏导为0，正好就得到拉格朗日条件。如此，带等式约束的优化问题转化为了无约束的优化问题，只需要对拉格朗日条件解方程组即可。这里λ就是拉格朗日乘子，有多少个等式约束就有多少个拉格朗日乘子。

3. 带不等式约束的优化问题
   
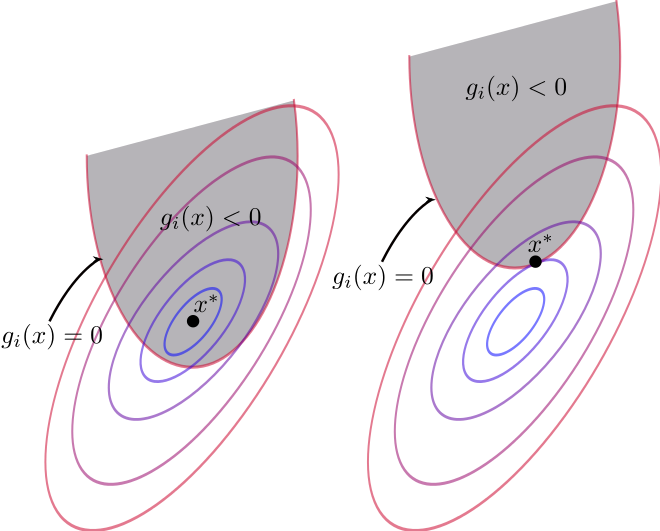
   当只有一个不等式起作用时, 如我们把问题2里的等式约束 h(x)=0 改为 h(x) \leq 0 ，如下图所示，可行域变成了阴影部分，最小值点还是切点，情况和问题2完全一样，只需要把不等号当做等号去求解即可。

当两个不等式起作用时，那么问题就来了 , s.t. , . 如下图，当 的等高线慢慢扩大时，等高线与可行域(阴影部分)第一次相遇的点是个顶点，2个不等式同时起作用了。满足约束的最小值点从原来的黑点位置(切点)移动到了红点位置，现在跟哪条约束函数曲线都不相切。这时候就需要用到kkt条件了。这里的“条件”是指：某一个点它如果是最小值点的话，就必须满足这个条件（在含不等式约束的优化问题里）。这是个必要条件，前面说的也全部是必要条件。

这个问题的解 应满足的KKT（卡罗需-库恩-塔克）条件为： 1. ， ; 2. ; 3. .其中，μ叫KKT乘子，有多少个不等式约束就有多少个KKT乘子。加上问题3中的约束部分，就是完整版的KKT条件。对于有等式的情况，你把其中一个不等式约束换成等式，可行域变成了半条曲线，最小值点还是那个红点，和下面这种情况是一样的。下面看看KKT条件是怎么来的。在问题2中我们知道了约束曲线的梯度方向与曲线垂直，我在上图画出了两条约束曲线的负梯度方向（绿色箭头）和等高线的梯度方向（红色箭头）。如果这个顶点是满足约束的最小值点，那么该点处（红点），红色箭头一定在两个绿色箭头之间( 方向一定指向 减小的方向，即 的那一边)。即 能被 和 线性表出（ ），且系数必非负（ ， ）。也就是kkt条件中的1和21. ， ; 2. .有时候，有的不等式约束实际上不起作用，如下面这个优化问题 , s.t. ; ; .如下图的 是不起作用的

对于最小值点 ,三个不等式约束的不同在于 （起作用） （起作用） （不起作用, 最小值点不在 上）这时，这个问题的KKT条件1，2成了：1. ， ， ; 2. . 条件2中的 这一项让我们很苦恼啊， 的绿色箭头跟我们的红色箭头没关系。要是能令 就好了。加上条件3：3. 恰好能使 。由于 ， ，所以前两项等于0，第三项 , 在条件3的作用下使得 . 正好满足需求。如果再多几项不起作用的不等式约束，比如 。要使就只能有 同样地， , , 只能出现 或者 和 异号的情况。但注意条件1限制了 ， ，所以只能有 。因此不管加了几个不起作用的不等式约束，条件2都能完美实现：目标函数 的梯度 被起作用的不等式约束函数 的负梯度（ ）线性表出且系数 全部非负（红色箭头被绿色箭头夹在中间）。这样，优化问题的求解就变成对所有KKT条件解方程组。如果再定义一个拉格朗日函数令它对x的偏导为0，就是KKT条件中的条件2了。最后说明一下，以上所有都是局部极小值点的必要条件。据此求得的解不一定是局部极小值点（更别提全局了），原因是上图中我所画的等高线也许根本就不闭合，也就是说我们一直想要靠近的等高线中间的黑点压根就是个鞍点或者近似鞍点！