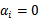在最优化问题中，经常是会有约束条件的，而约束条件可分为等式约束条件和不等式约束条件，对于前者，我们有拉格朗日乘子法，对于后者，有KKT条件，对于既有等式约束又有不等式约束的最优化问题，只需要结合拉格朗日乘子法和KKT条件即可。本文中，我们将分别看下等式约束和不等式约束下，拉格朗日乘子法和KKT条件的原理，以及如何去理解。

       其实只要理解了等式约束条件下的拉格朗日乘子法，那么理解KKT条件就简单多了，因此我们先讲一下应该如何去理解拉格朗日乘子法。现假设有如下优化问题：

                       

其中f1和f2都是连续可微的函数。我们可以把这个问题画成如下的二维平面图，其中圆圈表示等高线，数字对应于函数f2的函数值，圆圈的形状就是当我们拿一个和xOy平行的平面在f2对应函数值的地方去截取到的交线。从图中可知，f2的形状就像一个碗。其中的曲线为函数f1(x,y)=0的图像，其就是约束条件。现在，上面的最优化问题等价于在图中曲线上找一点，使得其和函数值最小的等高线相切（这里不是相交，原因是如果相交，那么说明曲线贯穿了等高线，又因为函数是连续的，所以在交点邻域肯定存在更小的值）。所以若点x*是最优解，则x*所在的等高线必然是和约束曲线相切的。关键在于，怎么将这种几何关系表达出来呢？根据梯度的意义，我们自然就想到了用梯度去形式化表达这个问题。

       我们知道，梯度是多元函数的偏导组成的向量，其方向表示函数值增加最快的方向，而且，对于某一点，在该点的邻域内，只要沿着和该点梯度方向的夹角小于90度的方向变化，那么函数值一定是变大的，同理只要夹角大于90度，那么沿着这个方向，邻域内函数值一定是变小的，对于梯度的这些含义，还不理解的读者可以参考笔者之前写的一篇关于梯度的文章。由于沿着梯度方向变化，函数值增加最快，所以显然梯度方向必然是和该点对应的等高线垂直的，如图中A点箭头所示，和函数值为4对应的等高线垂直。因为前述中我们知道，在最优点，该点的等高线和约束曲线是相切的，所以该点对应的梯度也是和约束曲线垂直的，如图中B点的箭头所示，但是该箭头表示的是B点梯度的反方向。最后，对于约束曲线，我们可以认为其是函数f1(x,y)在函数值为0处的等高线，即把z=f1(x,y)也看做一个多元函数，那么在点B处，我们也可以求得其在函数f1上的梯度。所以，若点B是最优解，根据相切的性质，可知必有B在f1和f2上的梯度共线，这是B为最优解的一个必要条件，其形式化的表达为：

                         

其中倒三角表示梯度，lambda为一待求的未知变量。而这个实际上就是拉格朗日乘子法求导转化后的等价形式。当然，上述说明是在一个等式约束下的，如果是多个等式约束，我们可以用逐个添加等式约束的思路去分析，最终根据等价的传递性，可以得到多个等式约束下的拉格朗日乘子形式。其思路过程如下图所示。

       至此，我们已经从几何直观上推导出了拉格朗日乘子法的原理。接下来，我们再基于此讲一下在不等式约束下，KKT条件的推导。实际上，KKT条件对等式和不等式约束共存的系统下是通用的，但是这里我们先研究单纯的不等式约束下的KKT条件，然后稍加扩展就可以得到等式和不等式约束下的KKT条件。

       延续上述的例子，我们稍加改变，即把等式约束修改为f1(x,y)<=0,且假设曲线的左侧为约束域。这时，我们知道，最小值依然是在点B上，由于B同时也在f1(x,y)上，所以依然满足上述的梯度表达式，但是这时因为f1(x,y)的左侧才是小于0的约束域，所以我们知道B在f1(x,y)上的梯度方向肯定是垂直曲线向右的，所以这时两个梯度共线但是方向相反，所以lambda是小于0的，这时我们已经可以确定lambda的符号了。当然，也有可能约束域为曲线的右侧，这时最小值便不是B点了，而是可以更小，可能是函数本身的梯度为0处的极值点，而这时，最优解便不再约束域的边界上，而是在约束域的内部。如果最优解在约束域内部，那么此时如果我们依然想让梯度表达式成立，则必须让lambda为0，这样才能保证梯度表达式总是成立的（因为此时目标函数梯度为0，尽管约束函数在该点的梯度也可能为0，这时lambda不必为0，梯度表达式也成立，但是为了保证其总是成立，可以令此时的lambda总是为0，即当最优解不在约束域边界时，令lambda总是为0）。所以，上面的陈述被格式化表达之后，就成了KKT条件。即在让目标函数变成等式约束下的目标函数之后，还需要添加lambda*f1(x,y)=0这样的条件；此外，因为在不等式约束下，最大化或者最小化问题中，lambda的符号实际上是可以确定的，但是仅仅有lambda*f1(x,y)=0这个条件还无法保证lambda的符号，即可能会解出多个lambda，但是其中有些不符合符号要求的解是要被剔除的，比如这些解可能对应的不是极小值，而是极大值，所以我们还应该添加一个lambda的符号要求，即lambda>=0或者lambda<=0,这里到底是大于等于还是小于等于，需要视不等式约束的符号以及是最大化还是最小化的问题而定，这个只要理解了原理，便可以很快的判断出来lambda的符号约束。对于有多个不等式约束或者同时也有等式约束的最优化问题，同样可以根据单个约束条件进行扩展。

       以上就是关于拉格朗日乘子法和KKT条件的直观理解和推导，这里最后需要强调的是：1、这里的最优化问题分析的论述，始终是基于最优解邻域来得到结论的；2、始终只能找到局部最优解，是否是全局最优，需要视具体问题而定；3、这里无论是拉格朗日乘子法还是KKT条件，都是解的必要条件，我们都只是根据解的性质，来反推出其应该满足的性质，从而得到这些方法；4、推导KKT条件时，我们的思路是为了让其依然保持梯度等式的成立，然后进行lambda符号条件和lambda*f1(x,y)=0条件的添加，即后者条件的添加是为了让梯度等式始终保持成立，这样才能构成一个完整的必要条件；5、KKT条件其实还是不方便求解的，因此我们还可以进一步把KKT条件中的等号约束用拉格朗日乘子给消除掉，留下关于lambda的符号约束，并且可以先不管符号约束，求解出lambda，然后再利用符号约束进行过滤即可，这样求解比较方便。