拉格朗日乘子法的证明

在学习支持向量机的时候，计算对偶问题时用到了拉格朗日乘子法((Lagrange multiplier method))，回想起高中时使用拉格朗日乘子法求不等式约束条件下的最优化问题时的困惑，虽然一直知道用，但是却不知道为什么拉格朗日乘子法能够用。知其然更应知其所以然，本文就来扒一扒“拉格朗日乘子法”的来龙去脉。

等式约束下的最优化问题

给定一个不等式约束条件下的最优化问题，

$$\begin{array} {I}\mathop {\min }\limits_x \quad f(x) \\ s.t.\quad g(x) = 0\end{array}\quad\quad (1)$$

此处假定$f(x)$为凸函数，需要找到的是在约束条件$g(x)=0$的条件下，使得目标函数$f(x)$最小的$x$值(注：$x$为一个n维向量)。一般情况下，对于一个凸函数的极值问题，我们只需要找到令目标函数的梯度${\nabla_x^{'}}=0$的点$x$即可。然而，由于此处存在的等式约束条件,使得目标函数梯度等于0的点不一定能够满足约束条件。

从几何的角度看，这个问题的目标是在由方程$g(x)=0$所确定的$d-1$维曲面上，找到能使得目标函数$f(x)$最小化的$d$维点。我们以下图中二维空间为例：求函数$f(x,y)$在约束条件$g(x,y)=0$下的最小值。我们想象$f(x,y)$是一座“山”,$x$与$y$分别是其经纬度，$f(x,y)$为其海拔，图中的椭圆为这座”山”的等高线；约束条件$g(x,y)=0$为海拔为0的平面上的一条曲线。我们在这座”山”上乱逛，想要找到一个最高的点（最大与最小问题是相对的），但是我们的经纬度必须满足$g(x)=0$，即投影到海拔为0的平面上的话必须与图中红色曲线一致。

显然，如果我们找到了一个最高点，必然有最高点所在的等高线$f(x,y)=d_1$与约束曲线$g(x)=0$是相切的。否则，我必然还可以沿着红色的约束曲线继续走，找到一个更高的点（例如：图中红色曲线与登高线$f(x,y)=d_2$相交）。用数学语言描述相切便意味着，在极值点，有：$\nabla f(x) = \lambda *\nabla g(x)$，即两个函数在极值点的梯度向量是平行的。

这个时候我们引入拉格朗日函数：$L(x, \lambda) = f(x) + \lambda g(x)$， 其中，$\lambda$就是拉格朗日乘子，为一个未知常数。 在求该函数关于$x,\lambda$极值问题时有：

$$\begin{array}{I}{1}^{o}\quad \nabla_x L(x,\lambda) = \nabla f(x) - \lambda *\nabla g(x)=0 \\ 2^{o} \quad \nabla_{\lambda}L(x,\lambda) = g(x)=0\end{array} \qquad (2)$$

这意味着: 无约束条件下最小化拉格朗日函数$L(x,\lambda)$与有约束条件$g(x)=0$下原目标函数$f(x)$最小化的问题是一致的。求出令拉格朗日函数$L(x,\lambda)$最小的$(x,\lambda)$的值，便解出了原优化问题$(1)$的解，即我们将原优化问题$(1)$转换成了优化问题$(2)$：

$$\mathop{\min}\limits_{x, \lambda}L(x, \lambda) = f(x)+\lambda g(x) \qquad(3)$$

只要解除了$(2)$中线性方程组的解，那么便能够得到原目标函数的极值了。

不等式约束条件下的最优化问题

等式约束下的最优化的问题只是热热身，真正麻烦却也重要的，是不等式约束下的最优化问题。考虑将$(1)$中的问题进行推广，对最优化问题加上不等式约束：

$$\begin{array} {I}\mathop {\min }\limits_x \quad f(x) \\ s.t.\quad h(x) = 0\\ \qquad \ \ \ g(x) \le 0\end{array} \quad\quad (4)$$

仍然考虑向量$x$为二维空间中的点的场景，图中阴影部分为$g(x)<0$区域，椭圆线为”盆地”的登高线， 不等式约束意味着我们只能在阴影区域找”盆地”的最低点。此时可能存在两种情况：

1. “盆地“的中心在阴影部分区域，此时我们可以不用理会约束条件，直接求$f(x)$的极小值就行；
2. “盆地”的中心在阴影部分外面，此时在我们所能找到的极值点，必然有$g(x)=0$曲线与极值点的登高线相切，否则必然能够往阴影区域继续找到一个海拔更低的点。并且该极小值点关于约束函数的梯度$\nabla g(x)$与关于目标函数的梯度$\nabla f(x)$方向必定是相反的(不相反却相切的情况，只能是第一种，但那种情况的切点并不是极小值) 。

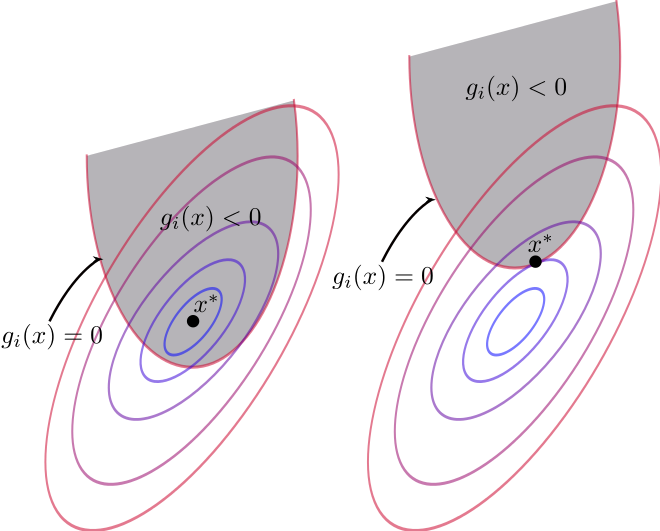
总结上面的情况，给出不等式约束条件下的库恩-塔克条件为：

$$\begin{array}{I}1^{o}\nabla_x L(x) = \nabla f(x) + \lambda*\nabla g(x) +u*\nabla h(x) = 0 \quad...相切\\ 2^{o} \nabla_u L(x) = h(x) = 0 \\ 3^{o} \nabla_ \lambda L(x) = g(x) \le 0 \\ 4^{o}\lambda \ge0 \\ 5^{o}u*g(x) = 0 \quad....要么相切g(x)=0,要么极大值与g(x)无关,\lambda=0\end{array}$$

对偶问题