对于只有等式约束的非线性优化问题，拉格朗日定理是可以适用的，但是当存在不等式约束时就不适用了，此时Karush–Kuhn–Tucker(KKT)条件是更为通用的处理技术，拉格朗日定理其实只是KKT条件定理的特殊情况。 KKT条件一开始称为Kuhn–Tucker条件, 因为在1951年Harold W. Kuhn 和 Albert W. Tucker发表了该定理的论文，不过人们之后又发现早在1939年一个名为William Karush的学者就在他的硕士论文中涉及了该理论，所以又把他的名字加入到了该定理的命名中。该定理名字里的"条件"的意思是这个定理描述的是最优解的必要条件，也就是是说如果一个解是优化问题的最优解，那么这个解一定满足KKT条件所叙述的各种关系；按照逻辑学的理论，原命题与逆否命题等价，那么如果一个解它不满足KKT条件，那么它肯定不是最优问题的最优解；当然，如果一个解满足KKT条件，我们不能直接说它就是最优解。

二元单约束的KKT条件

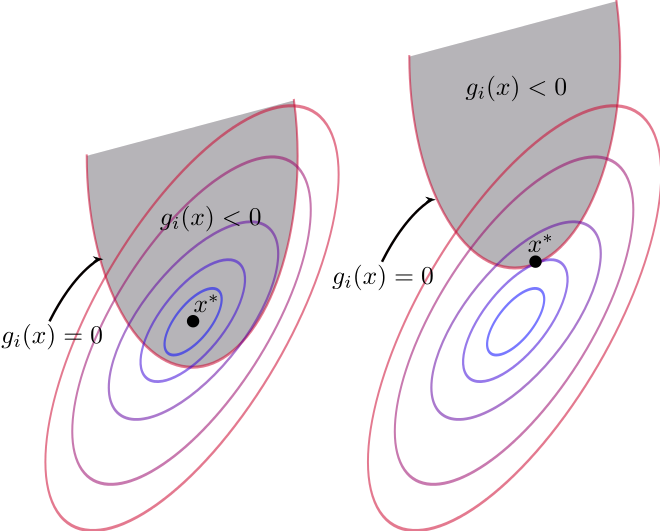
先通过一个最简单的二元单个约束的优化问题来得到它的KKT条件，然后给出扩展的一般性定理；二元单个约束方面图像描述，便于理解。问题的描述：
$$\begin{array}{rl}maximize& f(x_1,x_2)\\ subjectto& g(x_1,x_2)\le b\end{array}$$
如果约束是等式，可以直接应用拉格朗日定理来处理；但现在约束是不等式，无法直接应用拉格朗日定理，按照拉格朗日定理的描述，最优解是约束边界曲线与目标函数等值线的切点，但现在最优解可能出现在约束边界之内；这时我们可以这样考虑，最优解要么出现在约束区域的边界上，要么出现在边界之内，所以我们就分两种情况来分析：

情况一

先考虑最优解出现在约束边界上，那么这时原始问题就等价于：
$$\begin{array}{rl}maximize& f(x_1,x_2)\\ subjectto& g(x_1,x_2)=b\end{array}$$
就是只有等式约束的优化问题，自然这个问题可以直接应用拉格朗日定理来处理
$$\begin{array}{r}DL(x_1^{\ast },x_2^{\ast })=D(f(x_1^{\ast },x_2^{\ast })-\lambda g(x_1^{\ast },x_2^{\ast }))=Df(x_1^{\ast },x_2^{\ast })-\lambda Dg(x_1^{\ast },x_2^{\ast })=(0,0)\end{array}$$
可以想象其二维的图形分布如下图所示，其最优解出现在约束曲线与目标函数等值线相切的点

但是这时我们需要额外考虑的是$\lambda$的正负性，当原始问题是等式约束时是不需要考虑$\lambda$的正负的，但当原始问题是不等式约束时则必须要考虑。梯度的一个重要意义是它的方向是指向函数增长(正)最快的方向，对于上图中处于约束边界上的最优解的点，它在约束函数$g(x_1,x_2)-b$上的梯度$Dg(x_1^{\ast },x_2^{\ast })$应该是指向约束边界外围，因为在约束边界上$g(x_1^{\ast },x_2^{\ast })-b=0$，而约束外围则是$g(x_1^{\ast },x_2^{\ast })-b>0$，函数值是增大的：

再来考虑目标函数上的梯度$Df(x_1^{\ast },x_2^{\ast })$，它应该指向约束区域内部还是外部呢? 如果它指向约束内部，那么就意味着我们可以在约束内部找到一个更好的解，因为在约束内部的解是满足原始问题的约束的，同时它处于目标函数的梯度方向上，它的目标值也更大，这个结论将与我们的假设前提相悖；所以目标函数的梯度$Df(x_1^{\ast },x_2^{\ast })$必须也是指向约束区域外部的；所以$Df(x_1^{\ast },x_2^{\ast })$和$Dg(x_1^{\ast },x_2^{\ast })$应该是同向的，同向也就意味着$\lambda$必定是大于等于零的。

总结一下，当最优解出现在约束边界上时，最优解的必要条件是：
$$\begin{array}{r}\frac{\partial L}{\partial x_1^{\ast }}=\frac{\partial f}{\partial x_1^{\ast }}-\lambda \frac{\partial g}{\partial x_1^{\ast }}=0\\ \frac{\partial L}{\partial x_2^{\ast }}=\frac{\partial f}{\partial x_2^{\ast }}-\lambda \frac{\partial g}{\partial x_2^{\ast }}=0\\ g(x_1^{\ast },x_2^{\ast })=b\\ \lambda \ge 0\end{array}$$

情况二

再来考虑最优解出现在约束边界内即$g(x_1,x_2)<b$的情况。
当我们假设最优解就是出现在约束边界之内时，这个约束加不加其实不影响结果，原始问题就等价于无约束优化问题，它们的最终解是一样的：
$$\begin{array}{rl}maximize& f(x_1,x_2)\\ subjectto& g(x_1,x_2)<b\end{array}⟺\begin{array}{rl}maximize& f(x_1,x_2)\end{array}$$
因为最优解就是无约束时的目标函数最优值，那么必然满足
$$Df(x_1^{\ast },x_2^{\ast })=(0,0)⟺\begin{array}{r}\frac{\partial f}{\partial x_1^{\ast }}=0\\ \frac{\partial f}{\partial x_2^{\ast }}=0\end{array}$$
那这时$\lambda$的值是如何呢? 它应该等于零，这个结论老实说我不太清楚严格的数学证明是如何的，我是这样简单理解的：因为无约束优化问题其实也可以写成等式约束形式，不过约束的系数是零：
$$\begin{array}{rl}maximize& f(x_1,x_2)\\ subjectto& g^{\prime }(x_1,x_2)=0\ast g(x_1,x_2)=0\end{array}$$
把它化成拉格朗日函数:
$$L(x_1,x_2,{\lambda }^{\prime })=f(x_1,x_2)-{\lambda }^{\prime }{g}^{\prime }(x_1,x_2)=f(x_1,x_2)-({\lambda }^{\prime }\ast 0)g(x_1,x_2)$$
它也就是原问题(指的是约束只有$<$号的问题模型)的拉格朗日函数，所以原问题的$\lambda$就等于零，并且原问题对应的拉格朗日函数也满足：
$$\begin{array}{r}DL(x_1^{\ast },x_2^{\ast })=D(f(x_1^{\ast },x_2^{\ast })-\lambda g(x_1^{\ast },x_2^{\ast }))=Df(x_1^{\ast },x_2^{\ast })=(0,0)\end{array}$$
总结一下，当最优解出现在约束边界之内时，满足：
$$\begin{array}{r}\frac{\partial L}{\partial x_1^{\ast }}=\frac{\partial f}{\partial x_1^{\ast }}-\lambda \frac{\partial g}{\partial x_1^{\ast }}=0\\ \frac{\partial L}{\partial x_2^{\ast }}=\frac{\partial f}{\partial x_2^{\ast }}-\lambda \frac{\partial g}{\partial x_2^{\ast }}=0\\ g(x_1^{\ast },x_2^{\ast })<b\\ \lambda =0\end{array}$$

汇总

两种情况的结论其实差异之处就在于要么是$g(x_1^{\ast },x_2^{\ast })=b$，要么是$\lambda =0$，可以用一个等式来描述：
$$\lambda [g(x_1,x_2)-b]=0$$
这个等式一般称之为互补松弛条件(complementary slackness condition)

现在，我们可以给出二元单约束情况下的KKT条件：

• 假设$f$和$g$都是$C^1$(一阶可导)函数，$(x_1^{\ast },x_2^{\ast })$是函数$f$在约束集 { ( x 1 , x 2 ) ∈ R 2 : g ( x 1 , x 2 ) ≤ b } \{(x_1,x_2)\in \mathbb{R}^2: g(x_1,x_2)\leq b\} {(x1​,x2​)∈R2:g(x1​,x2​)≤b}下的最优解，并且满足$\frac{\partial g}{\partial x_1^{\ast }}\ne 0or\frac{\partial g}{\partial x_2^{\ast }}\ne 0$ ， 那么一定存在${\lambda }^{\ast }$使得以下关系成立:
  $$\begin{array}{rl}Df(x_1^{\ast },x_2^{\ast })-{\lambda }^{\ast }Dg(x_1^{\ast },x_2^{\ast })& =(0,0)\\ {\lambda }^{\ast }& \ge 0\\ {\lambda }^{\ast }[g(x_1^{\ast },x_2^{\ast })-b]& =0\end{array}$$

一般性的KKT条件

完整的KKT条件我直接从资料中摘录，当然证明过程就忽略，只记录下结论。为了定理的叙述，先明确一些定义：

• 定义一般性的优化问题为：
  m a x x { f ( x : x ∈ U ) } w h e r e : U = { x ∈ R n : g 1 ( x ) ≤ b 1 , . . . , g k ( x ) ≤ b k } \begin{aligned} &max_\mathtt{x}\{f(\mathtt{x}:\mathtt{x}\in U)\} \\ where:&U=\{\mathtt{x}\in \mathbb{R}^n : g_1({\mathtt{x}})\leq b_1,...,g_k({\mathtt{x}})\leq b_k \} \\ \end{aligned} where:​maxx​{f(x:x∈U)}U={x∈Rn:g1​(x)≤b1​,...,gk​(x)≤bk​}​
• 对于某一个不等式约束$g_i(\mathtt{x})\le b_i$，如果一个可行解${\mathtt{x}}^{\prime }$ 正好满足$g_i(\mathtt{x})=b_i$时称该约束是激活的(binding)，反之称之为未激活(not binding)
• 引入乘子${\lambda }_1,{\lambda }_2,...,{\lambda }_k$，构成拉格朗日函数：
  $$L(\mathtt{x},\lambda )=f(\mathtt{x})-{\lambda }_1[g_1(\mathtt{x})-b_1]-...-{\lambda }_k[g_k(\mathtt{x})-b_k]$$
• 对于某个可行解${\mathtt{x}}^{\prime }$，我们假设前面$e$个约束对于它是激活的，剩余的$k-e$个约束是未激活的；这$e$个激活约束可以构成一个雅可比矩阵：
  $$D{\mathtt{g}}_e(\mathtt{x})=\left[\begin{array}{ccc}\frac{\partial g_1}{\partial x_1}& \cdots & \frac{\partial g_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial g_e}{\partial x_1}& \cdots & \frac{\partial g_e}{\partial x_n}\end{array}\right]$$
  如果$D{\mathtt{g}}_e({\mathtt{x}}^{\prime })$是满秩矩阵(秩等于$e$)，那么称该可行解${\mathtt{x}}^{\prime }$满足NDCQ条件

然后我们有完整的KKT条件定理：

• $f,g_1,...,g_k$是$C^1$函数(一阶偏导)，如果${\mathtt{x}}^{\ast }$是优化问题的最优解，并且满足NDCQ条件，那么一定存在乘子${\lambda }_1,{\lambda }_2,...,{\lambda }_k$使得下面的关系成立:
  $$\begin{array}{r}Df({\mathtt{x}}^{\ast })-\sum _{i=1}^k{\lambda }_i^{\ast }D{g}_i({\mathtt{x}}^{\ast })=(0,...,0)\\ {\lambda }_1^{\ast }\ge 0,...,{\lambda }_k^{\ast }\ge 0\\ {\lambda }_1^{\ast }[g_1({\mathtt{x}}^{\ast })-b_1]=0,...,{\lambda }_k^{\ast }[g_k({\mathtt{x}}^{\ast })-b_k]=0\end{array}$$