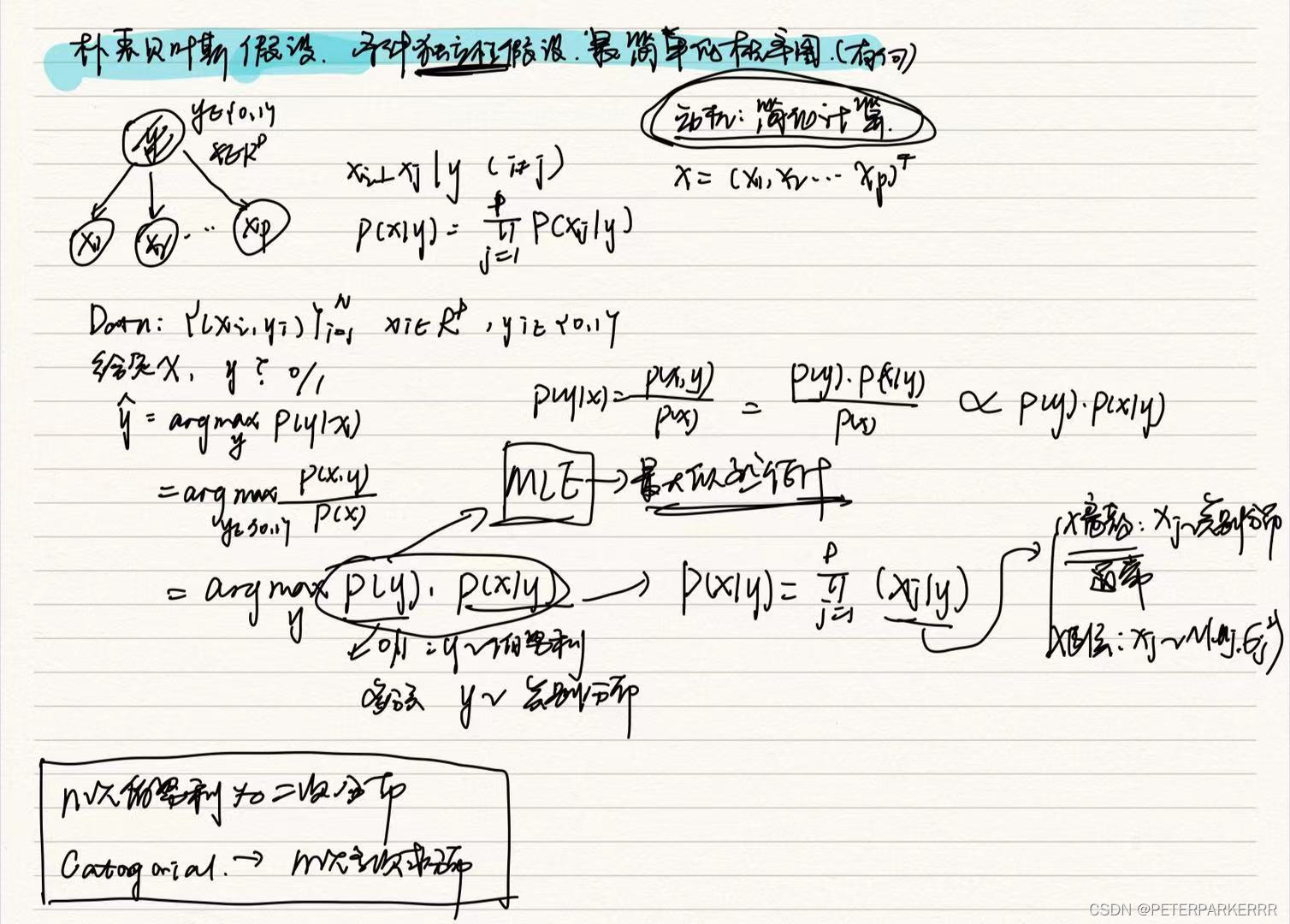
下表为训练数据集，特征向量只有一维，根据此数据表建立回归决策树。

在本数据集中，只有一个特征变量，最优切分变量自然是x。接下来考虑9个切分点{1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5}，根据下式计算每个待切分点的损失函数值：


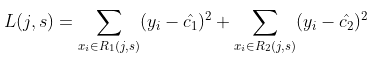
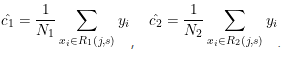
当切分点s=1.5时，可得c1和c2值

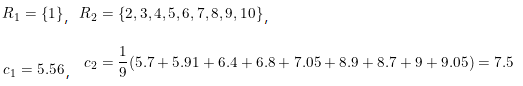
同理，其他切分点的c1和c2值如下

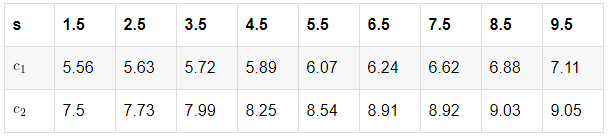
当切分点s=1.5时，可得损失函数值

同理，其他切分点的损失函数值如下

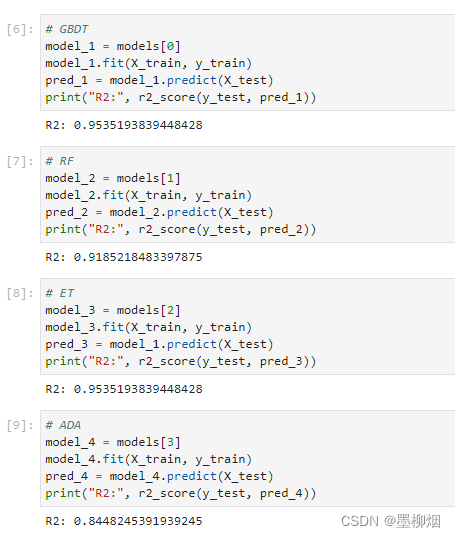
由上可知，当切分点s=6.5时，损失函数值最小。因此，第一个划分点为(j=x,s=6.5)，这是决策树的第一层，划分后可得：

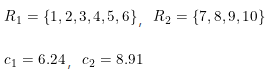
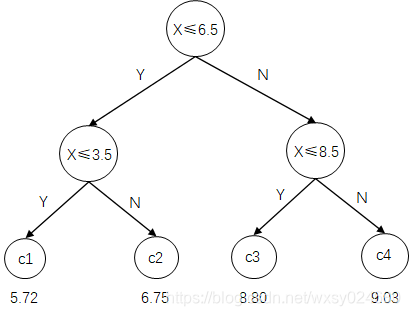
同理，我们进行第二层切分，经计算R1最佳切分点为3.5，R2最佳切分点为8.5，最终决策树如下图所示

代码实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree, linear_modelx = np.arange(1,11,1).reshape(-1,1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])# Fit regression model
model1 = tree.DecisionTreeRegressor(max_depth=2)
model2 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)# Predict
# X_test = np.arange(0.0, 12.0, 0.01)[:, np.newaxis]
X_test = np.arange(0.0, 12.0, 0.01).reshape(-1,1)
y1 = model1.predict(X_test)
y2 = model2.predict(X_test)# Plot the results
fig, axs = plt.subplots(1,1)
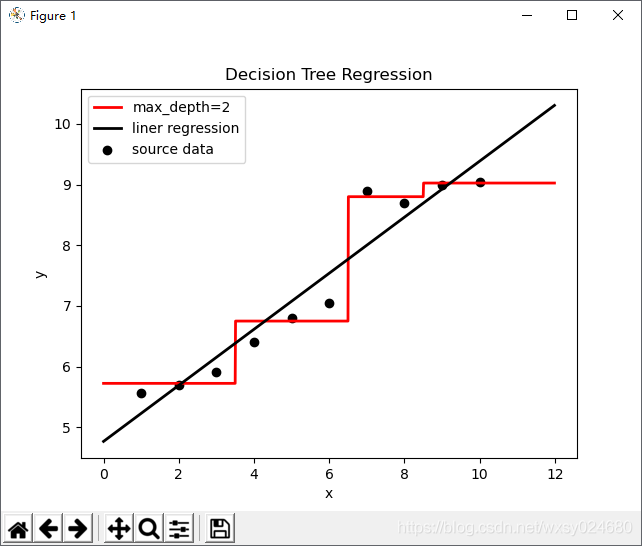
axs.scatter(x, y, color="black", label="source data")
axs.plot(X_test, y1, color="red", label="max_depth=2", linewidth=2)
axs.plot(X_test, y2, color='black', label='liner regression', linewidth=2)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

运行结果：