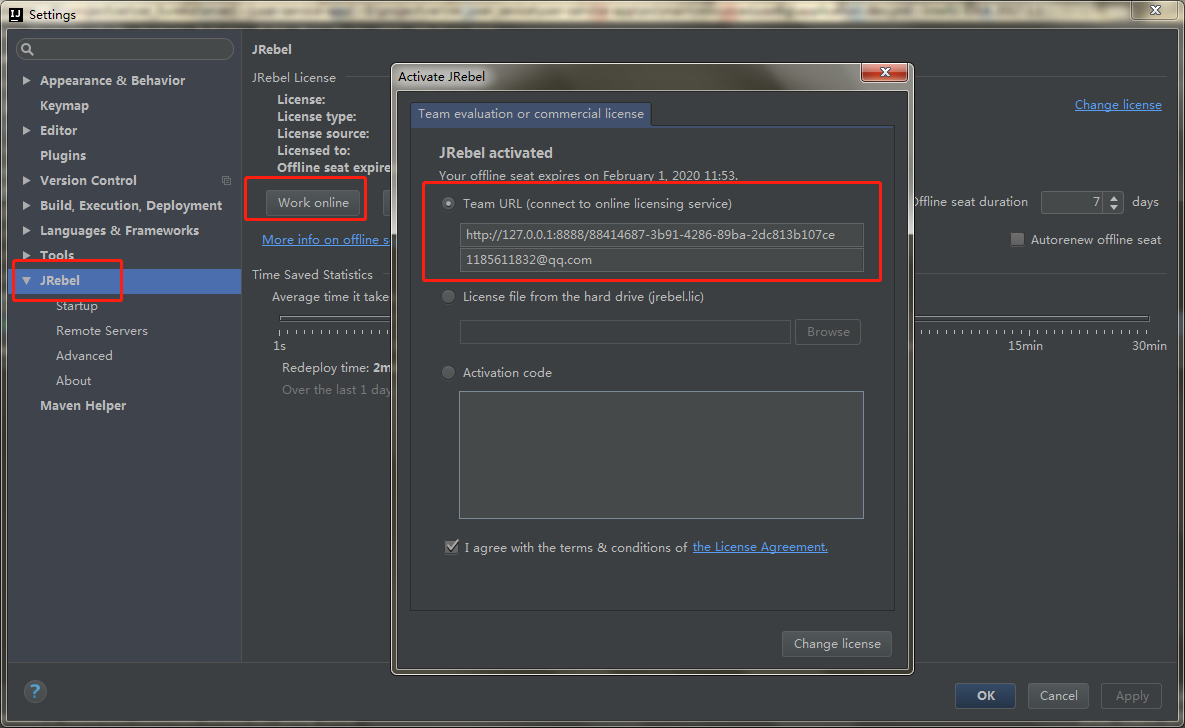
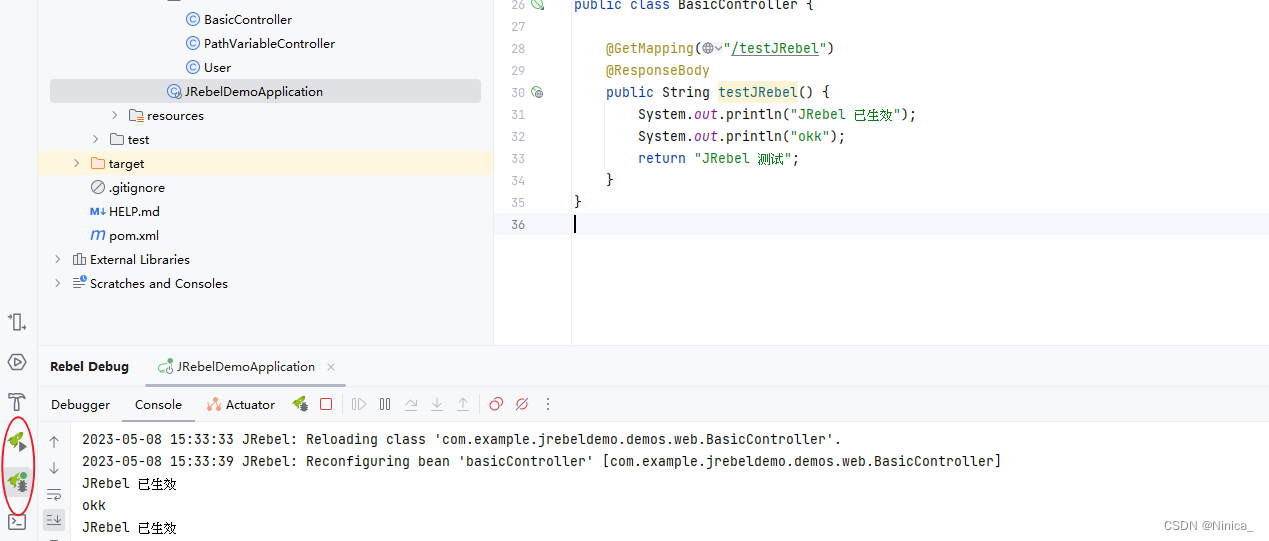
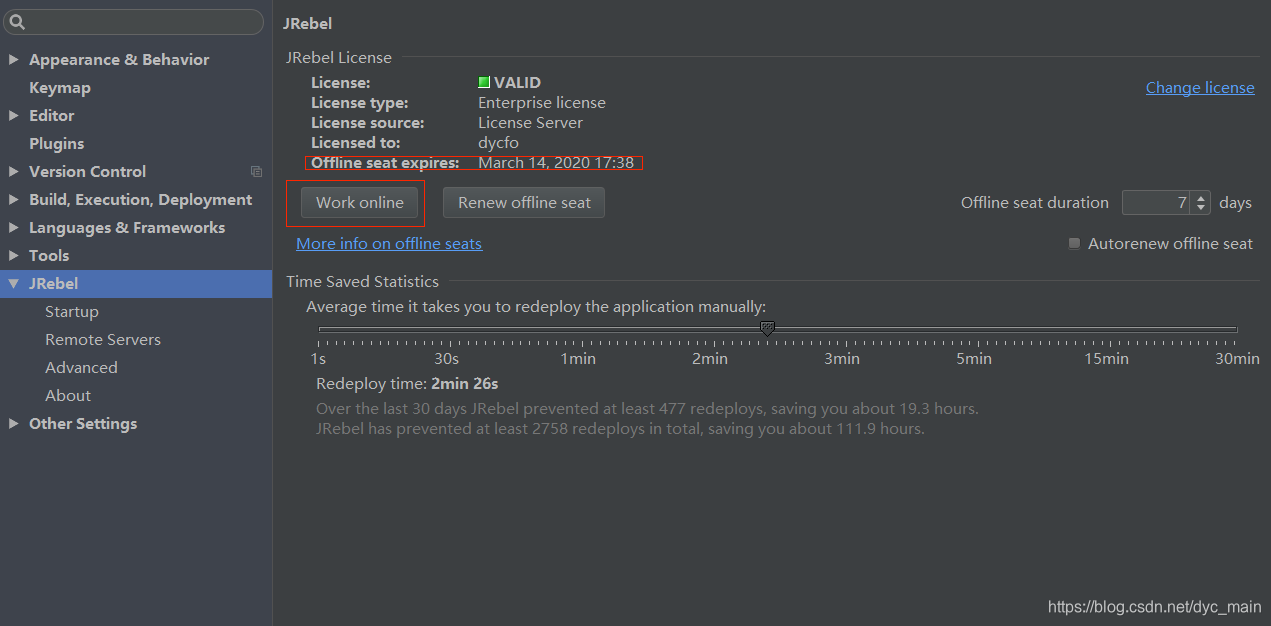
1. 回归问题

Given a labeled training set learn a general mapping which associates previously unseen independent test data with their correct continuous prediction.

回归问题和分类问题很相似，区别在于回归问题的输出是一个连续值。

上图是训练数据 和 对应的连续值的一个实例。训练数据用黑色点表示，数据对应的连续值由它在y轴上的位置体现。这个例子中，输入是一维的：x是自变量，y是因变量。
图中灰色点表示的是一个没有在训练数据中出现的数据，回归任务的目标就是根据训练数据得到自变量和因变量之间的关系。得到这个关系之后，对于没有出现在训练集中的数据，可根据其自变量，估计其因变量的值。

2. 一般步骤

要寻找数据和对应连续值之间的关系，实际就是要找到一个函数，能够将数据映射到连续值上。

回归问题一般通过以下三步解决：
1. Model: function set
选择一个模型。模型实际就是函数的集合，线性回归模型，就是所有线性函数组成的集合
2. Goodness of function
需要有一个评判标准，能够判断函数的好坏
3. Best function
利用上一步中评判标准，在函数集合中找到最好的函数

对于不同的模型，寻找最好的函数的方法，很有可能是不一样的。但是对于同一个问题，判断函数好坏的方法往往是相同的

3. Goodness of function

评价函数好坏的函数称作loss function(损失函数)，一般loss function的值越大，该函数表现得越差
它由loss term(损失项)和regularizerm(正则化项)两项相加构成：
1. loss term反映的是预测值与实际值之间的误差。对于回归问题，常用的loss term是均方误差
2. regularizer反映的是函数的复杂程度，函数越复杂，该项的值越大。

3.1. regularizer

正则化项是为了控制函数的复杂程度，它的思想符合奥卡姆剃刀原理：

在所有可能选择的函数中，能够很好地解释已知数据并且十分简单才是最好的函数

参数向量的范数是一种常用的正则化项：

$$L_1 = ||w||_1 = \sum _{i=1} ^{n} |w_i|\\ L_2 = ||w||_2 = \sqrt { \sum _{i=1} ^{n} {|w_i|^2} }$$
以 $L_1$范数为例，参数的绝对值之和越小，正则化项越小，函数越简单。极端情况，某个 $w_i$为0时，相当于某个参数没有作用。

4. Model & Best function

4.1. 线性回归模型

线性回归模型，表示的是线性函数的集合，$y = w^Tx +b$。其中x和y都是向量。

4.1.1. 最小二乘法

当loss function为均方误差时，用最小二乘法可以直接计算出$w$和$b$的解析解。

最小二乘法找到的是误差平方和最小的函数：

$$L = \sum _{i=1} ^{N} (\hat y_i - (w^T x_i + b))^2$$
这里 $\hat y_i$表示的实际值， $N$是样本个数

最小二乘法实际是对$w$和 $b$分别求偏导，令导数等于0