回归问题评价指标

article/2025/9/27 0:37:28

平均绝对值误差（MAE）

均方误差（MSE）

均方根误差（RMSE）

平均绝对百分比误差(MAPE)

均方误差对数(MSLE)

中位绝对误差(MedAE)

R Squared

总结

回归模型： $n$ 个样本，每个样本为 $(x_{i},y_{i})$ ，预测值为 $\hat{y_{i}}$ ， $i\in{1,2,\cdots ,n}$ .

平均绝对值误差（MAE）

计算每一个样本的预测值和真实值的差的绝对值，然后求和再取平均值。这个指标是对绝对误差损失的预期值。MAE对极端值比较敏感，即MAE 对异常值更加稳健，因为它不使用平方。

$MAE=\frac{1}{n}\sum_{i=1}^{n}|y_{i}-\hat{y_{i}}|$

#公式法
MAE_1 = np.mean(abs(y_test - prediction))
print(MAE_1)#使用sklearn.metrics模块
from sklearn.metrics import mean_absolute_error
MAE_2 = mean_absolute_error(y_test,prediction)
print(MAE_2)

均方误差（MSE）

（Mean Squared Error）计算每一个样本的预测值与真实值差的平方，然后求和再取平均值。该指标对应于平方(二次)误差的期望。是线性回归的损失函数，在线性回归的时候我们的目的就是让这个损失函数最小。受到异常值的影响很大。

$MSE=\frac{1}{n}\sum_{i=1}^{n}{(y_{i}-\hat{y_{i}})}^{2}$

#公式法
MSE_1 = np.mean((y_test - prediction)**2)
print(MSE_1)#使用sklearn.metrics模块
from sklearn.metrics import mean_squared_error
MSE_2 = mean_squared_error(y_test,prediction)
print(MSE_2)

均方根误差（RMSE）

（Root Mean Squard Error）均方根误差就是在均方误差的基础上再开方。该指标对应于平方(二次)误差的期望。受到异常值的影响很大，使用时应先剔除异常值。

$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(y_{i}-\hat{y_{i}})}^{2}}$

#公式法
RMSE_1 = np.sqrt(np.mean((y_test - prediction)**2))
print(RMSE_1)#使用sklearn.metrics模块:sklearn.metrics模块中没有直接计算均方根误差的函数，所以需要先计算均方误差，然后再开根号。
from sklearn.metrics import mean_squared_error
RMSE_2 = np.sqrt(mean_squared_error(y_test,prediction))
print(RMSE_2)

平均绝对百分比误差(MAPE)

（Mean Absolute Percentage Error）这个指标是对相对误差损失的预期值。所谓相对误差，就是绝对误差和真值的百分比。

$MAPE=\frac{1}{n}\sum_{i=1}^{n}\frac{||y_{i}-\hat{y_{i}}||}{||y_{i}||}$

均方误差对数(MSLE)

（Mean Squared Log Error）该指标对应平方对数(二次)差的预期。当数据当中有少量的值和真实值差值较大的时候，使用log函数能够减少这些值对于整体误差的影响。

$MSLE=\frac{1}{n}\sum_{i=1}^{n}{(log(1+y_{i})-log(1+\hat{y_{i}}))}^{2}$

中位绝对误差(MedAE)

（Median Absolute Error）通过取目标和预测之间的所有绝对差值的中值来计算损失。

$MedAE=median(|y_{1}-\hat{y_{1}}|,\dots,|y_{n}-\hat{y_{n}}|)$

R Squared

又叫可决系数(coefficient of determination)/拟合优度，取值范围为0~1，反映的是自变量 $x$ 对因变量 $y$ 的变动的解释的程度。越接近于1，说明模型拟合得越好。

$R^{2}=1-\frac{MSE(y,\hat{y})}{Var(y))}=1-\frac{\sum_{i=1}^{n}{(y_{i}-\hat{y_{i}})}^{2}}{\sum_{i=1}^{n}{(y_{i}-\bar{y}})^{2}}=\frac{SSE}{SST}=1-\frac{SSR}{SST}$

其中，

$SST={\sum_{i=1}^{n}{(y_{i}-\bar{y}})^{2}$ 表示的是 $y$ 的变动的程度，正比于方差；

$SSR={\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}$ 表示的是模型和真实值的残差；

$SSE={\sum_{i=1}^{n}(\hat{y_{i}}-\bar{y})^{2}$ 表示的是模型对 $y$ 的变动的预测。

$SST=SSR+SSE$ .

#公式法
R_1 = 1 - np.mean((y_test - prediction)**2)/np.mean((y_test - np.mean(y_test)**2))
print(R_1)#使用sklearn.metrics模块
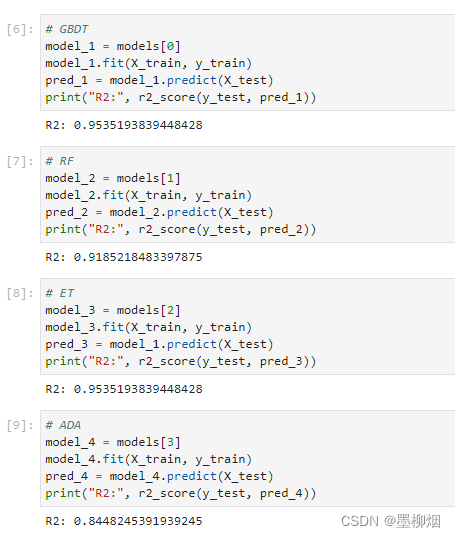
from sklearn.metrics import r2_score
R_2 = r2_score(y_test,prediction)
print(R_2)

总结

MAE、MSE、RMSE等可以准确的计算出预测结果和真实的结果的误差大小，均是越小越好，但却无法衡量模型的好坏程度。但是这些指标可以指导我们的模型改进工作，如调参、特征选择等。
$R^{2}$ 的结果可以很清楚的说明模型的好坏，越大越好。
MAE和RMSE一起使用，可以看出样本误差的离散程度。比如RMSE远大于MAE时，可以得知不同样例的误差差别很大。
MAE和MAPE一起使用，再结合 $\bar{y}$ ，可以估算模型对不同数量级样例的拟合程度。比如MAE远大于 $MAPE*\bar{y}$ 则可能是模型对真实值小的样本预测更准。可以考虑为不同数量级的样本建立不同的模型。