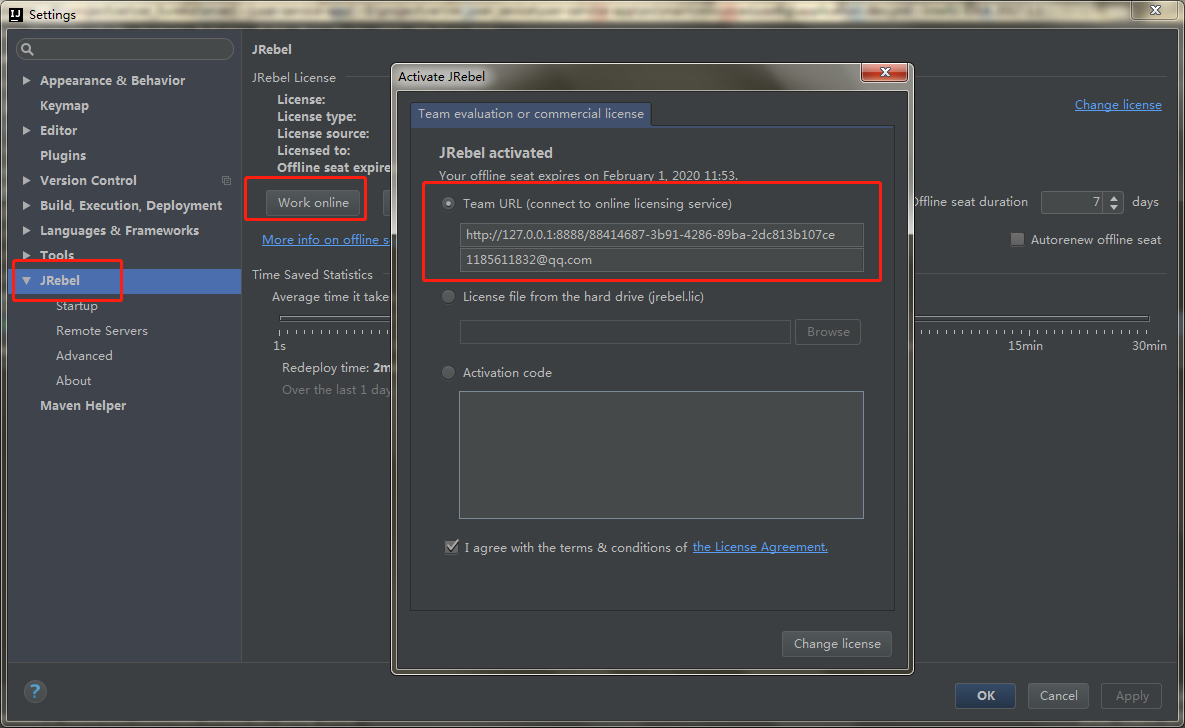
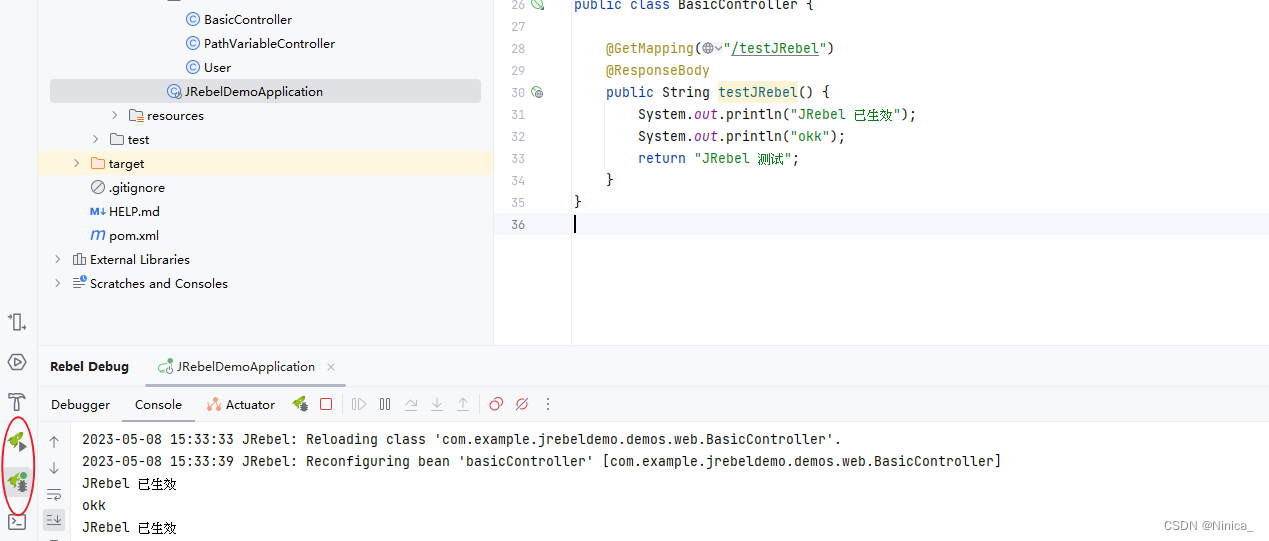
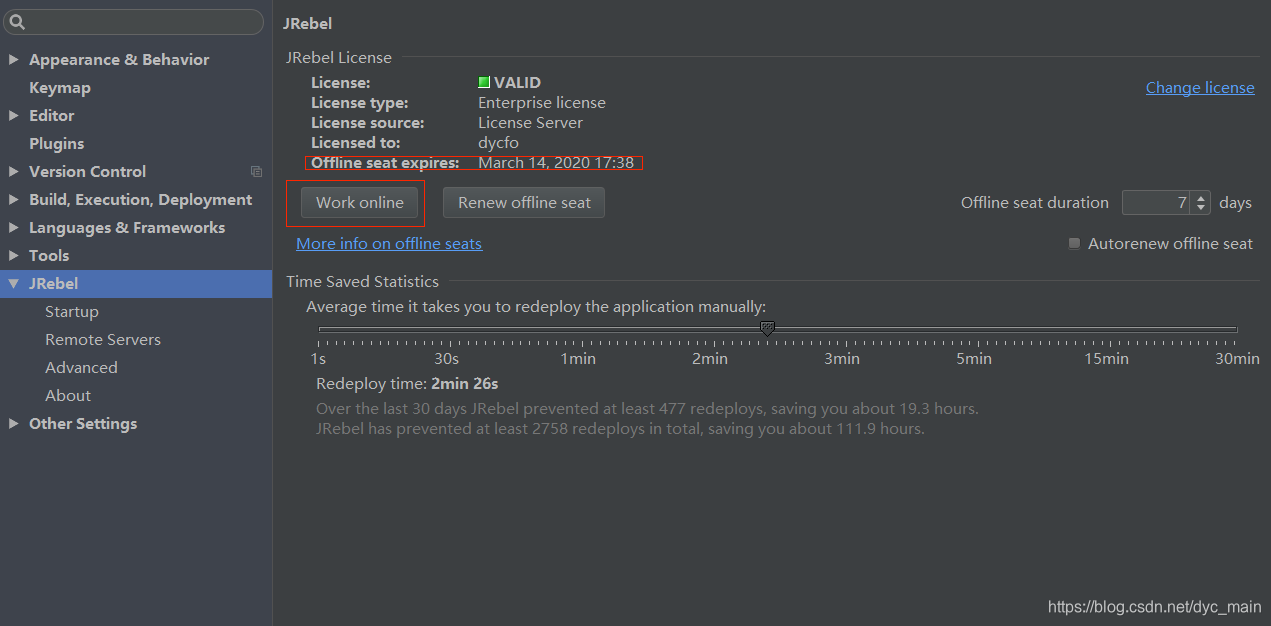
回归问题的条件/前提:
1) 收集的数据
2) 假设的模型,即一个函数,这个函数里含有未知的参数,通过学习,可以估计出参数。然后利用这个模型去预测/分类新的数据。
1. 线性回归
假设 特征 和 结果 都满足线性。即不大于一次方。这个是针对 收集的数据而言。
收集的数据中,每一个分量,就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数,向量表示形式:
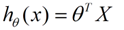
这个就是一个组合问题,已知一些数据,如何求里面的未知参数,给出一个最优解。 一个线性矩阵方程,直接求解,很可能无法直接求解。有唯一解的数据集,微乎其微。
基本上都是解不存在的超定方程组。因此,需要退一步,将参数求解问题,转化为求最小误差问题,求出一个最接近的解,这就是一个松弛求解。
求一个最接近解,直观上,就能想到,误差最小的表达形式。仍然是一个含未知参数的线性模型,一堆观测数据,其模型与数据的误差最小的形式,模型与数据差的平方和最小:
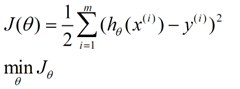
这就是损失函数的来源。接下来,就是求解这个函数的方法,有最小二乘法,梯度下降法。
http://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E6%96%B9%E7%A8%8B%E7%BB%84
最小二乘法
是一个直接的数学求解公式,不过它要求X是列满秩的,
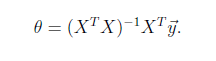
梯度下降法
分别有梯度下降法,批梯度下降法,增量梯度下降。本质上,都是偏导数,步长/最佳学习率,更新,收敛的问题。这个算法只是最优化原理中的一个普通的方法,可以结合最优化原理来学,就容易理解了。
2. 逻辑回归
逻辑回归与线性回归的联系、异同?
逻辑回归的模型 是一个非线性模型,sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函数关系,其他的步骤,算法都是线性回归的。可以说,逻辑回归,都是以线性回归为理论支持的。
只不过,线性模型,无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
另外它的推导含义:仍然与线性回归的最大似然估计推导相同,最大似然函数连续积(这里的分布,可以使伯努利分布,或泊松分布等其他分布形式),求导,得损失函数。
![\begin{align}J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^m y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) \right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/f/a/6/fa6565f1e7b91831e306ec404ccc1156.png)
逻辑回归函数
 表现了0,1分类的形式。
表现了0,1分类的形式。
应用举例:
是否垃圾邮件分类?
是否肿瘤、癌症诊断?
是否金融欺诈?
3. 一般线性回归
线性回归 是以 高斯分布 为误差分析模型; 逻辑回归 采用的是 伯努利分布 分析误差。
而高斯分布、伯努利分布、贝塔分布、迪特里特分布,都属于指数分布。
![]()
而一般线性回归,在x条件下,y的概率分布 p(y|x) 就是指 指数分布.
经历最大似然估计的推导,就能导出一般线性回归的 误差分析模型(最小化误差模型)。
softmax回归就是 一般线性回归的一个例子。
有监督学习回归,针对多类问题(逻辑回归,解决的是二类划分问题),如数字字符的分类问题,0-9,10个数字,y值有10个可能性。
而这种可能的分布,是一种指数分布。而且所有可能的和 为1,则对于一个输入的结果,其结果可表示为:
-
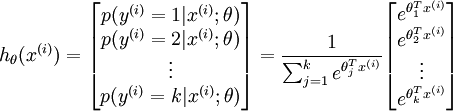 参数是一个k维的向量。
参数是一个k维的向量。
而代价函数:![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
而对于softmax的求解,没有闭式解法(高阶多项方程组求解),仍用梯度下降法,或L-BFGS求解。
当k=2时,softmax退化为逻辑回归,这也能反映softmax回归是逻辑回归的推广。
线性回归,逻辑回归,softmax回归 三者联系,需要反复回味,想的多了,理解就能深入了。
4. 拟合:拟合模型/函数
由测量的数据,估计一个假定的模型/函数。如何拟合,拟合的模型是否合适?可分为以下三类
合适拟合
欠拟合
过拟合
看过一篇文章(附录)的图示,理解起来很不错:
欠拟合:
合适的拟合
过拟合
过拟合的问题如何解决?
问题起源?模型太复杂,参数过多,特征数目过多。
方法: 1) 减少特征的数量,有人工选择,或者采用模型选择算法
http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html (特征选择算法的综述)
2) 正则化,即保留所有特征,但降低参数的值的影响。正则化的优点是,特征很多时,每个特征都会有一个合适的影响因子。
5. 概率解释:线性回归中为什么选用平方和作为误差函数?
假设模型结果与测量值 误差满足,均值为0的高斯分布,即正态分布。这个假设是靠谱的,符合一般客观统计规律。
数据x与y的条件概率:
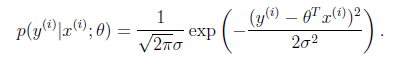
若使 模型与测量数据最接近,那么其概率积就最大。概率积,就是概率密度函数的连续积,这样,就形成了一个最大似然函数估计 。对最大似然函数估计进行推导,就得出了求导后结果: 平方和最小公式
。对最大似然函数估计进行推导,就得出了求导后结果: 平方和最小公式
6. 参数估计 与 数据的关系
拟合关系
7. 错误函数/代价函数/损失函数:
线性回归中采用平方和的形式,一般都是由模型条件概率的最大似然函数 概率积最大值,求导,推导出来的。
统计学中,损失函数一般有以下几种:
1) 0-1损失函数
L(Y,f(X