内容介绍

老生常谈的话题分类问题和回归问题之间有一个重要的区别。从根本上说，分类是关于预测标签，回归是关于预测数量。

我经常看到这样的问题：

如何计算回归问题的准确度？

像这样的问题表明没有真正理解分类和回归之间的区别以及试图衡量的准确性。

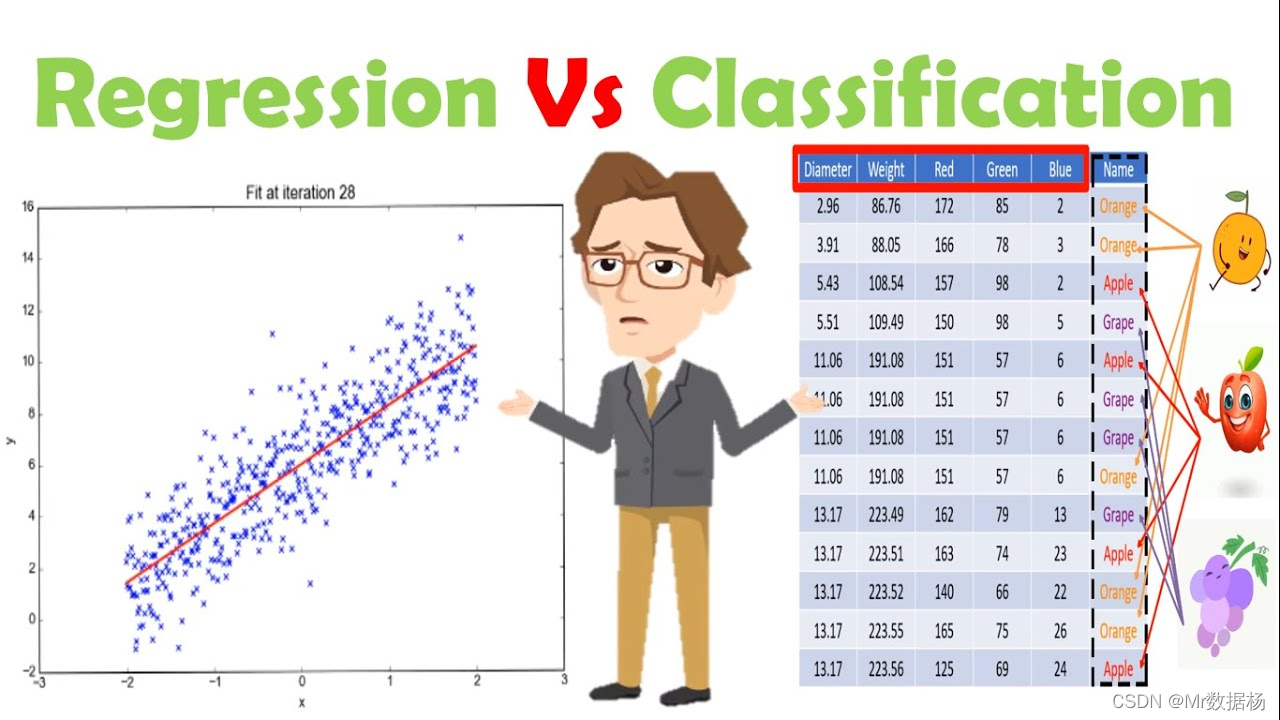
函数近似

预测建模 是使用历史数据开发模型以对我们没有答案的新数据进行预测的问题。

预测建模可以描述为从输入变量 (X) 到输出变量 (y) 逼近映射函数 (f) 的数学问题。这称为函数逼近问题。建模算法的工作是在给定可用时间和资源的情况下找到最佳映射函数。

一般来说，我们可以将所有的函数逼近任务分为分类任务和回归任务。

分类预测建模

分类预测建模是从输入变量 (X) 到离散输出变量 (y) 逼近映射函数 (f) 的任务。

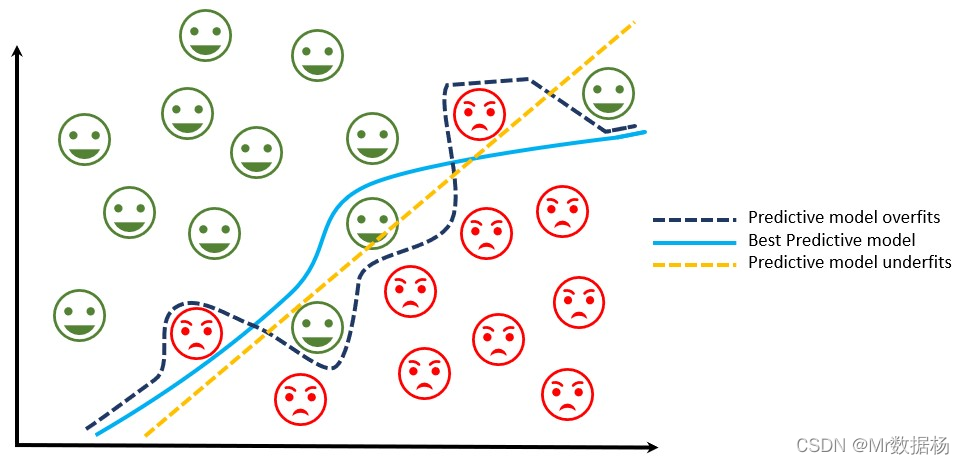
输出变量通常称为标签或类别。映射函数预测给定观察的类别或类别。

例如，一封文本电子邮件可以归类为属于以下两类之一：“垃圾邮件”和“非垃圾邮件”。

• 分类问题要求将示例分类为两个或多个类别之一。
• 分类可以具有实值或离散输入变量。
• 具有两个类别的问题通常称为二分类或二元分类问题。
• 具有两个以上类的问题通常称为多类分类问题。
• 一个例子被分配多个类的问题称为多标签分类问题。

分类模型通常将连续值预测为给定示例属于每个输出类的概率。概率可以解释为属于每个类的给定示例的可能性或置信度。通过选择具有最高概率的类标签，可以将预测概率转换为类值。

例如，特定的文本电子邮件可能被指定为 0.1 为“垃圾邮件”的概率和 0.9 为“非垃圾邮件”的概率。我们可以通过选择“非垃圾邮件”标签将这些概率转换为类别标签，因为它具有最高的预测可能性。

有很多方法可以估计分类预测模型的技能，但最常见的方法可能是计算分类准确度。

分类准确率是所有预测中正确分类的示例的百分比。

例如，如果一个分类预测模型做出了 5 个预测，其中 3 个是正确的，2 个是错误的，那么仅基于这些预测的模型的分类精度将是：

accuracy = correct predictions / total predictions * 100
accuracy = 3 / 5 * 100
accuracy = 60%

能够学习分类预测模型的算法称为分类算法。

回归预测建模

回归预测建模是将映射函数 (f) 从输入变量 (X) 逼近到连续输出变量 (y) 的任务。

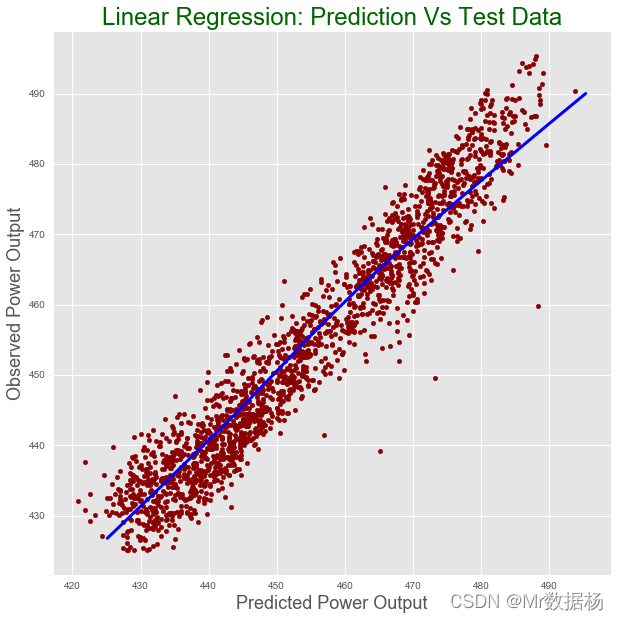
连续输出变量是实数值，例如整数或浮点值。这些通常是数量，例如数量和大小。

例如，可以预测一所房子以特定的美元价值出售，可能在 200,000。

• 回归问题需要对数量进行预测。
• 回归可以具有实值或离散输入变量。
• 具有多个输入变量的问题通常称为多元回归问题。
• 输入变量按时间排序的回归问题称为时间序列预测问题。

因为回归预测模型预测一个数量，所以模型的技能必须在这些预测中报告为错误。

有很多方法可以估计回归预测模型的技能，但最常见的方法可能是计算均方根误差，缩写为 RMSE。

例如，如果回归预测模型进行了 2 个预测，其中一个是 1.5，其中预期值为 1.0，另一个是 3.3，预期值为 3.0，则 RMSE 将为：

RMSE = sqrt(average(error^2))
RMSE = sqrt(((1.0 - 1.5)^2 + (3.0 - 3.3)^2) / 2)
RMSE = sqrt((0.25 + 0.09) / 2)
RMSE = sqrt(0.17)
RMSE = 0.412

RMSE 的一个好处是误差分数的单位与预测值的单位相同。

能够学习回归预测模型的算法称为回归算法。

一些算法的名称中带有“回归”一词，例如线性回归和逻辑回归，这可能会使事情变得混乱，因为线性回归是一种回归算法，而逻辑回归是一种分类算法。

分类与回归

分类预测建模问题不同于回归预测建模问题。

分类是预测离散类标签的任务。
回归是预测连续数量的任务。
分类和回归算法之间存在一些重叠；例如：

• 分类算法可以预测一个连续值，但连续值的形式是类别标签的概率。
• 回归算法可以预测一个离散值，但离散值以整数形式存在。

一些算法经过小的修改即可用于分类和回归，例如决策树和人工神经网络。某些算法不能或不能轻松用于这两种问题类型，例如用于回归预测建模的线性回归和用于分类预测建模的逻辑回归。

重要的是，我们评估分类和回归预测的方式各不相同并且不会重叠，例如：

• 分类预测可以使用准确性进行评估，而回归预测则不能。
• 回归预测可以使用均方根误差进行评估，而分类预测则不能。

在分类和回归问题之间转换

在某些情况下，可以将回归问题转换为分类问题。例如，要预测的数量可以转换为离散的桶。

例如，金额在以下连续范围内 100 可以转换为 2 个类别：

class_type_1： 0-49
class_type_2： 50-100

这通常称为离散化，结果输出变量是一个分类，其中标签具有有序关系（称为序数）。

在某些情况下，分类问题可以转换为回归问题。例如，可以将标签转换为连续范围。

一些算法已经通过预测每个类别的概率来做到这一点，而这些概率又可以缩放到特定范围：

quantity = min + probability * range

或者，类值可以排序并映射到连续范围：

class_type_1： 0-49
class_type_2： 50-100

如果分类问题中的类标签没有自然的序数关系，从分类到回归的转换可能会导致令人惊讶或糟糕的性能，因为模型可能会学习到从输入到连续输出范围的错误或不存在的映射。