目录
1 量纲与无量纲
1.1 量纲
1.2 无量纲
2 标准化
3 归一化
归一化的好处
4 正则化
5 总结
1 量纲与无量纲
1.1 量纲
物理量的大小与单位有关。就比如1块钱和1分钱,就是两个不同的量纲,因为度量的单位不同了。
1.2 无量纲
物理量大小与单位无关。例如角度、增益、两个长度之比等
2 标准化
梯度下降是受益于特征缩放的算法之一。有一种特征缩放的方法叫标准化,标准化使得数据呈现正态分布,能够帮助梯度下降中学习进度收敛的更快。
标准化移动特征的均值(期望),使得特征均值(期望)为0,每个特征的标准差为1。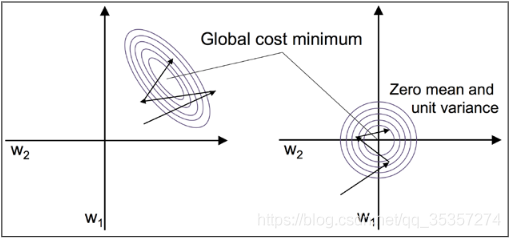
为何标准化能够帮助梯度下降学习是因为优化器需要经历一些步骤才能找到好的或最优的方案(全局最小代价),如图所示,这表示了一个二分类问题中,关于两个权重的代价曲线函数。
而我们再来看看图,图的正中心代表着全局最优的代价(代价最小),而左边的图w2方向比较窄,w1方向又比较宽,那么在梯度下降的过程中,在w2方向梯度会很小,所以会一直寻找最优的点,那么带来了迭代次数变多的后果,降低了效率。
而当对其标准化后,变为了右图这种0均值,1标准差的情况,那么在梯度下降的过程中,不会因为某个方向梯度过小而带来更多的迭代。
3 归一化
归一化(normalization)和标准化(standardization)区别不是很大,都是特征缩放(feature scale)的方式。
有的资料中说的,归一化是把数据压缩到[0,1],把量纲转为无量纲的过程,方便计算、比较等。
我们有两种普通的方法来将不同的特征带到同样的范围:归一化(normalization)和标准化(standardization)。这两个术语在不同领域的使用比较松散,通常需要靠上下文来判断它们的含义。普遍情况下,归一化指的是将特征缩放到[0,1]这个区间,这是一个“min-max scaling”的特殊栗子。
而对于不同特征列向量来说,常用的归一化方法:min-max scaling公式如下: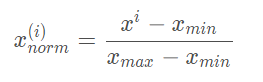

归一化还有一点,就是说归到[ 0 , 1 ]区间后,并不会改变原本的数值大小排序关系。就比如上面的栗子,[ 1 , 5 , 3 ]的大小关系为( 1 , 3 , 2 ),归一化为[ 0 , 1 , 0.5 ] 后的大小关系依旧为( 1 , 3 , 2 ),并没有发生变化。
归一化的好处
- 提升模型的收敛速度
- 提升模型的精度
那么关于归一化、标准化的本质区别就是说:归一化是将特征缩放到[ 0 , 1 ] 区间,标准化是把特征缩放到均值为0,标准差为1。
4 正则化
正则化(regularization)是与标准化还有归一化完全不同的东西。正则化相当于是个惩罚项,用于惩罚那些训练的太好的特征/参数,防止模型过拟合,提高模型的泛化能力。
正则化就是用来处理collinearity的,这个collinearity指的是与特征高度相关,清理掉数据的噪声,最终阻止过拟合。而正则化实际上就是引入一个额外的信息(偏置)来惩罚极端的参数(权重)值。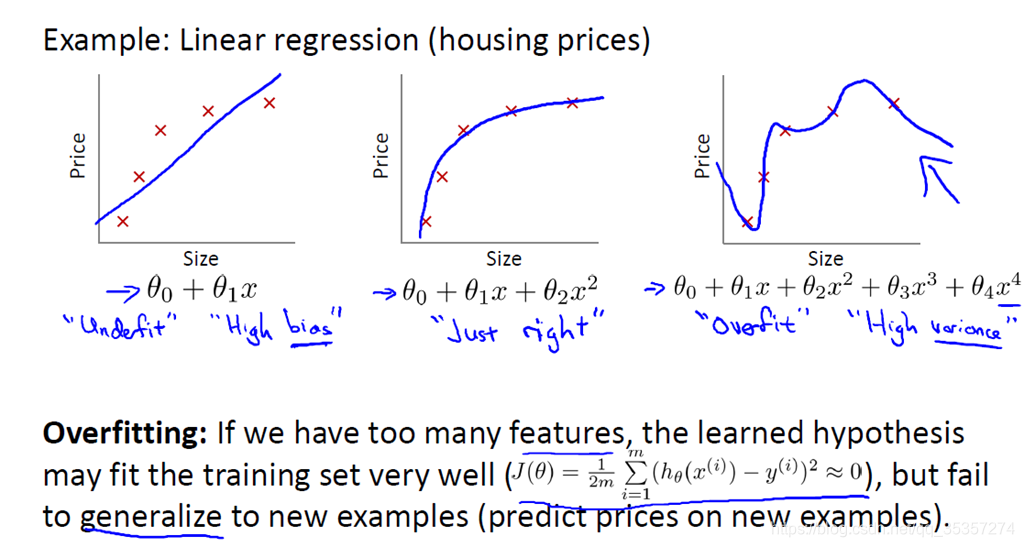
我们看到图三这个曲线非线性拟合的太完美了,那么就造成了过拟合,造成的原因是因为特征过多,训练的太好了,而这个特征过多,我个人认为就对应了上面英文中的collinearity (high correlation among features)。
我们再来分析图二和图三的公式,多了的特征是x^3 和x^4,为何多了这两个就造成了图三这样的车祸现场(因为拟合的太好了,导致泛化性能很差,当有新的特征来的时候就哦豁了)?大家不妨回忆下泰勒级数,就是用多项式逼近任意一个曲线,这里也是同样的道理。那么我们要怎样解决过拟合?我们有以下两种方法:
1.减少特征个数(特征约减):
手工保留部分特征(你觉得你能做到么?反正我觉得我做不到)
模型选择算法(PCA,SVD,卡方分布)
2.正则化:保留所有特征,惩罚系数θ,使之接近于0,系数小,贡献就小。所以也就对应了书本上的惩罚极端参数值。
正则化通常采用L2正则化,公式如下: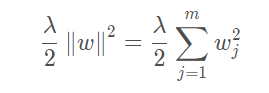
其中λ 称作正则化项。这里1/2是方便求导。
关于为何通常采用第二范数而非第一范数,我个人认为有如下两个理由:
- 计算机中计算平方比计算绝对值简单;
- 第二范数是光滑且可求导的,但是第一范数至少在0这个点是不可导的。
5 总结
量纲与无量纲的区别就是:物理量是否与单位有关。
标准化与归一化没有显著的区别,具体是谁要依据上下文确定。归一化是把特征缩放到[ 0 , 1 ],标准化是把特征缩放到均值为0,标准差为1。
正则化是与标准化和归一化完全不同的东西,是用于惩罚训练的太好的参数,防止模型过拟合,提高模型的泛化能力。
原文:机器学习学习笔记(3)——量纲与无量纲,标准化、归一化、正则化_LiQZ的博客-CSDN博客_量纲归一化

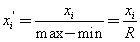

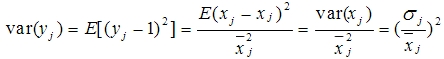



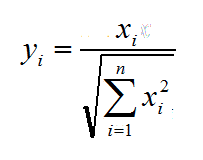
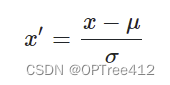
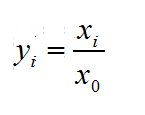

![LaTex排版技巧:[15]公式太长如何换行](https://imgsa.baidu.com/exp/w=500/sign=185604bfd2160924dc25a21be406359b/b8014a90f603738d07dc6fcbb11bb051f919ec41.jpg)