摘要:本文用实例说明了多指标综合评价中,用“倒数逆变换法”进行指标正向化时会完全改变原指标的分布规律,影响综合评价结果的准确性;对三种常用无量纲化方法——极差变换法、标准化法和均值化法的选择使用问题,用实例进行了比较分析。
关键词:综合评价,正向化,无量纲化,标准化法,均值化法
在多指标综合评价中,有些是指标值越大评价越好的指标,称为正向指标(也称效益型指标或望大型指标);有些是指标值越小评价越好的指标,称为逆向指标(也称成本型指标或望小型指标),还有些是指标值越接近某个值越好的指标,称为适度指标。在综合评价时,首先必须将指标同趋势化,一般是将逆向指标和适度指标转化为正向指标,所以也称为指标的正向化。不同评价指标往往具有不同的量纲和量纲单位,直接将它们进行综合是不合适的,也没有实际意义。所以必须将指标值转化为无量纲的相对数。这种去掉指标量纲的过程,称为指标的无量纲化(也称同度量化),它是指标综合的前提。在多指标评价实践中,常将指标无量纲化以后的数值作为指标评价值,此时,无量纲化过程就是指标实际值转化为指标评价值(即效用函数值)的过程,无量纲化方法也就是指如何实现这种转化。从数学角度讲就是要确定指标评价值依赖于指标实际值的一种函数关系式,即效用函数fj。因此,指标的无量纲化是综合评价的一项重要内容,对综合评价结果有重要影响。
指标的正向化和无量纲化都有多种方法,应用时,应根据实际情况选择合适的方法,否则将会使综合评价的准确性受到影响。本章就如何选择正向化和无量纲化方法作些讨论。
(一)关于指标正向化方法
对于指标的正向化,在实际应用中许多学者常使用将指标取倒数的方法(苏为华教授称其为“倒数逆变换法”),写成公式为:
yij=C/xij (1)
其中C为正常数,通常取C=1。很明显,用(1)式作为指标的正向化公式时,当原指标值xij较大时,其值的变动引起变换后指标值的变动较慢;而当原指标值较小时,其值的变动会引起变换后指标值的较快变动。特别是当原指标值接近0时,变换后指标值的变动会非常快,使得指标评价值的确定,也即指标的无量纲化变得困难。
比如徐国祥等将指标资产负债率、流动比率、速动比率作为适度指标,对它们的正向化方法为
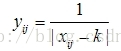
(2)
适度值k取各单位该指标值的平均值。这种取倒数的方法使得:一些接近k的指标值之间的差距扩大,而远离k的指标值之间的差距缩小,因而不能真实反映原指标的分布情况。笔者选取2001年全国各地区全部国有及规模以上非国有工业企业主要经济效益指标中的资产负债率为例(为节省篇幅选前10个省市的值),用(2)式进行正向化变换,10个省市的资产负债率及其正向化值见表1。资产负债率的平均值k=58.59。
表1 10省市资产负债率及其正向化值
| 地区 | 北京 | 天津 | 河北 | 山西 | 内蒙古 | 辽宁 | 吉林 | 黑龙江 | 上海 | 江苏 |
| 资产负债率(%) | 55.29 | 58.28 | 63.25 | 63.79 | 58.44 | 58.69 | 62.63 | 59.02 | 46.46 | 60.03 |
| 正向化值 | 0.30 | 3.25 | 0.21 | 0.19 | 6.76 | 9.80 | 0.25 | 2.31 | 0.08 | 0.69 |
资料来源:中国统计年鉴(2002).中国统计出版社,下同.
由表1可见,天津与内蒙古的资产负债率原值为58.28和58.44,相差极小,而变换后的值分别为3.25和6.76,相差很大;北京和上海的原值分别为55.29和46.46,相差很大,而变换后的值为0.30和0.08,相差很小。但另一方面,从资产负债率对经济效益的影响程度分析,当资产负债率在平均值附近时,其值的变动对经济效益的影响较小;当资产负债率远离平均值时,其值的变动对经济效益的影响较大。可见用这种取倒数的变换方法完全改变了原指标的分布规律,所得综合评价结果肯定是不准确的,因而是不可取的。
笔者认为,应尽可能不使用这种倒数逆变换法,而使用“倒扣逆变换法”,即对逆向指标正向化公式为
对适度指标正向化公式为
这种线性变换不会改变指标值的分布规律。
但是,对周转速度类指标(包括库存商品周转速度、流动资金周转速度等等)通常有正向指标“次数”和逆向指标“天数”两种表现形式,二者存在互逆关系:
周转天数(天/次)=报告期日历长度(天)/报告期周转次数(次)
显然,“次数”的增加能很好地表现实际价值的增加,“次数”是较好的评价指标,所以用倒数逆变换法将逆向指标“天数”变换为正向指标“次数”是较好的正向化方法。
(二)指标无量纲化方法的选择
目前人们已提出的无量纲化方法名称很多,如综合指数法、极差变换法、高中差变换法、低中差变换法、均值化法、标准化法、比重法、功效系数法、指数型功效系数法、对数型功效系数法、正态化变换法等等。苏为华教授将它们归为四类:广义指数法、广义线性功效系数法、非线性函数法、分段函数法[1]。则广义指数法和广义线性功效系数法包含了前8种,都是线性无量纲化方法;后三种属于非线性函数法,也即曲线型无量纲化方法。由于指数或对数变换时,曲线的增减速度、凹凸程度很难把握,所以实践中非线性函数法较少被采用。
实践中应用较多的是属于直线型无量纲化方法的极差变换法、标准化法和均值化法。下面对这三种方法进行比较分析。
设综合评价中共有n个单位,m个指标,各指标分别为x1,x2,…,xm,用xij(i=1,2,…,n;j=1,2,…,m)表示第i个单位的第j个原始指标值,yij表示经过无量纲化处理的第i个单位的第j个指标值。极差变换法即令
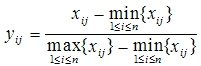
式(3)中的分母仅与原始指标的最大值和最小值有关,而与指标的其它值无关。当xj的最大值与最小值之差很大时,yj值就会过小,相当于降低了第j个指标的权重;相反,当xj的最大值与最小值之差很小时,yj值就会过大,相当于提高了第j个指标的权重。即指标的两个值就对指标的权重产生了很大影响。所以在多指标综合评价中,用极差变换法作为无量纲化的方法是不可取的。
目前最普遍使用的无量纲化方法是标准化法,标准化法即令
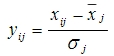
其中和σj分别是指标xj的均值和标准差。经标准化后,指标yj的均值为0,方差为1,消除了量纲和数量级的影响。同时标准化法也消除了各指标变异程度上的差异,因此经标准化后的数据不能准确反映原始数据所包含的信息,导致综合评价的结果不准确。从下例可以看出:
例1、对十个省市的全部国有及规模以上非国有工业企业的经济效益进行综合评价。为直观起见,只选用全员劳动生产率和产品销售率两个指标,指标值见表2。根据国家经贸委等部门颁布的《工业经济效益评价体系》两个指标的权数分别为10和13。
表2 十省市劳动生产率和产品销售率
| 地区 | 北京 | 天津 | 河北 | 山西 | 内蒙古 | 辽宁 | 吉林 | 黑龙江 | 上海 | 江苏 |
| 劳动生产率(元) | 69539 | 58984 | 45576 | 27988 | 37770 | 48170 | 47306 | 68104 | 95393 | 57177 |
| 产品销售率(%) | 98.17 | 98.02 | 98.05 | 97.06 | 97.93 | 97.33 | 96.94 | 97.61 | 98.83 | 97.06 |
由表2易见,各地区的产品销售率非常接近,而全员劳动生产率相差较大。它们的变异系数分别为0.0062和0.3419也说明了这一点。所以若用这两个指标来评价经济效益,则很显然主要的影响因素应是全员劳动生产率。
但是,若用标准化法对两个指标进行无量纲化,将使两个指标的变异程度相同,因为产品销售率的权数大,因而产品销售率对经济效益的影响会比全员劳动生产率大。评价结果见表3
表3 十省市标准化法评价结果对照
| 地区 | 北京 | 天津 | 河北 | 山西 | 内蒙古 | 辽宁 | 吉林 | 黑龙江 | 上海 | 江苏 |
| 评价得分 | 0.76 | 0.38 | 0.10 | -1.23 | -0.19 | -0.51 | -0.90 | 0.20 | 1.96 | -0.56 |
| 评价名次 | 2 | 3 | 5 | 10 | 6 | 7 | 9 | 4 | 1 | 8 |
| 销售率名次 | 2 | 4 | 3 | 8 | 5 | 7 | 10 | 6 | 1 | 8 |
从表3可见评价名次与产品销售率名次相差不大,这显然是不合理的。
所以必须改进原始数据的无量纲化方法,均值化方法就是一种较好的方法。均值化方法即令
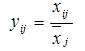
均值化后各指标的均值都为1,其方差为
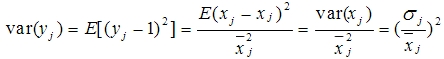
即均值化后各指标的方差是各指标变异系数的平方,它保留了各指标变异程度的信息。
对于例1,若用均值化方法对两个指标进行无量纲化,则因全员劳动生产率的变异系数比产品销售率的变异程度大得多,因而全员劳动生产率是经济效益综合评价的主要影响因素。评价结果见表4
表4 十省市均值化法评价结果对照
| 地区 | 北京 | 天津 | 河北 | 山西 | 内蒙古 | 辽宁 | 吉林 | 黑龙江 | 上海 | 江苏 |
| 评价得分 | 1.11 | 1.03 | 0.92 | 0.78 | 0.86 | 0.94 | 0.93 | 1.10 | 1.32 | 1.01 |
| 评价名次 | 2 | 4 | 8 | 10 | 9 | 6 | 7 | 3 | 1 | 5 |
| 劳动生产率名次 | 2 | 4 | 8 | 10 | 9 | 6 | 7 | 3 | 1 | 5 |
由表4可知,评价名次与全员劳动生产率的名次完全一致,这与实际情况是相符的。即用均值化法比用标准化法合理。
那么,是否我们就应该用均值化方法作为指标的无量纲化方法呢?这也要具体问题具体分析。在实际问题中,情况是复杂的,有时需要保留指标的变异信息,有时需要消除指标的变异信息。用下面的例子即可说明。
例2、某校在对教师进行考核时,其考核方法为根据教师所任教班级的学生打分和由学校领导、教师代表组成的考核小组打分各占50%的比例进行综合。现选择其中10位教师的分数如表5:
表5 10位教师的原始考核分
| 教师编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 学生打分 | 81.3 | 94.7 | 84.7 | 95.2 | 93.2 | 98.5 | 92 | 86.5 | 89.9 | 84.6 |
| 考核小组打分 | 90.3 | 93.5 | 91.1 | 94 | 94.5 | 93.6 | 91.5 | 90.4 | 93 | 91.7 |
易见学生打分的变异程度远大于考核小组打分的变异程度,若为了保留指标的变异信息,采用均值化方法作无量纲化处理,可得各教师的综合考核分及名次如表6(因两种打分的量纲一致,也可以不作无量纲化处理,所得结果相同)
表6 10位教师的均值化方法考核结果
| 教师编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 综合考核分 | 0.940 | 1.032 | 0.963 | 1.037 | 1.029 | 1.054 | 1.006 | 0.970 | 1.003 | 0.966 |
| 综合考核名次 | 10 | 3 | 9 | 2 | 4 | 1 | 5 | 7 | 6 | 8 |
| 学生打分名次 | 10 | 3 | 8 | 2 | 4 | 1 | 5 | 7 | 6 | 9 |
除3号和10号教师外,考核名次与学生打分的名次均相同,即考核小组的打分几乎不起作用,这显然极不合理。
一般来说,类似例1这样的由主观打分的综合评价问题,不应保留指标的变异信息,而应消除指标的变异信息。用标准化方法即能消除指标的变异信息,使两种打分起同等作用。用此法可得各教师的综合考核分及名次如表7。显然,表7的结果会更加合理。
表7 10位教师的标准化方法考核结果
| 教师编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 综合考核分 | -1.45 | 0.79 | -0.89 | 0.99 | 0.98 | 1.16 | -0.11 | -0.96 | 0.19 | -0.70 |
| 名次 | 10 | 4 | 8 | 2 | 3 | 1 | 6 | 9 | 5 | 7 |
根据以上分析,当综合评价的指标值都是客观数值时,一般来说应该用均值化方法对指标进行无量纲化;而当综合评价的指标值是主观分数时,则用标准化方法更好。
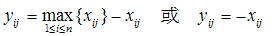
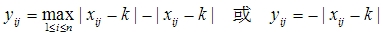



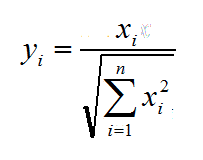
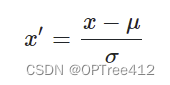
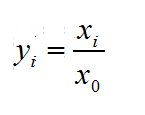

![LaTex排版技巧:[15]公式太长如何换行](https://imgsa.baidu.com/exp/w=500/sign=185604bfd2160924dc25a21be406359b/b8014a90f603738d07dc6fcbb11bb051f919ec41.jpg)