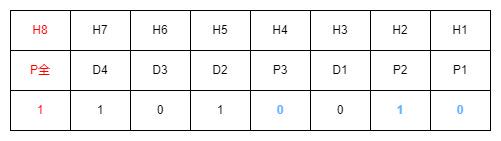
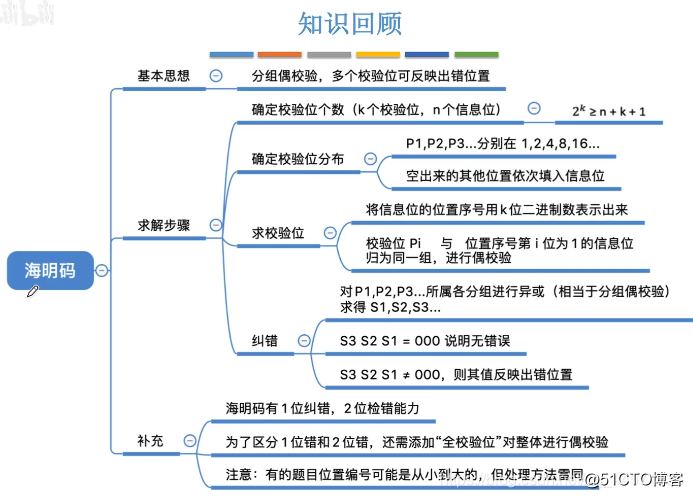
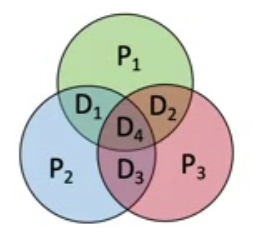
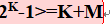我们常见的是纯整数十进制转二进制，而对小数部分的转换不常提及。以下帮助大家梳理
$$\begin{gathered} (xxx.yyy{)}_{10} \\ xxx为整数部分，yyy为小数部分 \end{gathered}$$
核心思想：将整数和小数部分分开计算，最后整合。

1. 对于整数：除二逆向取余
2. 对于小数部分:乘二正向(向下)取整

（一）整数部分
以34举例

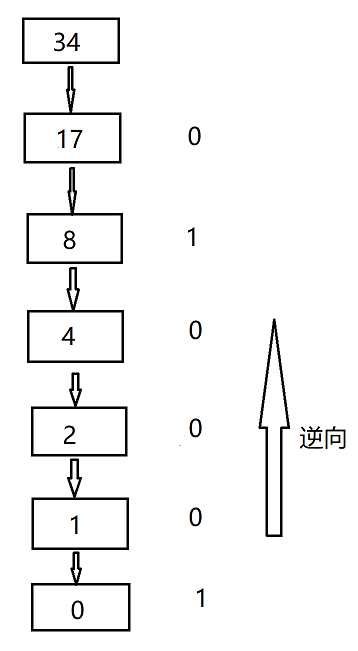
图中每个小箭头代表一次除2
34=17x2+0
17=8x2+1
…以此类推
最后逆向读出。故$(34{)}_{10}$=$(100010{)}_2$
（二）小数部分
以0.625举例

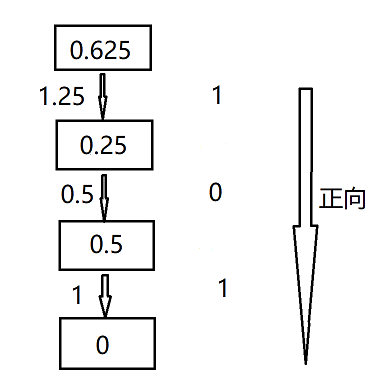
图中每个小箭头代表两个操作:
A$\to$B

1. Ax2
2. B= A-$\lfloor A\rfloor$

0.25=0.625*2=1.25-$\lfloor 1.25\rfloor$ =0.25 ($\lfloor 1.25\rfloor$=1)

0.5=0.25*2=0.5-$\lfloor 0.5\rfloor$=0.5($\lfloor 0.5\rfloor$=0)

最后正向读出。故$(0.625{)}_{10}=(.101{)}_2$

若嫌式子过于复杂，可以这么记忆:
小数部分乘2，若>1，则减去1，在旁边记录下1；
若小于1，则无需减去1，在旁边记录下0；
使其一直为0.xx的形式，如此往复

特别的：小数部分转二进制可能会出现乘不尽，一直不能化为0。此时根据题目要求的精度来决定要多少位二进制即可。

整合
那么34.625的二进制表述就是将其拼接起来
$(34.625{)}_{10}=(100010.101)2$