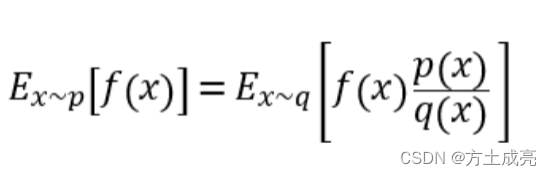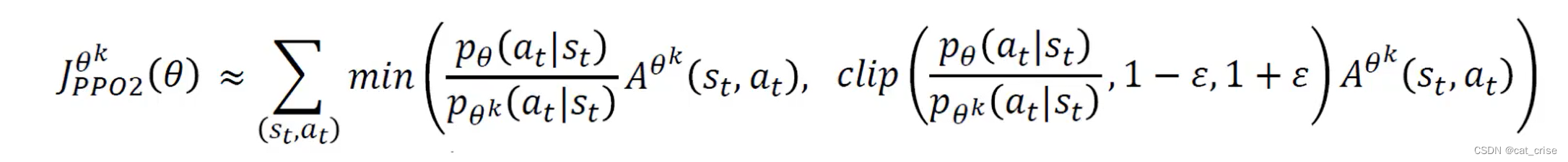回顾
传统的策略梯度算法以下式作为策略网络的损失:
g ^ = E ^ t [ ∇ θ log π θ ( a t ∣ s t ) A ^ t ] \hat{g}=\hat{\mathbb{E}}_{t}\left[\nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{A}_{t}\right] g^=E^t[∇θlogπθ(at∣st)A^t]
具体在代码实现中就是计算 log π θ ( a t ∣ s t ) A ^ t \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{A}_{t} logπθ(at∣st)A^t(蒙特卡洛近似)后反向传播更新策略网络。
容易出现: log π θ ( a t ∣ s t ) A ^ t \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{A}_{t} logπθ(at∣st)A^t是一个绝对值特别大的数,这将导致 π θ ( a t ∣ s t ) \pi _\theta ( a _ { t } | s _ { t } ) πθ(at∣st)与 π θ n e w ( a t ∣ s t ) \pi _{\theta_{new}} ( a _ { t } | s _ { t } ) πθnew(at∣st)差别较大,这不利于收敛:

PPO使用clip解决这个问题
首先PPO在clip前的策略网络损失值如下:
L C P I ( θ ) = E ^ t [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t ] = E ^ t [ r t ( θ ) A ^ t ] L^{C P I}(\theta)=\hat{\mathbb{E}}_{t}\left[\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\mathrm{old}}}\left(a_{t} \mid s_{t}\right)} \hat{A}_{t}\right]=\hat{\mathbb{E}}_{t}\left[r_{t}(\theta) \hat{A}_{t}\right] LCPI(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t]=E^t[rt(θ)A^t]
这个式子其实和传统策略梯度算法的 log π θ ( a t ∣ s t ) A ^ t \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{A}_{t} logπθ(at∣st)A^t大同小异,紧接着对上式做如下操作:
L C L I P ( θ ) = E ^ t [ min ( r t ( θ ) A ^ t , clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t ) ] L^{C L I P}(\theta)=\hat{\mathbb{E}}_{t}\left[\min \left(r_{t}(\theta) \hat{A}_{t}, \operatorname{clip}\left(r_{t}(\theta), 1-\epsilon, 1+\epsilon\right) \hat{A}_{t}\right)\right] LCLIP(θ)=E^t[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t)]
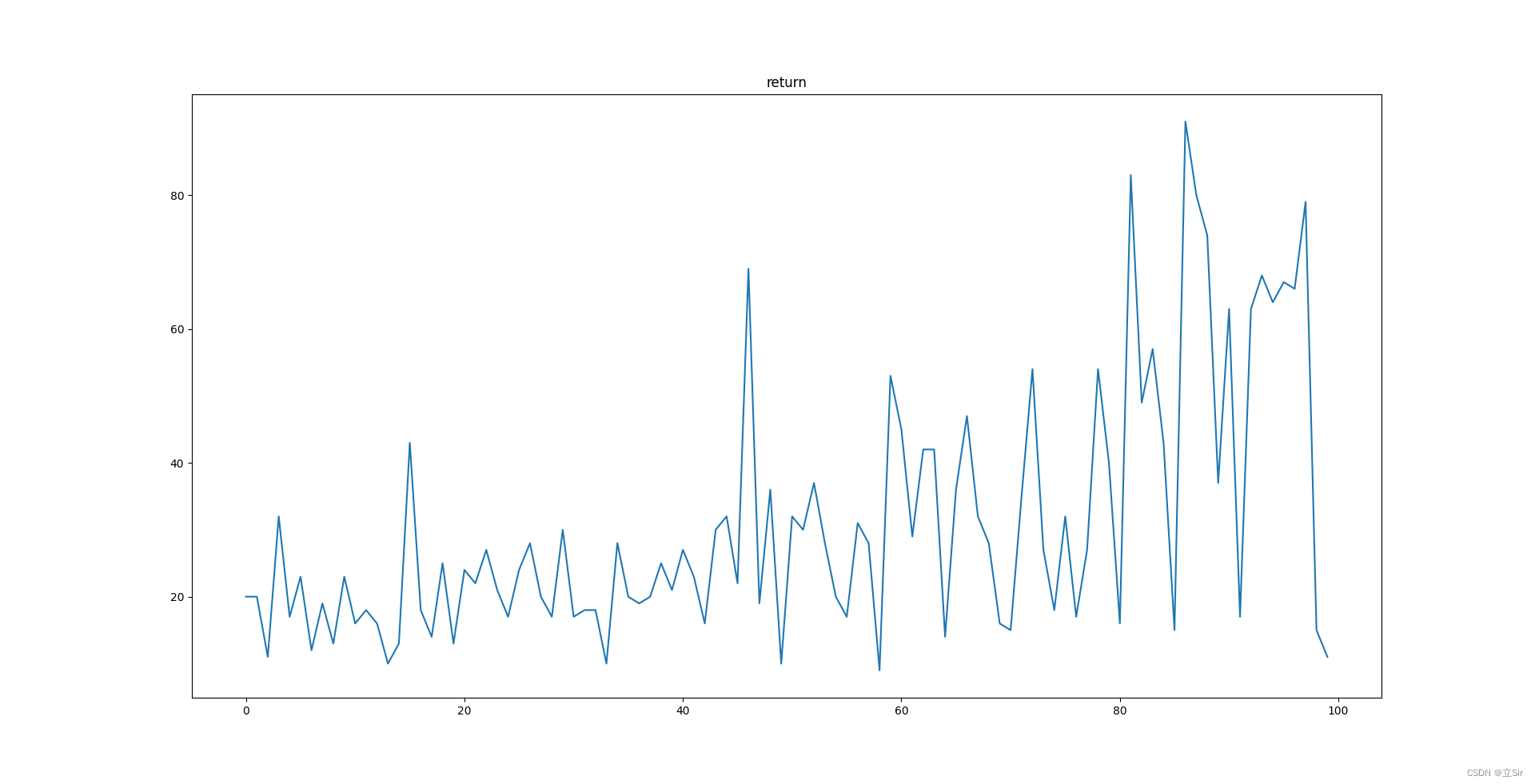
我们分析 L C L I P ( θ ) L^{C L I P}(\theta) LCLIP(θ)和 r t ( θ ) r_t(\theta) rt(θ)的关系,可以绘制出如下两张图:

首先我们需要明确优势函数(advantage function)的定义及含义:
A π ( s t , a t ) = Q π ( s t , a t ) − V π ( s t ) A ^ { \pi } ( s _ { t} ,a_t ) = Q ^ { \pi } ( s _ { t },a_t ) - V ^ { \pi } ( s _ { t } ) Aπ(st,at)=Qπ(st,at)−Vπ(st)
又因为 V π ( s t ) V ^ { \pi } ( s _ { t } ) Vπ(st)是状态 s t s _ { t } st下对 Q π ( s t , a t ) Q ^ { \pi } ( s _ { t },a_t ) Qπ(st,at)的加权平均,因此 V π ( s t ) V ^ { \pi } ( s _ { t } ) Vπ(st)反映的是在当前策略下做出动作的平均累计折扣回报的期望,可以理解为平均水平,因此 A π ( s t , a t ) A ^ { \pi } ( s _ { t} ,a_t ) Aπ(st,at)反映的是做动作 a t a_t at带来的优势,因此 A π ( s t , a t ) > 0 A ^ { \pi } ( s _ { t} ,a_t )>0 Aπ(st,at)>0的情况下策略梯度算法将向着提高 π ( a t ∣ s t ) \pi(a_t|s_t) π(at∣st)的方向前进,当 A π ( s t , a t ) < 0 A ^ { \pi } ( s _ { t} ,a_t )<0 Aπ(st,at)<0时策略梯度算法将向着减小 π ( a t ∣ s t ) \pi(a_t|s_t) π(at∣st)的方向前进(这里也可以这么理解:最大化loss,当A>0,自然是要增大r,就是增大 π \pi π,当A<0,要最大化loss就要最小化r,因此减小 π \pi π)。
分析第一张图:只要当前策略在动作 a t a_t at下的 π \pi π相对于上次更新前 π o l d \pi_{old} πold之比过大,即超过 1 + ϵ 1+\epsilon 1+ϵ,根据图中函数关系可知loss关于r的梯度为0,这次反向传播不会对权重产生影响,如果小于 1 + ϵ 1+\epsilon 1+ϵ正常更新。
第二张图:A<0,说明这个动作不够好,r是往小的方向更新,但是如果之前更新的比例r已经小于了 1 − ϵ 1-\epsilon 1−ϵ,说明更新幅度之前已经比较大了,不建议再往这个方向更新,根据图中函数关系此时loss关于r的梯度为0,不会对权重产生影响。
综上所述: PPO在该动作是好动作的情况下限制它往好的方向(概率增大)过度更新,在该动作是差动作的情况下限制它往差的方向(概率减小)过度更新,从而达到限制更新幅度的想法。