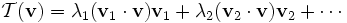(下面的回答只涉及实数范围)。
关于特征值、特征向量可以讲的确实很多,我这里希望可以给大家建立一个直观的印象。
先给一个简短的回答,如果把矩阵看作是运动,对于运动而言,最重要的当然就是运动的速度和方向,那么(我后面会说明一下限制条件):
- 特征值就是运动的速度
- 特征向量就是运动的方向
既然运动最重要的两方面都被描述了,特征值、特征向量自然可以称为运动(即矩阵)的特征。
注意,由于矩阵是数学概念,非常抽象,所以上面所谓的运动、运动的速度、运动的方向都是广义的,在现实不同的应用中有不同的指代。
下面是详细的回答,我会先从几何上简单讲解下特征值、特征向量的定义指的是什么,然后再来解释为什么特征值、特征向量会是运动的速度和方向。
1 几何意义
说明下,因为线性变换总是在各种基之间变来变去,所以我下面画图都会把作图所用的基和原点给画出来。
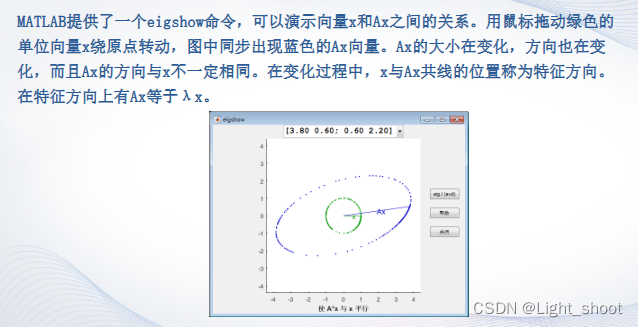
在 下面有个
:
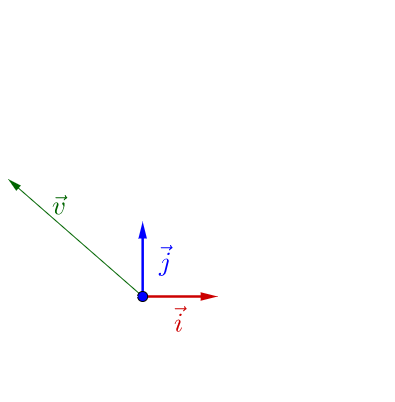
随便左乘一个矩阵,图像看上去没有什么特殊的:
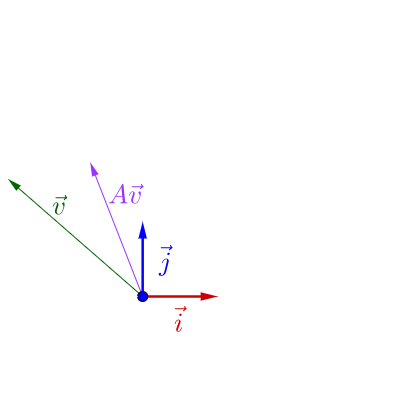
我调整下 的方向,图像看上去有点特殊了:
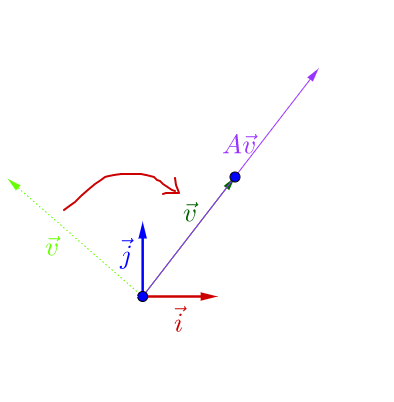
可以观察到,调整后的 和
在同一根直线上,只是
的长度相对
的长度变长了。
此时,我们就称 是
的特征向量,而
的长度是
的长度的
倍,
就是特征值。
从而,特征值与特征向量的定义式就是这样的:
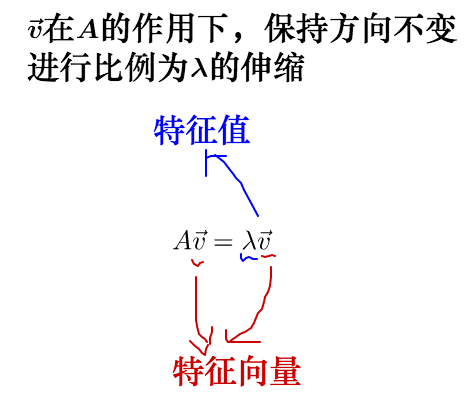
其实之前的 不止一个特征向量,还有一个特征向量:
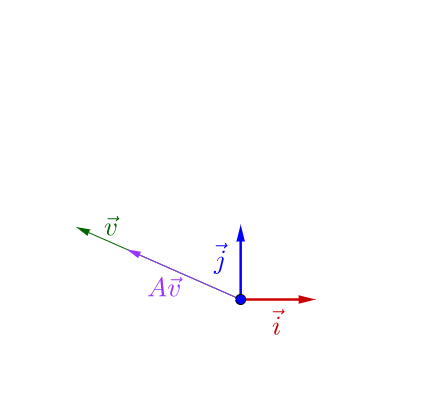
容易从 相对于
是变长了还是缩短看出,这两个特征向量对应的特征
值,一个大于1,一个小于1。
从特征向量和特征值的定义式还可以看出,特征向量所在直线上的向量都是特征向量:
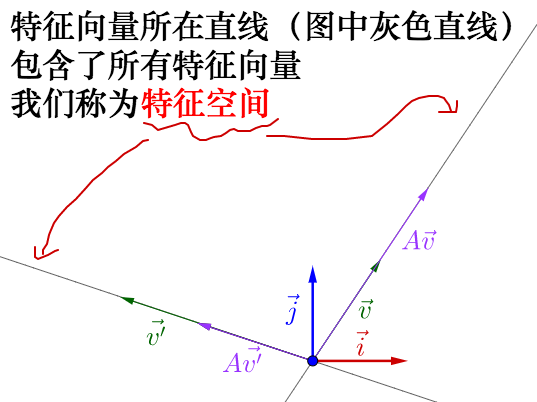
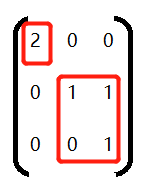
你可以自己动手试试,可以改变 的位置,以及矩阵
的值(特征空间会随着矩阵改变而改变):
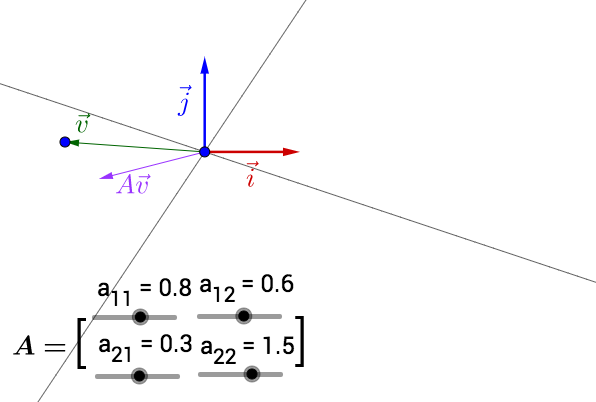
此处有互动内容, 点击此处前往操作。
其中有些值构成的矩阵没有画出特征空间,可能是因为它的特征值、特征向量是复数,也可能是不存在。
下面就要说下,特征值、特征向量与运动的关系
2 运动的速度与方向
2.1 从调色谈起
我有一管不知道颜色的颜料,而且这管颜料有点特殊,我不能直接挤出来看颜色,只能通过调色来观察:

为了分辨出它是什么颜色(记得它只能通过调色来辨别):
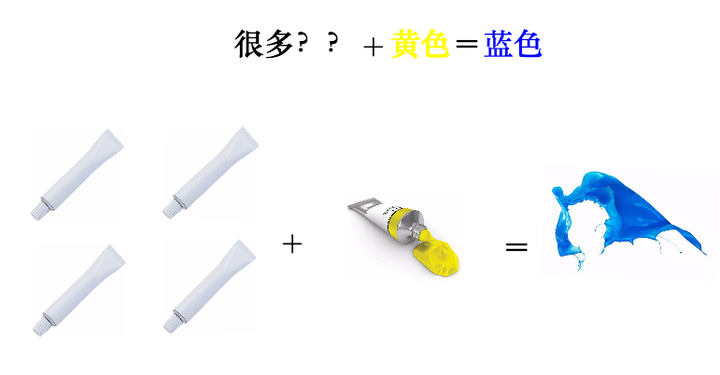
因为反复混合之后,这管颜料的特征就凸显了出来,所以我们判断,这管颜料应该是蓝色。
说这个干什么?矩阵也有类似的情况。
2.2 矩阵的混合
一般来说,矩阵我们可以看作某种运动,而二维向量可以看作平面上的一个点(或者说一个箭头)。对于点我们是可以观察的,但是运动我们是不能直接观察的。
就好像,跑步这个动作,我们不附加到具体的某个事物上是观察不到的,我们只能观察到:人跑步、猪跑步、老虎跑步、......,然后从中总结出跑步的特点。
就好像之前举的不能直接观察的颜料一样,要观察矩阵所代表的运动,需要把它附加到向量上才观察的出来:
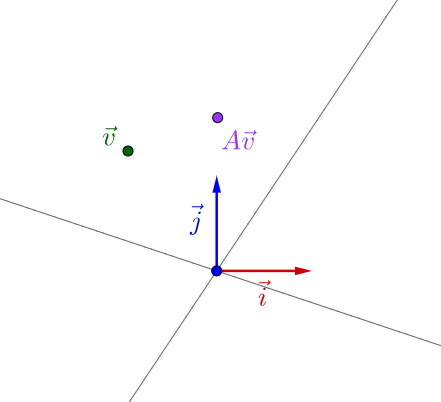
似乎还看不出什么。但是如果我反复运用矩阵乘法的话:
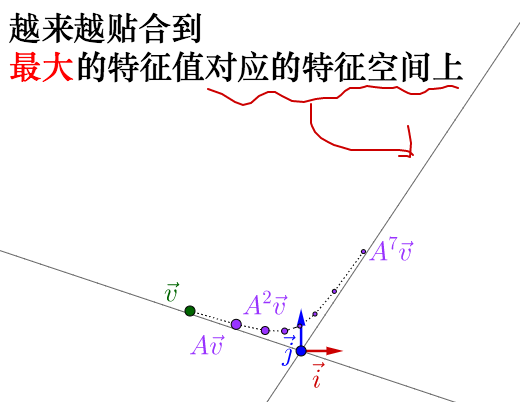
就像之前颜料混合一样,反复运用矩阵乘法,矩阵所代表的运动的最明显的特征,即速度最大的方向,就由最大特征值对应的特征向量展现了出来。
至于别的特征值对应的是什么速度,我后面会解释,这里先跳过。
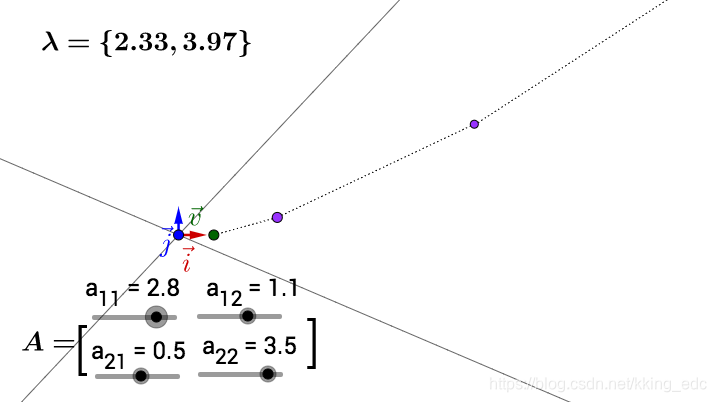
可以自己动手试试,我把 值也标注出来了,可以关注下最大
值对于运动的影响:
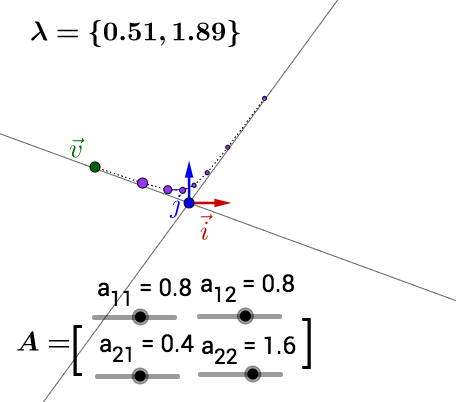
此处有互动内容, 点击此处前往操作。
顺便说下,对于复数的特征值、特征向量,在上面就没有画出特征空间,但可以观察到反复运用矩阵乘法的结果是围绕着原点在旋转。关于复数特征值和特征向量这里就不展开来说了。
2.3 烧一壶斐波那契的水
上面说的运动太抽象了,我来举一个具体点的例子:烧水。
比如说我想烧一壶水,水的温度按照斐波那契数列升高,即下一秒的温度 与当前温度
以及上一秒的温度
的关系为:
要继续计算下去,我只需要 以及
就可以继续算下去。因此我可以写成下面的式子:
因此烧水这个运动我们可以抽象为矩阵 ,反复进行这个运动就可以烧开这壶水,根据斐波那契数列,让我们从
点开始(感兴趣的话,可以通过之前的互动调整下参数,可以得到下面的结果):

就可以看出,这壶水的温度会沿着的特征值最大的特征向量方向飞快增长,我估计要不了多久,在理想的情况下,温度就会突破百万度、千万度、亿万度,然后地球说不定就爆炸了。我们就说这个矩阵不稳定。
所以说,不要烧斐波那契的水。
实际上历史也是这样,欧拉在研究刚体的运动时发现,有一个方向最为重要,后来拉格朗日发现,哦,原来就是特征向量的方向。
我们知道特征值、特征向量有什么特点之后,下一步就想知道,为什么会这样?
3 特征值分解
下面讲解要用到矩阵乘法和相似矩阵的知识,我就不啰嗦了,可以参看我的回答: 行列式的本质是什么? 以及 相似矩阵是什么?
我们知道,对于矩阵可以对角化的话,可以通过相似矩阵进行下面这样的特征值分解:
其中为对角阵,
的列向量是单位化的特征向量。
说的有点抽象,我们拿个具体的例子来讲:
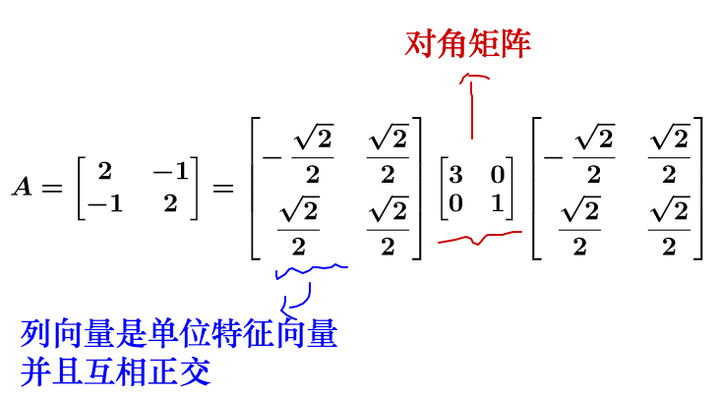
对于方阵而言,矩阵不会进行维度的升降,所以矩阵代表的运动实际上只有两种:
- 旋转
- 拉伸
最后的运动结果就是这两种的合成。
我们再回头看下刚才的特征值分解,实际上把运动给分解开了:

我们来看看在几何上的表现是什么,因此相似矩阵的讲解涉及到基的变换,所以大家注意观察基:
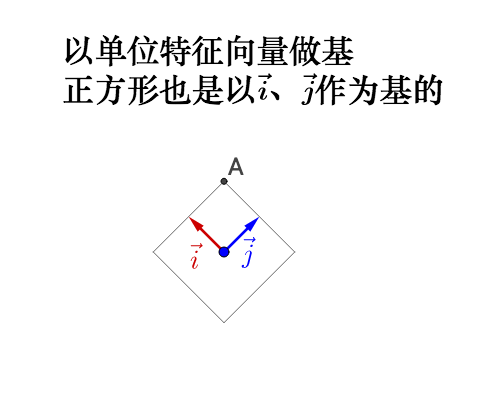
左乘 :
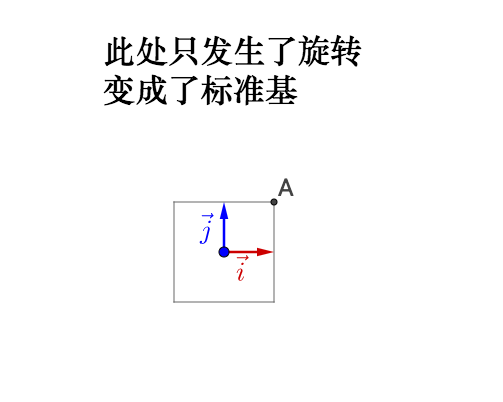
如果旋转前的基不正交,旋转之后变为了标准基,那么实际会产生伸缩,所以之前说的正交很重要。
继续左乘对角矩阵 :
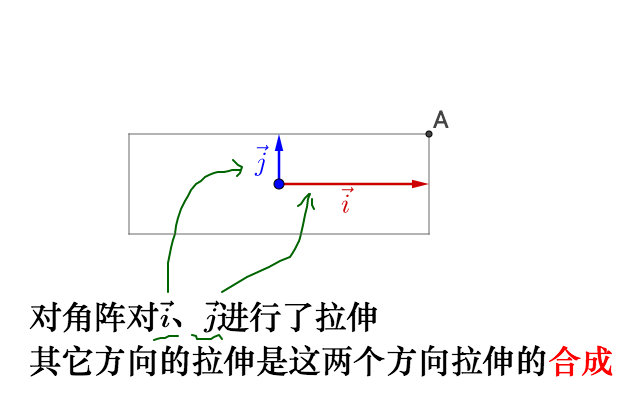
相当于,之前的旋转是指明了拉伸的方向,所以我们理解了:
- 特征值就是拉伸的大小
- 特征向量指明了拉伸的方向
回到我们之前说的运动上去,特征值就是运动的速度,特征向量就是运动的方向,而其余方向的运动就由特征向量方向的运动合成。所以最大的特征值对应的特征向量指明了运动速度的最大方向。
但是,重申一下,上面的推论有一个重要的条件,特征向量正交,这样变换后才能保证变换最大的方向在基方向。如果特征向量不正交就有可能不是变化最大的方向,比如:
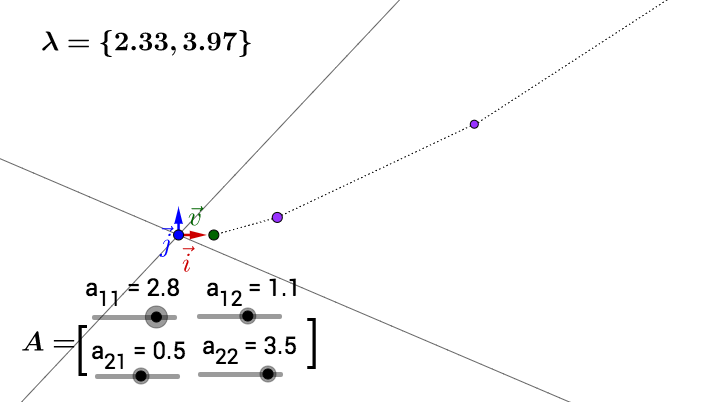
所以我们在实际应用中,都要去找正交基。但是特征向量很可能不是正交的,那么我们就需要奇异值分解了,这里就不展开了。
大家可以再回头去操作一下之前的动图,看看不正交的情况下有什么不一样。
左乘 :
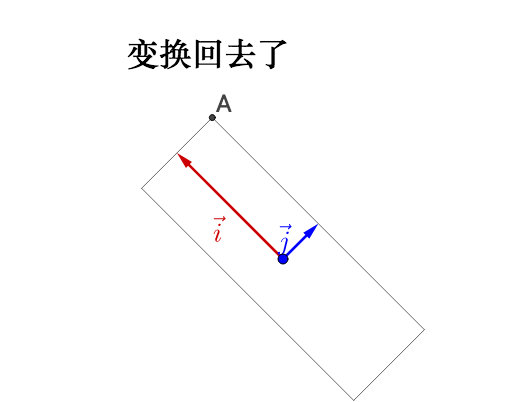
说明下,如果大家把这个文章和之前提到的我写的“相似矩阵”的文章参照来看的话,“相似矩阵”那篇文章里面我把图像的坐标系换了,所以看着图像没有变换(就好像直角坐标系到极坐标系下,图像是不会变换的)。而这里我把图像的坐标系给旋转、拉伸了,所以看着图像变换了(就好像换元,会导致图像变换)。这其实是看待矩阵乘法的两种视角,是等价的,但是显示到图像上就有所不同。
4 特征值、特征向量的应用
4.1 控制系统
之前的烧水系统是不稳定的。
的,系统最终会趋于稳定:
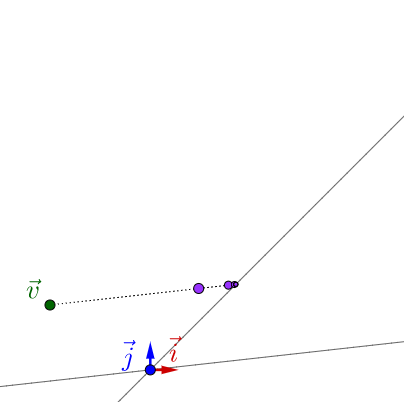
4.2 图片压缩
比如说,有下面这么一副的图片(方阵才有特征值,所以找了张正方形的图):

这个图片可以放到一个矩阵里面去,就是把每个像素的颜色值填入到一个的
矩阵中。
根据之前描述的有:
其中, 是对角阵,对角线上是从大到小排列的特征值。
我们在中只保留前面50个的特征值(也就是最大的50个,其实也只占了所有特征值的百分之十),其它的都填0,重新计算矩阵后,恢复为下面这样的图像:

效果还可以,其实一两百个特征值之和可能就占了所有特征值和的百分之九十了,其他的特征值都可以丢弃了。