2019独角兽企业重金招聘Python工程师标准>>> 
- 主成分分析(PCA)
a、一种降维技巧,将大量相关变量转化为一组很少的相关变量,这些 无关变量称为主成分
b、用一组较少的不相关变量代替大量相关变量,同时尽可能保留初始变量的信息,,推导所得到的变量称为主成分,它们是观测变量的线性组合,如第一主成分为:
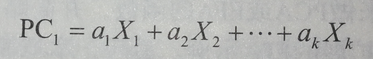
1、它是 k 个观测变量的加权组合,对初始变量集的方差解释性最大
2、第二主成分也是初始变量的线性组合,对方差的解释性排第二,同时与第一主成分正交(不相关),后面每一个主成分都最大化它对方差的解释程度,同时与之所有的主成分都正交
- 探索性因子分析(EFA)
a、一系列用来发现一组变量的潜在结构方法。他通过寻找一组更小,潜在的或隐藏的结构来解释已观测到的、显式的变量间的关系
b、EFA的目标是通过发掘隐藏在数据下的一组较少的,更为基本的无法观测的变量,来解释一组可观测变量的相关性。这些虚拟的、无法观测的变量称做因子(每个因子被认可解释多个观测变量间共有方差,因此准确来说,他们应该成为公共因子),模型的形式为
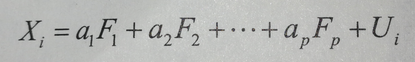
1、Xi是第 i 个可观测变量(i=1...k ),Fj 是公共因子(j=1...p),并且 p < k。Ui是 Xi变量独有的部分(无法被公共因子解释)
2、ai可认为是每个因子对复合而成的可观测变量的贡献值
- 两者的区别
主成分(PC1和PC2)是观测变量(X1和X5)的线性组合, 形成线性组合的权重都是通过最大化各主成分解释的方差来获得的,同时还要保证各主成分间不相关;
相反,因子(F1和F2)被当作观测变量的结构基础或“原因”,而不是线性组合。代表观测变量方差的误差(e1到e5)无法用因子来解释。图中的表示因子和误差无法直接观测,但可以通过变量间的相互关系推导得到,本例中,因子间带曲线的箭头表示它们之间有相关性。在EFA模型中,相关因子是常见的,但并不是必需的
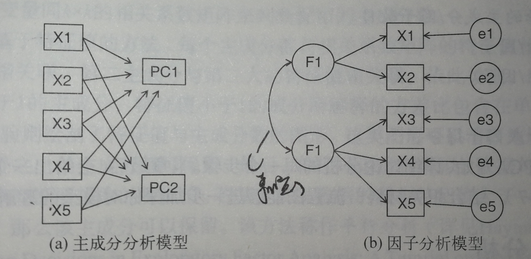
主成分分析和因子分析模型
注:
1、两种方法都需要大样本来支持稳定的结果,目前经验是:因子分析需要5-10倍于变量数的样本数
2、最近研究表明:所需样本量依赖于因子数目、与各因子相关联的变量数,以及因子对变量方差的解释程度
- psych包
R的基础安装包提供了 PCA 和 EFA 的函数,分别为 princomp() 和 factanal() ,但 psych包中有更好的函数
psych包中有用的因子分析函数
| 函数 | 描述 |
| principal() | 含多种可选的方差旋转方法的主成分分析 |
| fa() | 可用主轴、最小残差、加权最小平方或最大似然法估计的因子分析 |
| fa.parallel() | 含平行分析的碎石图 |
| factor.plot() | 绘制因子分析或主成分分析的结果 |
| fa.diagram() | 绘制因子分析或主成分的载荷矩阵 |
| scree() | 因子分析和主成分分析的碎石图 |
- PCA/EFA步骤
a、数据预处理
PCA 和 EFA 都根据观测变量间的相关性来推导结果,用户可输入原始数据矩阵或相关矩阵到 principal() 和 fa() 函数中。若输入初始数据,相关系数矩阵将会被动自动计算,在计算前请确保数据中没有缺失值
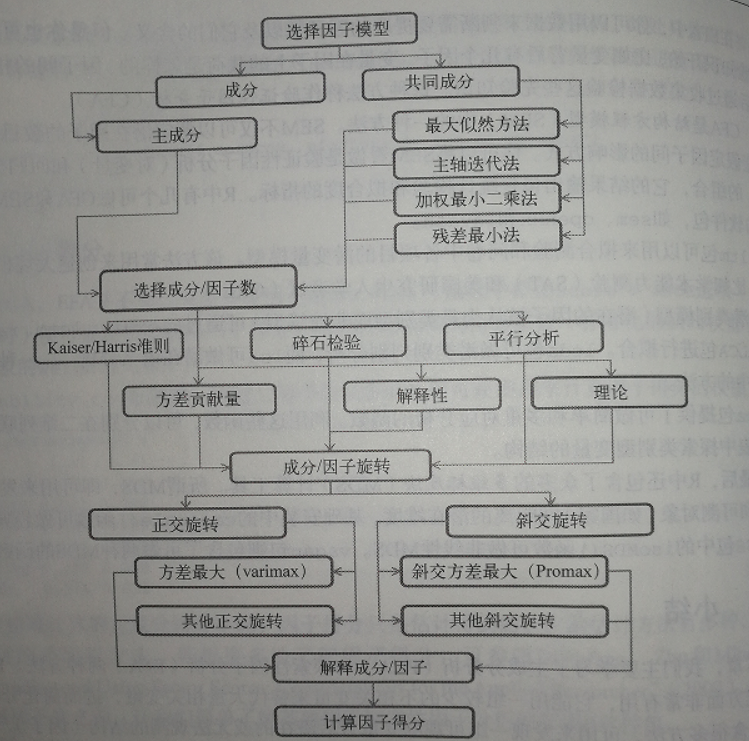
b、选择因子模型
判断是 PCA(数据降维)还是 EFA(发现潜在结构)更符合你的研究目标。如果选择 EFA 方法,你还需要选择一个估计因子模型方法(如最大似然估计)
c、判断要选择的主成分/因子数目
d、选择主成分/因子
e、旋转主成分/因子
f、解释结果
g、计算主成分或因子得分
R语言主成分和因子分析篇 - mousever的专栏 - CSDN博客
- 主成分/探索因子分析的分析步骤图