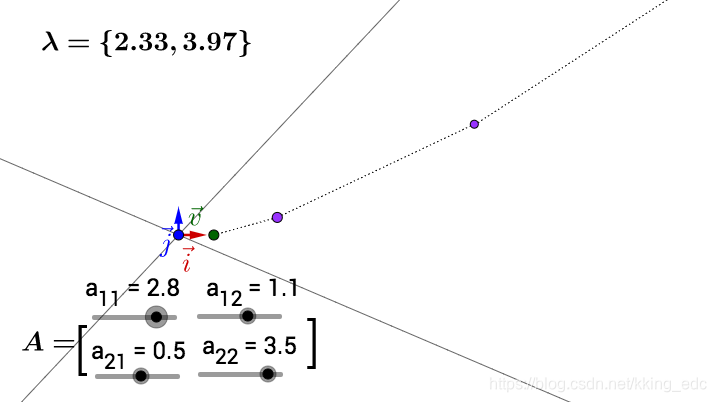
矩阵特征值

定义1：设A是n阶矩阵，如果数和n维非零列向量使关系式成立，则称这样的数成为方阵A的特征值，非零向量成为A对应于特征值的特征向量。

说明：1、特征向量，特征值问题是对方阵而言的。

　　　2、n阶方阵A的特征值，就是使齐次线性方程组有非零解的值，即满足方程的都是矩阵A的特征值。

　　　3、

 

定义2：A为n阶矩阵，称为A的特征矩阵，其行列式为的n次多项式，称为A的特征多项式，称为A的特征方程。

说明：1、由定义得，是A的特征值，等价于是其特征方程的根，因此又称为A的特征根。若是的重根，则称为A的重特征值（根）。

　　　2、方程的任意非零解向量，都是对应于的特征向量。

　　　3、A的特征矩阵也可以表示为；

　　　　  特征多项式也可以表示为；

　　　　  特征方程也可以表示为。

          4、求A的特征值就是求的根，求A的相应于的特征向量就是求的非零解向量。

求矩阵A的特征值及特征向量问题就转化为求解多项式方程以及齐次线性方程组的通解问题。

下面是一些练习：

例 求的特征值和特征向量

解 A的特征多项式为

　 

                                  

    所以A的特征值为，。

　当时，对应的特征向量应满足，

    即

　解得，所以对应的特征向量可取为。故相应于的全体特征向量为

    当时，由，即，解得，所以对应的特征向量可取为。故相应于的全体特征向量为

 

 

例 设，求A的特征值与特征向量。

解  ，

　　令得A的特征值为，。

　　当时，解方程。由得基础解系：，故对应于的全体特征向量为

　　当时，解方程。由，得基础解系为，，所以对应于的全部特征向量为： （，不同时为0）。

 

例 设，若3是A的一个特征值，求：y及A的其他特征向量。

解  设

　　因为3是A的一个特征值，所以3必为的根，因此求得y=2及的另一个根1，故A的全部特征值为-1，1，1，3

 

例 证明：若是矩阵A的特征值，x是A的属于的特征向量，则

　　（1）是的特征值（m是任意正整数）。

　　（2）当A可逆时，是的特征值。

证明：（1）

　　　　　　

　　　　　　再继续施行上述步骤m-2次，就得，故是矩阵的特征值，且x是对应于的特征向量。

　　　（2）当A可逆时，，由可得，故是矩阵的特征值，且x是对应于的特征向量。