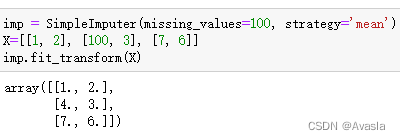
CSDN 的文档显示有一些问题,一些数学符号显示不正确,想看 word文档 的可以移步到 github : LearningDocuments/学习资料/平台无关/线性代数 at master · IceEmblem/LearningDocuments · GitHub
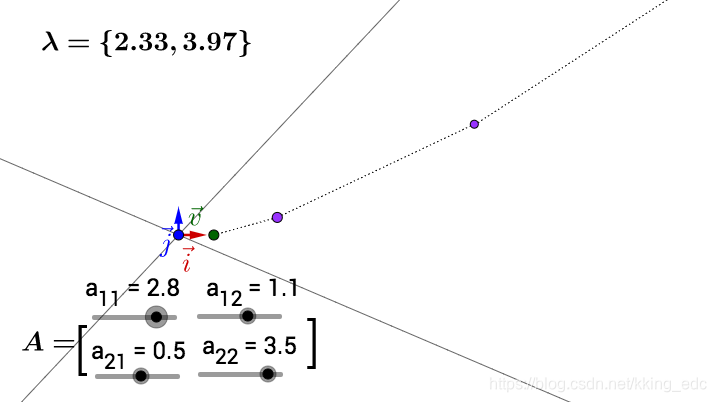
矩阵的特征值与特征向量
特征值与特征向量
对于n阶矩阵A,如果存在数值 λ 和非0向量 α,使得 Aα = λα ,则我们称 λ 为矩阵的特征值,α 为对应 λ 的特征向量
特征多项式
有等式Aα = λα 得出
λIα - Aα = 0
(λI - A)α = 0
(λI - A)是一个矩阵,α 是一个非0向量,这说明由矩阵 (λI - A) 表示的齐次线性方程组有非0解,则 |λI - A| = 0,根据该等式,我们可以求出 λ 的值
我们称 |λI - A| 为特征多项式
示例:求解特征值和特征向量
求解如下矩阵A的特征值和特征向量
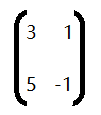
解:特征多项式 |λI - A| = 0为
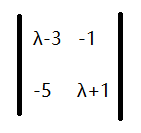
简化后得 (λ - 4)(λ + 2) = 0
得矩阵得特征值为 4 和 -2
我们将特征值4带入矩阵 (λI - A)
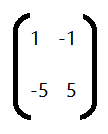
接下来就是利用增广矩阵求解基础解系,如果忘了请查阅线性方程组章节
得出对应得特征向量 α = (1, 1)T
同理将特征值-2带入矩阵中,求解对应得基础解系
多重特征值
n阶矩阵的特征多项式简化后为总会变为如下形式
左边是n个乘积右边是0
(λ - 4)(λ + 2)(λ - 1)(λ - 1) ... = 0
通过这个等式可以求出n个特征值,如 4,-2,1,1 ... ,有些特征值是相同的,如数值为1的特征值有2个,则我们将1这个特征值称为2重特征值
定理:n阶矩阵A与它的转置AT具有相同得特征值
证那么多干什么,我都记不住
定理:如果矩阵任何一行(或列)的所有元素aij的绝对值|aij|相加小于1,那么矩阵的所有 λ 的绝对值 |λ| 小于1
也就是说矩阵的每一行的所有元素的绝对值相加小于0,那么矩阵的 |λ| 都小于1
定理:n阶矩阵互不相同的特征值 λ1,λ2 ... λm 对应的特征向量 a1,a2 ... am 线性无关
定理:n阶矩阵的全部特征值相加等于矩阵的主对角线元素相加,而全部特征值相乘等于矩阵的行列式的值
如矩阵
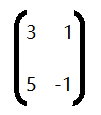
其特征值为 4,-2
4+(-2) = 2 + (-1)
4*(-2) = 3*(-1) - 5*1
相似矩阵与矩阵对角化
相似矩阵
如果存在非奇异矩阵P(即 |P| 不等于0)使得
P-1AP = B
则我们称A与B相似,记为 A~B
如下矩阵,A,B便是相似矩阵
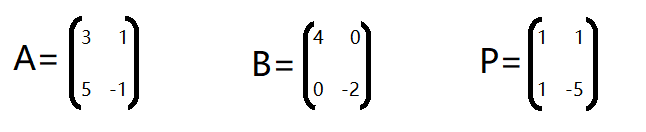
定理:如果矩阵A,B相似,则他们具有相同的特征值,相同的秩,相同的行列式值
定理:n阶矩阵A与其特征值λ1,λ2 ... λn组成的对角矩阵B相似的充分必要条件是特征值对应的特征向量a1,a2 ... am 线性无关
推论:如果n阶矩阵A其特征值λ1,λ2 ... λn没有重复值,则矩阵A与λ1,λ2 ... λn组成的对角矩阵相似
注意:就算有重复值,他们还是有可能相似
相似矩阵与特征值,特征向量的关系
如果过程可以让你了解相似矩阵与特征值,特征向量的关系
矩阵A有n个特征值 λ1,λ2 ... λn 和n个对应的特征向量 a1,a2 ... an ,我们设P = (a1,a2 ... an),B = 由 λ1,λ2 ... λn 组成的对角矩阵,则有
AP = A(a1,a2 ... an)
= (Aa1,Aa2 ... Aan)
= (λ1a1,λ2a2 ... λnan)

= PB
如果λ1,λ2 ... λn没有相同值,则a1,a2 ... an线性无关,则 |P| 不等于0,则P可逆
等式2边乘以P-1
P-1AP = P-1PB = IB = B
所以 A与B相似
约当块和约当形矩阵
如下,aii = λ,ai(i+1) = 1,其余元素均为0
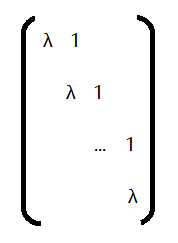
我们称这样的矩阵为约当块
如下矩阵
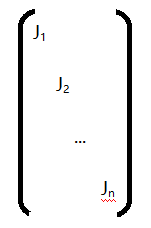
J1,J2,... Jn 都是分块矩阵,如果J1,J2,... Jn 都是约当块,那么我们称该矩阵为约当形矩阵
对于对角矩阵
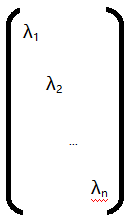
我们把每一个元素 λi 看作1阶约当块,所以对角矩阵也是约当形矩阵
定理:任意n阶矩阵A都与n阶约当形矩阵J相似
示例:
如下矩阵
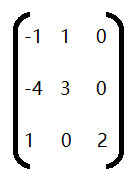
其特征值为 2,1,1,由其特征值组成的约当形矩阵如下
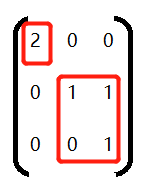
矩阵与其约当选矩阵相似
实对称矩阵的特征值和特征向量
实对称矩阵
对称矩阵中的元素均为实数
向量内积
n维向量 a = (a1, a2, ... an)T ,b = (b1, b2, ... bn)T
我们把 aTb (即 (a1, a2, ... an)(b1, b2, ... bn)T)称为向量内积
向量内积性质
aTb = bTa
(ka)Tb = kaTb
(a + b)Tc = aTc + bTc
aTa >= 0,仅当 a = 0 时,aTa = 0
向量长度
向量a的长度等于 √aTa (就是 根号 aTa 的值),记作 || a ||
示例:向量 a = (3, 4)T,其长度为 √ 32 + 42 = 5
如果你把向量 a 看作2维空间的一个点,那么它的长度就是原点(0, 0)T到该点的距离
向量长度的性质
|| a || >= 0,仅当 a = 0 时,|| a || = 0
|| ka || = |k| * || a ||
|aTb| <= || a || * || b ||
单位向量
长度为1的向量称为单位向量,对于任意非0向量a,其单位向量为
(1/|| a ||) a
正交向量
如果向量 a 与向量 b 内积等于 0,则称 a,b 相互正交(垂直)
正交向量组
如果非 0 向量组 a1,a2 ... an 两两相互正交,即任意的 aiTaj = 0,则称该向量组为正交向量组
定理:正交向量组线性无关
向量组正交化
线性无关向量组向量组 a1,a2 ... an 可以生成正交向量组 b1,b2 ... bn ,我们称为向量组正交化
如下生产a1,a2 ... an的正交向量组 b1,b2 ... bn
b1 = a1
b2 = a2 - ((a2Tb1)/(b1Tb1))*b1
b3 = a3 - ((a3Tb1)/(b1Tb1))*b1 - ((a3Tb2)/(b2Tb2))*b2
....
正交矩阵
如果n阶矩阵Q满足 QTQ = I 则称Q为正交矩阵
正交矩阵的性质
正交矩阵Q的行列式值为1或-1
正交矩阵Q的可逆矩阵 Q-1 = QT
如果 P,Q为正交矩阵,则 PQ 也是正交矩阵
定理:n阶实矩阵为正交矩阵的充分必要条件为其列(或行)向量组是单位正交向量组
单位正交向量组的意思是,向量组的向量是单位向量
定理:实对称矩阵不同特征值对应的特征向量相互正交
定理:设A为实对称矩阵,则存在正交矩阵Q使得Q-1AQ的结果为A特征值组成的对角矩阵
如果求解正交矩阵Q,如下
求出矩阵A特征值,求出对应特征值的特征向量组,将特征向量组正交化,将特征向量单位化,最后将这些特征向量组成正交矩阵Q
友好链接:https://blog.csdn.net/dabusidede/category_12233835.html