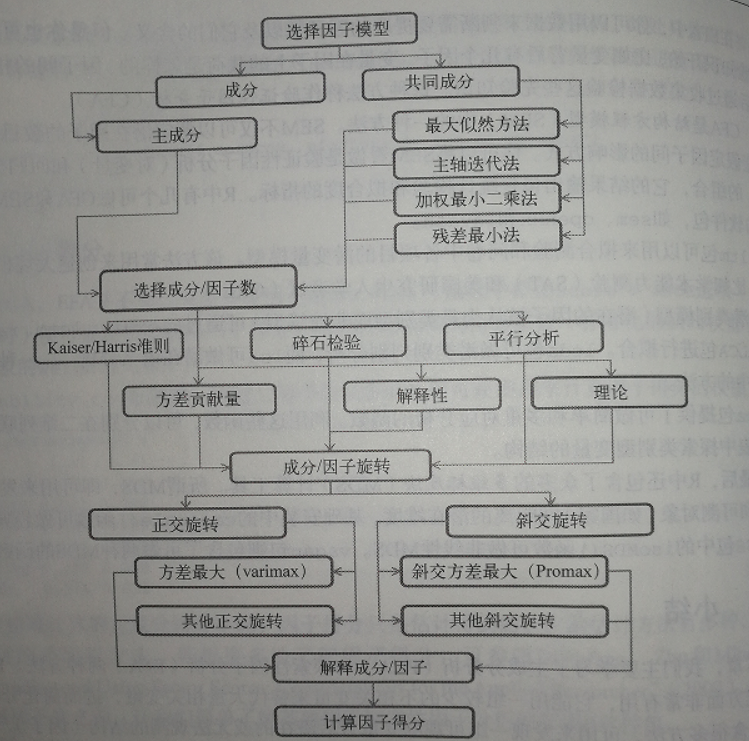
特征值分解
物理意义:
- 矩阵可以表示一种变换;
- 特征向量表示矩阵变换的方向;
- 特征值表示矩阵变换在对应特征向量方向上的变换速度;
特征值与特征向量
如下一个二维向量![]() ,这个二维空间的基向量是
,这个二维空间的基向量是![]() ;
;
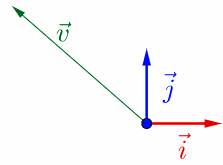
将向量![]() 左乘一个矩阵A,情况变成如下:
左乘一个矩阵A,情况变成如下:
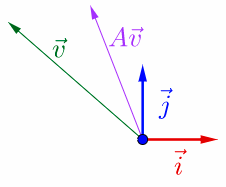
奇妙的来了,如果调整一下被乘的向量![]() 的方向到一个特定方向,则会出现如下情况
的方向到一个特定方向,则会出现如下情况

可以观察到,调整后的![]() 和
和![]() 在同一根直线上,只是
在同一根直线上,只是![]() 的长度相对
的长度相对![]() 的长度变长了。此时,我们就称
的长度变长了。此时,我们就称![]() 是A的特征向量,而
是A的特征向量,而![]() 的长度是
的长度是![]() 的长度的λ倍,λ就是特征值。
的长度的λ倍,λ就是特征值。
从而,特征值与特征向量的定义式就是这样的:

特征向量所在的直线上的所有向量都满足特征向量的上述定义,我们称其为特征空间。不过一般每个特征向量通常定义为一个单位向量(因为主要的意义是用来表示方向的)。
当然,一个矩阵通常不止一个特征向量,比如一个
n*n的矩阵最多有n个特征向量,每个特征向量之间相互正交,也有可能没有特征向量(求得时候发现方程无解或是复数)
意义
上面说了,特征向量表示矩阵变换的方向,特征值表示该方向上的变换速度。整个变换怎么理解呢?
我们可以这样想,每个矩阵在对一个向量做变换的时候,
- 首先将这个向量使用特征向量组成的正交基向量进行分解
- 然后目标向量在每个特征向量方向上的分量分别进行拉伸操作
- 对所有特征向量方向上的拉伸结果进行合并。
这个分解操作可以由下面的特征值分解进行解释
特征值分解其实是运动分解
一个矩阵进行特征值分解,这是一种将矩阵分解表示的操作。可以通过只保留比较重要的特征向量(将其他置为零)来压缩矩阵。
![]()
其中,
- V是n个特征向量组成的
n*n维矩阵 - D是n个特征值组成的一个对角矩阵(只有对角线上值不为0,维度也是
n*n) - 上面V与D中的特征向量与特征值是有序配对的,即第i个特征值对应第i个特征向量
使用一个具体例子进行解释如下:

如果使用这个矩阵对向量进行变换操作,我们会发现

特征值分解其实就是将矩阵的变换操作分解了,将旋转与拉伸分离开来,最后达到上述意义的效果。我们逐步解释
- 首先这是原本的基向量

- 左乘
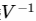 后,将原本的基向量进行了旋转,变换到矩阵特征向量上,即“将目标向量使用特征向量组成的正交基向量进行了分解”
后,将原本的基向量进行了旋转,变换到矩阵特征向量上,即“将目标向量使用特征向量组成的正交基向量进行了分解”

- 下面再左乘对角矩阵D,将目标向量在每个特征向量方向上的分量分别进行了拉伸操作

- 最后在左乘V,这个操作将基向量重新变换到原本的基向量上,即可以理解成”对所有特征向量方向上的拉伸结果进行合并”

总结
通过了解了整个特征值分解的意义,我们应该便能理解为什么说只对方阵进行特征值分解了。
这是因为只有方阵才能够在矩阵空间提取出符合完全正交基的特征向量,这样对于任何一个目标向量进行变换时,才能使用特征向量对目标向量进行完全表示。如果不能提取出满足条件的特征向量,则特征值分解的公式是不成立的!
那不能特征值分解时怎么办呢?我们可以使用奇异值分解
应用案例:压缩图像
如下有一幅512*512的灰度图像(只有方阵才能压缩)

这个图片可以放到一个矩阵里面去,就是把每个像素的颜色值填入到一个512×512的A矩阵中。 根据之前描述的有:
![]()
其中,D是对角阵,对角线上是从大到小排列的特征值。
我们在D中只保留前面50个的特征值(也就是最大的50个,其实也只占了所有特征值的百分之十),其它的都填0,重新计算矩阵后,恢复为下面这样的图像:

效果还可以,其实一两百个特征值之和可能就占了所有特征值和的百分之九十了,其他的特征值都可以丢弃了。
不过注意:在通过特征值分解的方式压缩过后,这个图像就不再是以前的图像了。