层次分析法(Analytic Hierarchy Process)
AHP是对一些较为复杂的,较为模糊的问题作出决策的简易方法,它特别适用于那些难以完全定量分析的问题。由美国运筹学家T.L.Saaty教授于上世纪70年代初期提出。
目录
层次分析法(Analytic Hierarchy Process)
一、建模步骤
二、层次结构模型
三、层次结构分析法的两个权重
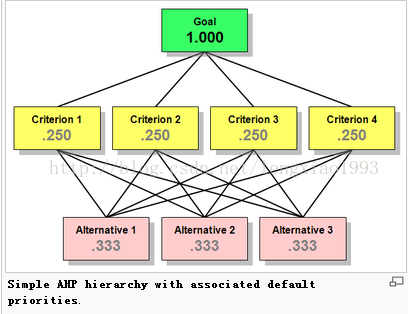
3.1 首先解决第一个问题:每个准则(因素)权重具体应该分配多少?
3.2 接下来解决第二个问题:每一个候选方案在每一个因素下又应该获得多少权重
总结
具体举例与代码
参考链接
一、建模步骤
运用层次分析法建模,大体上可按下面四个步骤进行:
- 建立递阶层次结构模型;
- 构造出各层次中的所有判断矩阵;
- 层次单排序及一致性检验;
- 层次总排序及一致性检验。
二、层次结构模型
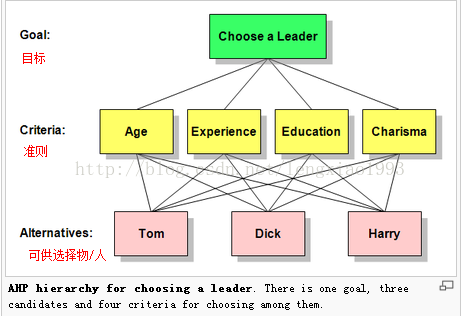
层次分析法是用来根据多种准则,或是说因素从候选方案中选出最优的一种数学方法
问题结构如图。首先做一个归一处理,给目标层(choose a leader)分配值为1或0,然后将这一值作为权重,分配给不同因素(Age,Experience,Education,Charisma),对应因素的权重大小代表该因素在整个选择过程中的重要性程度。
之后对于候选方案,每一个标准再将其权重值分配给所有的候选方案,每一方案获得权重值,来源于不同因素分得的权重值的和。最终获得的各个方案的的权重值的和依然为1。
例如选工作时,待遇所占的比重为0.8,有工作1,2,3候选, 如果工作1的待遇最高,工作2的待遇次之,工作3最差,则可将0.8的值按0.4,0.3,0.1分给工作1,2,3。
三、层次结构分析法的两个权重
从上文看,这不就是一个简单的权重打分的过程吗?为什么还要层次分析呢。这里就有两个关键问题:
- 每个准则Criterion的权重具体应该分配多少?
- 每一个候选方案Alternative在每一个因素下又应该获得多少权重?
这里便进入层次分析法的第二个步骤,也是层次分析法的一个精华: 构造比较矩阵(判断矩阵)Comparison Matrix
3.1 第一个问题:每个准则(因素)权重具体应该分配多少?
如果直接要给各个因素分配权重比较困难,但在不同因素之间两两比较其重要程度是相对容易的
将不同因素两两作比获得的值aij 填入到矩阵的 i 行 j 列的位置,则构造了所谓的比较矩阵,显然比较矩阵对角线上都是1, 因为是自己和自己比。这个矩阵容易获得,我们如何从这一矩阵获得对应的权重分配呢
这里需要引入概念,正互反矩阵和一致性矩阵
正互反矩阵定义:
我们目前构造出的矩阵很明显就是正互反矩阵。
一致性矩阵定义:
这里我们构造出的矩阵就不一定满足一致性,比如我们做因素1:因素2= 4:1 因素2:因素3=2:1 因素1:因素3=6:1(如果满足一致性就应该是8:1),我们就是因为难以确定各因素比例分配才做两两比较的,如果认为判断中就能保证一致性,就直接给出权重分配了。
一致性矩阵有一个性质可以算出不同因素的比例
重点:这里的w就是我们想要知道的权重,所以通过求比较矩阵的最大特征值所对应的特征向量,就可以获得不同因素的权重,归一化一下(每个权重除以权重和作为自己的值,最终总和为1)就更便于使用了。
注:我们给出的比较矩阵一般是不满足一致性的,但是我们还是把它当做一致矩阵来处理,也可以获得一组权重,但是这组权重能不能被接受,需要进一步考量。(即下文的一致性检验)例如在判断因素1,2,3重要性时,可以存在一些差异,但是不能太大,1比2重要,2比3 重要,1和3比时却成了3比1重要,这显然不能被接受。
一致性检验
当写出来判断矩阵之后还会存在一个问题,那就是按理来说如果i对j的重要程度是a,j对k的重要程度是b,那么理所应当i对k的重要程度应该a*b,有点符合“传递性”的感觉。但事实上不是这样的。所以需要进行一致性检验,如果在一定的合理范围之内,矩阵不需要修改,如果不在,则需要修改矩阵。
一致性的检验是通过计算一致性比例CR 来进行的
当 CR<0.10 时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正。
CI的值由判断矩阵计算获得,RI的值查表获得,具体的计算公式这里就略去,重点是理解为什么要做一致性检验。
3.2 第二个问题:每个候选方案在每个因素下又应该获得多少权重
这里则需要将不同候选方案,在不同因素下分别比较,具体的比较方法,还是使用比较矩阵,只不过之前准则层的比较矩阵比较的对象是因素,这里比较的是某一因素下,候选方案的优劣。
注:n个因素则需构造出来n个比较矩阵
例如在工作环境的因素下,工作1与工作2相比为 :4:2,工作2与工作3=2:1 ,工作1:工作3=6:1,这样构造一个矩阵,再用之前的一致性矩阵的方法就可以求出一个权重,然后相对应因素(这里是工作环境)所拥有的权值就可以按这个权重比例分配给不同候选物或人。
至此两个问题就都得到了解决。最终将每个候选物、人从不同因素获得的权值求和,就可以得到不同候选对于目标层的权值大小,继而可以根据值的大小,来选出优劣。
总结
通过对层次分析法的基本了解,不难发现层次分析法对人们的思维过程进行了加工整理,提出了一套系统分析问题的方法,为科学管理和决策提供了较有说服力的依据。
明显的缺点是,整个分析过程似乎都是依赖于人的主观判断思维,一来不够客观,二来两两比较全部人为完成,还是非常耗费精力的,尤其是当候选方案比较多的时候。
具体举例与代码
有一个毕业生为挑选合适的工作。经双方恳谈,已有三个单位表示愿意录用某毕业生,该毕业生考虑的因素有6个,研究课题、发展前途、待遇、同事情况、地理位置和单位名气。
那么这六个因素就是准则层,三个单位就是方案层,最后要求的就是应该去哪个单位。
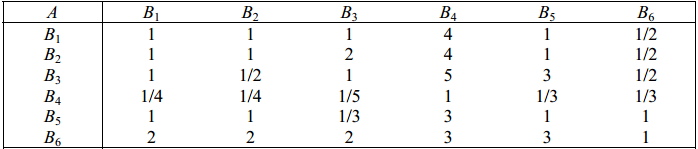
1)准则层判断矩阵(主观性)
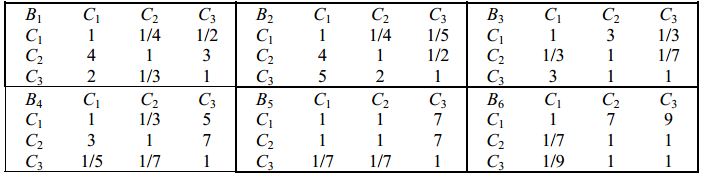
2)方案层判断矩阵(主观性)
分别针对每一个B,判断C1、C2、C3之间的相对大小
计算的 Matlab 程序如下:
clc,clear
fid=fopen(‘txt3.txt’,’r’);
n1=6;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp]; %读准则层判断矩阵
end
for i=1:n1
str1=char([‘b’,int2str(i),’=[];’]);
str2=char([‘b’,int2str(i),’=[b’,int2str(i),’;tmp];’]);
eval(str1);
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2); %读方案层的判断矩阵
end end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1
[x,y]=eig(eval(char([‘b’,int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0
纯文本文件txt3.txt中的数据格式如下:
1 1 1 4 1 1/2
1 1 2 4 1 1/2
1 1/2 1 5 3 1/2
1/4 1/4 1/5 1 1/3 1/3
1 1 1/3 3 1 1
2 2 2 3 3 1
1 1/4 1/2
4 1 3
2 1/3 1
1 1/4 1/5
4 1 1/2
5 2 1
1 3 1/3
1/3 1 1/7
3 7 1
1 1/3 5
3 1 7
1/5 1/7 1
1 1 7
1 1 7
1/7 1/7 1
1 7 9
1/7 1 1
1/9 1 1
R语言中AHP的应用参考
https://cran.r-project.org/web/packages/ahpsurvey/vignettes/my-vignette.html
参考与资源
[1]《数学建模算法与应用》
[2] https://blog.csdn.net/lengxiao1993/article/details/19575261
[3]https://blog.csdn.net/fz_851474/article/details/52281849


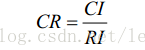











![[h5]一个基于HTML5实现的视频播放器代码详解](https://common.cnblogs.com/images/copycode.gif)