学习目标

1. 理解使用DESeq2差异表达分析过程中的不同步骤
2. 探讨离散度在差异表达分析中的重要性，并利用离散度值的图来探讨NB模型的假设

DESeq2差异基因表达分析流程

之前，我们使用适当的设计公式创建了DESeq2对象，并使用两行代码运行DESeq2:

# DO NOT RUN## Create DESeq2Dataset object
dds <- DESeqDataSetFromTximport(txi, colData = meta, design = ~ sampletype)## Run analysis
dds <- DESeq(dds)

我们用DESeq2完成了差异基因表达分析的整个工作流程。分析中的步骤输出如下:

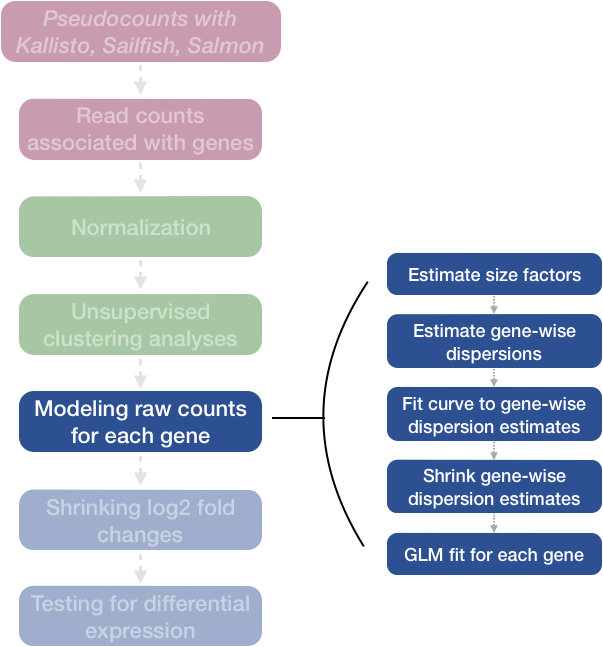
我们将详细查看每一个步骤，以更好地理解DESeq2是如何执行统计分析的，以及我们应该检查哪些度量来探究我们的分析质量。

第一步：估计大小因子

差异表达分析的第一步是估计大小因子，这正是我们已经对原始计数进行归一化所做的。

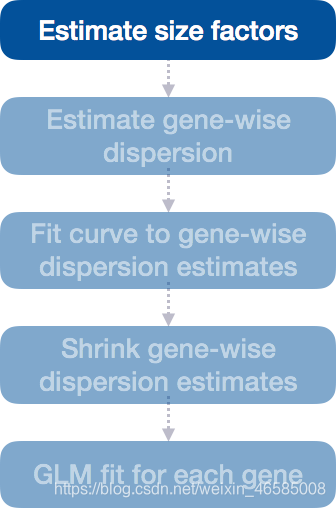
当执行差异表达分析时，DESeq2将自动估计大小因子。但是，如果你已经使用estimateSizeFactors()生成了大小因子，就像我们前面所做的那样，那么DESeq2将使用这些值。
为了归一化计数数据，DESeq2使用先前在“计数归一化”课上讨论的比值中位数方法计算每个样本的大小因子。
MOV10 DE分析:检查大小因子
让我们快速看一下每个样本的大小因子值:

## Check the size factors
sizeFactors(dds)Irrel_kd_1 Irrel_kd_2 Irrel_kd_3 1.1150371  0.9606366  0.7493552 
Mov10_kd_2 Mov10_kd_3 Mov10_oe_1 1.5634128  0.9359082  1.2257749 
Mov10_oe_2 Mov10_oe_3 1.1406863  0.6541689

这些数字应该与我们在运行函数estimateSizeFactors(dds)时最初生成的数字相同。看看每个样本的读段总数:

## Total number of raw counts per sample
colSums(counts(dds))Irrel_kd_1 Irrel_kd_2 Irrel_kd_3 31160785   26504972   20498243 
Mov10_kd_2 Mov10_kd_3 Mov10_oe_1 45300696   26745860   32062221 
Mov10_oe_2 Mov10_oe_3 30025690   17285401 

这些数字与大小因子的关系是什么?

我们看到较大的大小因子对应于序列深度较高的样本，这是有意义的，因为要生成归一化的计数，我们需要将计数除以尺寸因子。这就解释了样品间测序深度的差异。

现在看一看归一化后的总深度，使用以下代码:

## Total number of normalized counts per sample
colSums(counts(dds, normalized = TRUE))Irrel_kd_1 Irrel_kd_2 Irrel_kd_3 27945962   27591050   27354509 
Mov10_kd_2 Mov10_kd_3 Mov10_oe_1 28975519   28577441   26156696 
Mov10_oe_2 Mov10_oe_3 26322477   26423452

样本间的值如何与每个样本的总计数进行比较?
你可能期望经过归一化后，各个样本的计数是完全相同的。然而，在归一化过程中，DESeq2也解释了RNA的组成。通过使用大小因子的中位数比值，DESeq2不应该偏向于由几个DE基因吸收的大量计数；然而，这可能导致大小因子与仅仅根据测序深度预期的大小因子有很大的不同。

第二步：估计基因离散（gene-wise dispersion）

差异表达分析的下一步是对基因离散的估计。在讨论细节之前，我们应该对DESeq2中离散指的是什么有一个很好的概念。

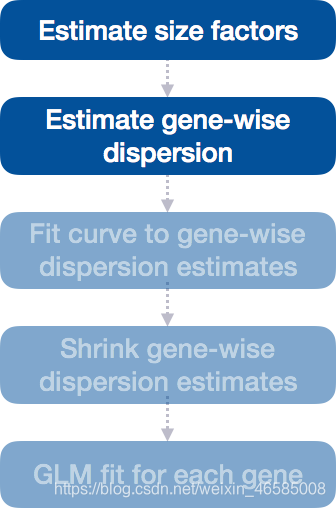
在RNA-seq计数数据中，我们知道:

1. 为了确定差异表达基因，考虑到组内(重复样本之间)的差异，我们需要识别组间平均表达显著不同的基因。
2. 组内(重复样本之间)的变异需要考虑到方差随平均表达值增加的事实，如下图所示(每个黑点是一个基因)。

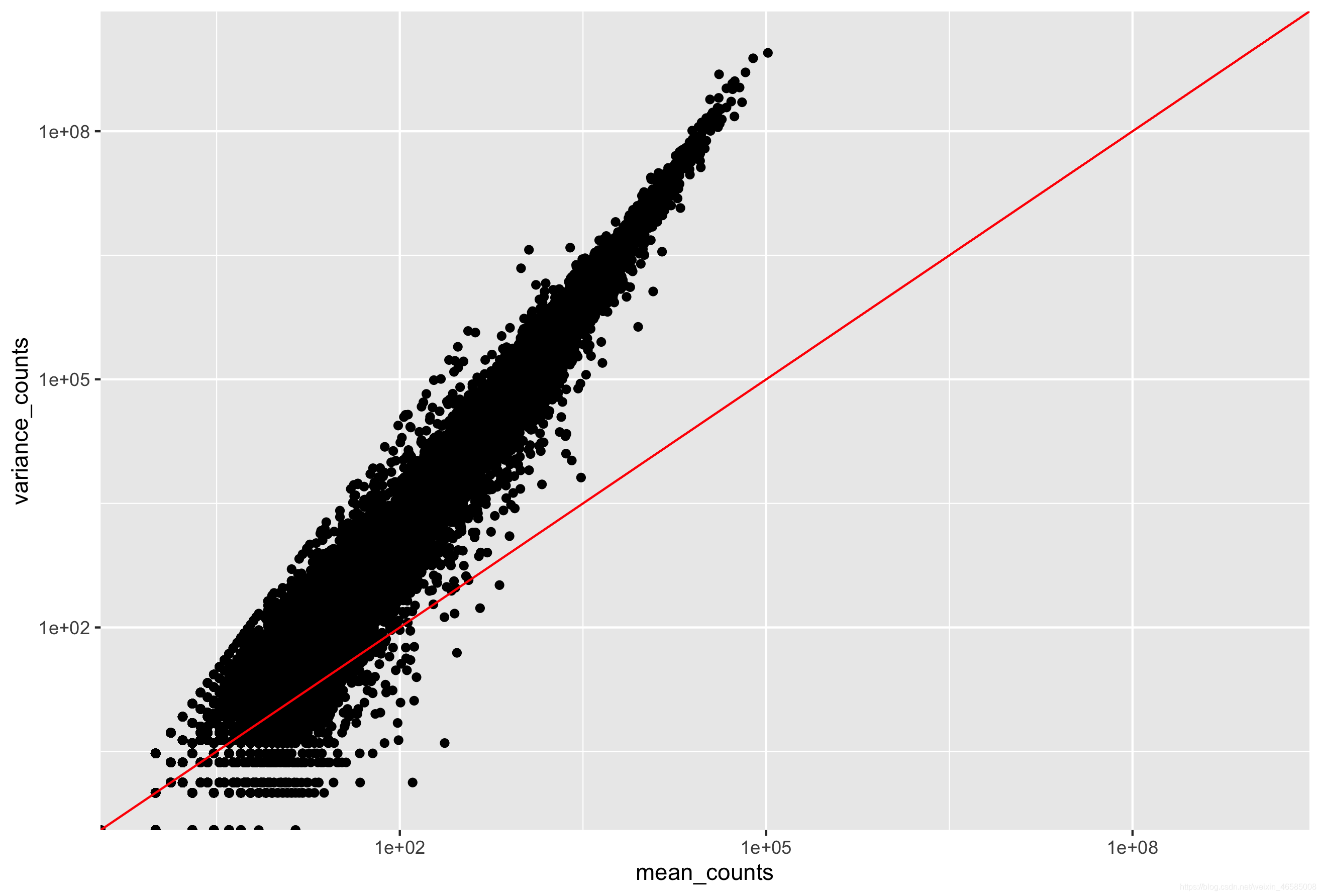
为了准确地识别DE基因，DESeq2需要解释方差与均值之间的关系。 我们不希望所有的DE基因都是低计数的基因，因为低表达基因的方差更低。
DESeq2没有使用方差作为数据中变异的度量衡(因为变异与基因表达水平相关)，而是使用离散度（dispersion） 作为变异度量衡，它解释了基因的变异和平均表达水平。离散度的计算方法为Var = μ + α*μ^2，其中:α = dispersion, Var = variance, 和 μ = mean，有以下关系：

	对离散的影响
方差增加	离散增加
平均表达增加	离散减少

对于具有中等到高计数值的基因，离散度的平方根将等于变异系数（ \sqrtα=\frac{σ}{μ} ）。因此，0.01的离散度意味着在生物重复中围绕平均数预期的10%的变异。具有相同平均数的基因的离散度估计将仅基于其方差而有所不同。因此，离散度估计（dispersion estimates）反映了给定平均值的基因表达的方差。在下面的图中，每个黑点都是一个基因，离散度与每个基因的平均表达量（组内重复）作对比。

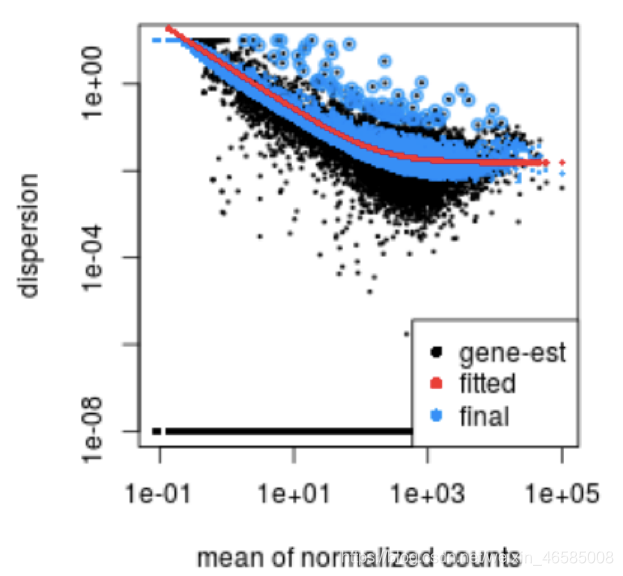
离散和我们的模型有什么关系?
为了精确地建立测序计数模型，我们需要对每个基因的组内变异(同一样本组重复之间的变异)做出准确的估计。由于每组只有少量(3-6)重复，对每个基因变异的估计往往是不可靠的。
为了解决这个问题，DESeq2共享基因间的信息，通过一种叫做“收缩（shrinkage）”的方法，基于基因的平均表达水平，产生更准确的变异估计。DESeq2假设具有相似表达水平的基因应该具有相似的离散度。

分别估计每个基因的离散度:
DESeq2根据基因的表达水平(组内重复的平均计数)和方差估计每个基因的离散度。

第三步：拟合曲线到基因的分散估计

工作流程的下一步是拟合曲线到基因分散估计。拟合数据曲线背后的想法是，不同的基因会有不同程度的生物变异，但是，在所有的基因中，会有一个合理的分散估计分布。

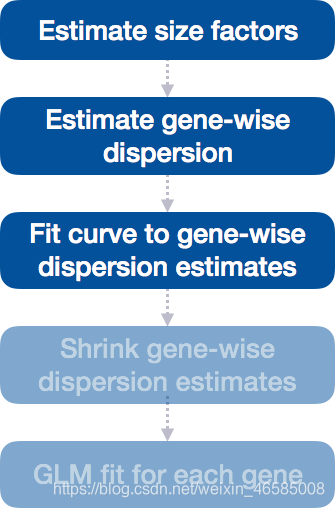
下图中这条曲线以红线表示，它绘制了给定表达强度基因的预期离散的估计值。每个黑点都是一个基因，具有相关的平均表达水平和离散度的最大似然估计(MLE)(步骤1)。

第四步:将基因离散估计值向曲线预测值收缩

工作流程的下一步是将基因离散估计值向曲线预测值收缩。

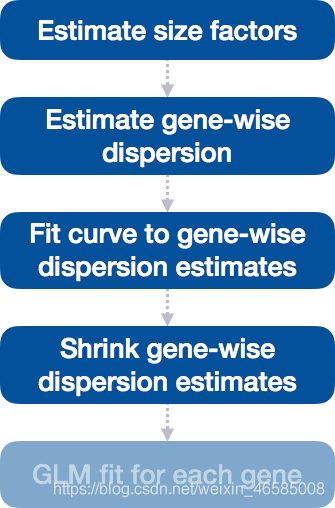
当样本量较小时，曲线可以更准确地识别差异表达的基因，每个基因的收缩强度取决于:

• 基因的离散度距离红色曲线的距离
• 样本量（样本量越大，则收缩的越少）

这种收缩方法对于减少差异表达分析中的假阳性尤其重要。 具有低离散度估计数的基因向曲线收缩，并且更精确、更大的收缩值被输出用于模型拟合和差异表达检验。这些缩小后的估计值代表了组内的变异，需要确定是否组间的基因表达有显著差异。
稍微高于曲线的离散估计也向曲线收缩，以便更好地估计离散；然而，具有极高离散值的基因则不收缩。这是由于该基因可能没有遵循建模假设，并且由于生物学或技术原因比其他基因具有更高的变异性[1]。向曲线方向收缩估计值可能会导致假阳性，所以这些值不会被收缩。这些基因被下面的蓝色圆圈所包围。

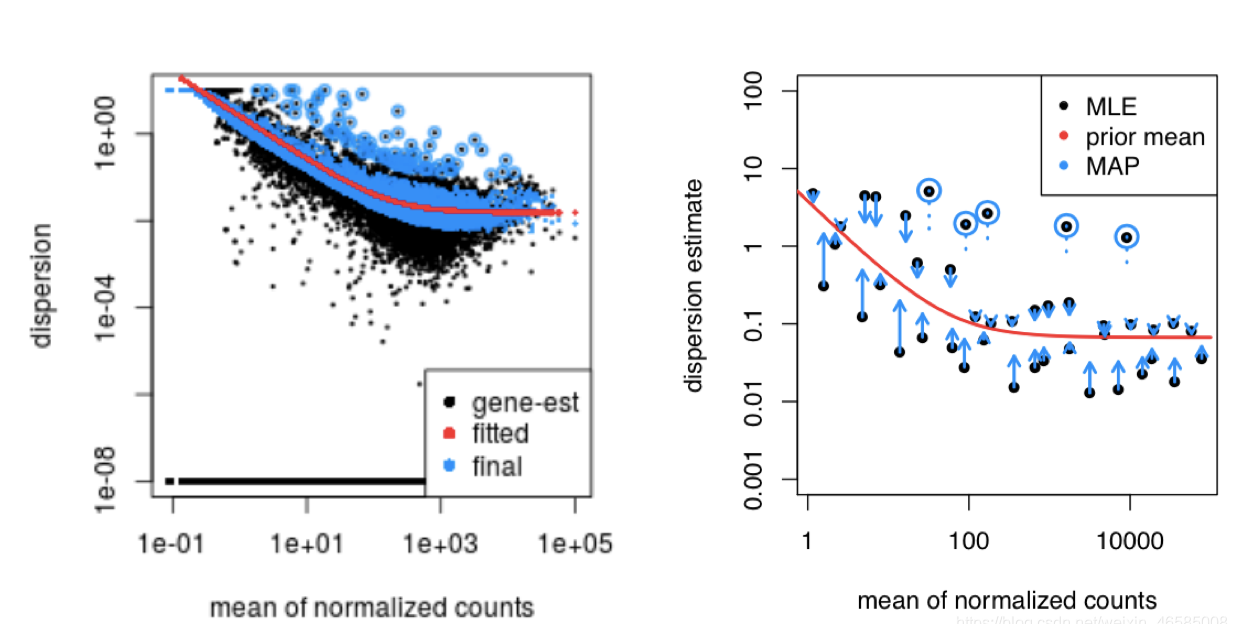
这是一个很好的绘图，可以确保你的数据很好的拟合DESeq2模型。你希望你的数据通常散布在曲线周围，随着平均表达水平的增加，离散度逐渐减小。如果你看到一片云（cloud）或不同的形状，那么你可能想要更深入探索你的数据，看看你是否有污染(线粒体等)或离群样本。请注意，对于任何低自由度的实验，在plotdispest()图中整个平均值范围的收缩程度。
令人不安的离散曲线（worrisome dispersion plots） 的例子如下:
下面的图显示了分散值的云，它们通常不遵循曲线。这将令人担忧，并表明数据与模型不符。

下一张图显示，离散度值先减小，然后随着表达值的增大而增大。根据我们的预期，较大的平均表达式值不应该有较大的离散度——我们希望离散度随着均值的增加而减少。这表明高表达基因的变异比预期的要少。这也表明在我们的分析中可能存在一个离群样本或污染。

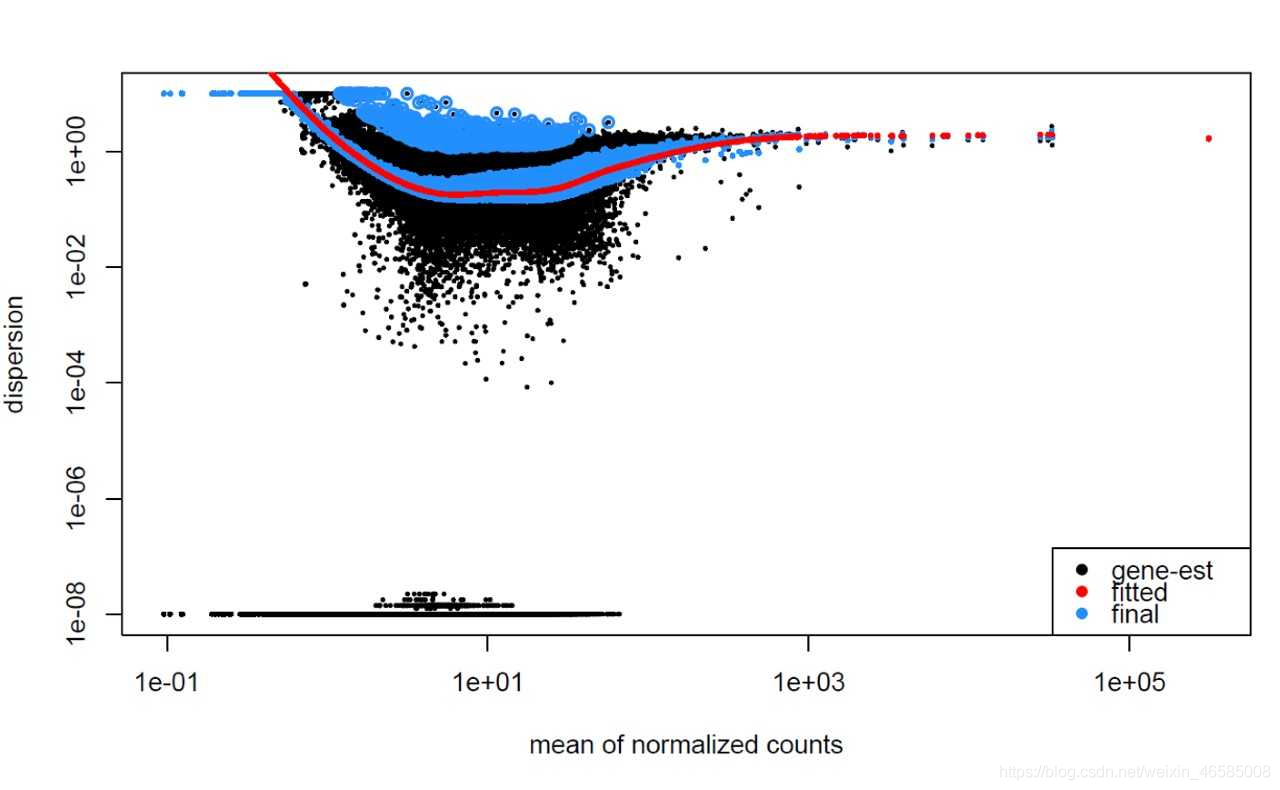
MOV10 DE分析:探讨离散估计和评估模型拟合

让我们来看看我们的MOV10数据的离散估计:

## Plot dispersion estimates
plotDispEsts(dds)

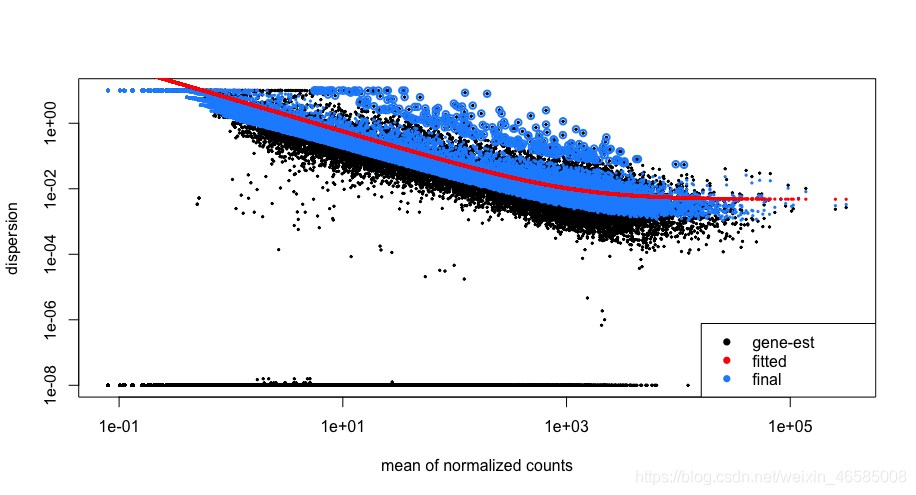
由于我们的样本量较小，对于许多基因我们看到了相当大的收缩。你认为我们的数据能很好地拟合这个模型吗?
我们看到随着平均表达的增加离散度很好地降低了，这很好。我们还可以看到离散估计通常围绕曲线，这也是预期的。总的来说，这个图看起来不错。我们确实看到了强烈的收缩，这可能是由于我们的一个样本组只有两个重复的事实。我们拥有的重复越多，应用于离散估计的收缩就越少，可以识别的DE基因就越多。为了更好地估计变异，我们一般建议每个条件至少有4个生物重复。

---

Exercise

Given the dispersion plot below, would you have any concerns regarding the fit of your data to the model?

• If not, what aspects of the plot makes you feel confident about your data?
• If so, what are your concerns? What would you do to address them?

---

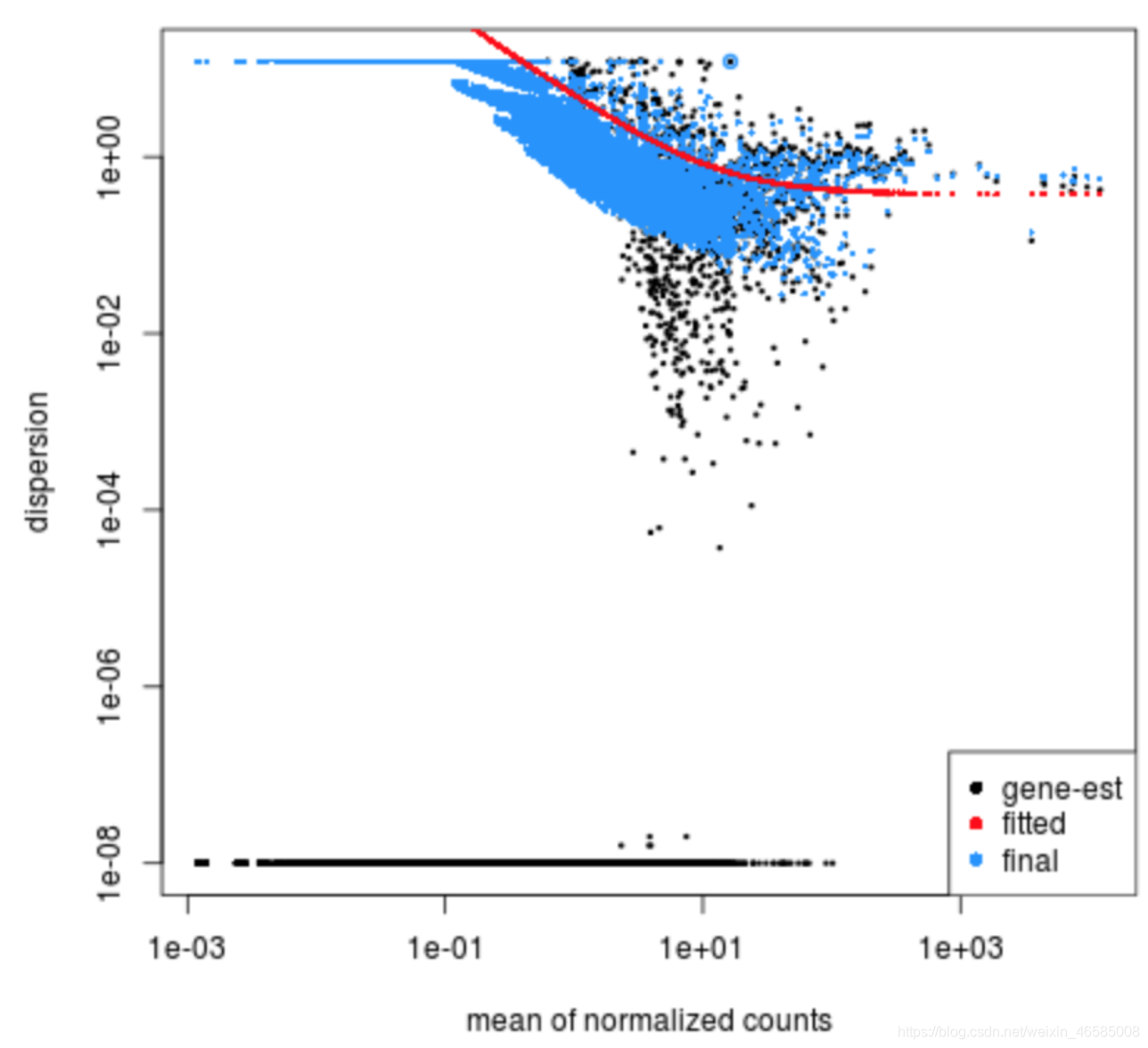
Answer

# Ans: Yes, there are some concerns. The data does not scatter around the fitted curve, and the distribution of normalized counts are restricted in a small range. I would double check QC of my samples to make sure that there are no contamination or outliers.

---