1 原理

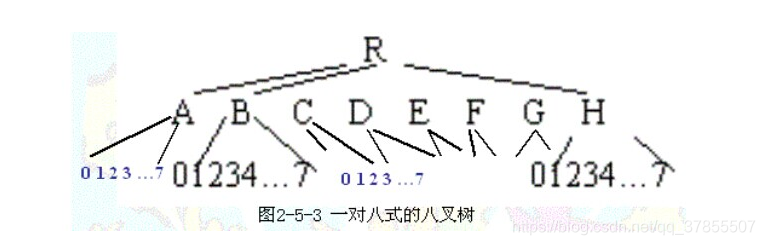
八叉树其实是一种特殊的由上至下的体素，其构造原理在这里不再进行赘述，详细的构造方式可参考博客：https://blog.csdn.net/qq_32867925/article/details/109094719

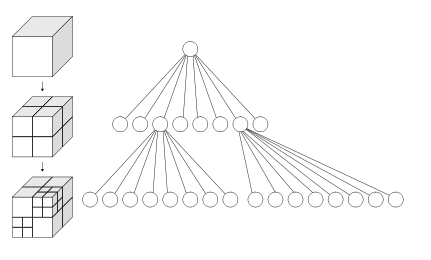
有时候为了将点云、构造的层次八叉树需要进行可视化，便于人理解以及检查构造八叉树是否合理。如下图示，可以看见其构建了2次八叉树，即蓝色框和黄色框所示，每一个体素内包含的点各不相同。更多层次的八叉树，如3层、4层等都是类似的。

2 可视化

PCL支持将上述可视化结果进行显示，下面代码示例了其可视化过程，也包括了八叉树的构建，但侧重于如何将八叉树进行可视化。

//可视化体素
void main()
{IO IOject;char *inputpath = "test.txt";//char *inputpath = "D:\\LL\\individual_build.txt";vector<pcl::PointXYZ> cloud = IOject.ReadPointXYZIntoVector(inputpath);vector<grid> gridcluster;double gridsize = 2.5;gridpoint(cloud, gridcluster, gridsize);//gridcluster 为格网化后的点集vector<Cubic>allcubic;vector<vector<pcl::PointXYZ>> multisegs;for (int i = 0; i < gridcluster.size(); i++){if (gridcluster[i].points.size()>0){pcl::PointXYZ leftbottom, rightup;GetMinBoundingCubic(gridcluster[i].points, leftbottom, rightup);OctreeNode *root = new OctreeNode();BuildOctree(root, leftbottom, rightup, gridcluster[i].points, 0.05);vector<Cubic> cubics;GetleafCubic(root, cubics);for (int k = 0; k < cubics.size(); k++){allcubic.push_back(cubics[k]);}//再添加点云数据vector<vector<pcl::PointXYZ>> planecluster, nonplanecluster;FalseCluster(root, planecluster, nonplanecluster);for (int j = 0; j < planecluster.size(); j++){multisegs.push_back(planecluster[j]);}}}pcl::visualization::PCLVisualizer viewer("voxel viewer");viewer.setBackgroundColor(0, 0, 0);struct myRGB{myRGB(double a, double b, double c){this->R = a;this->G = b;this->B = c;}double R;double G;double B;};vector<myRGB> colors;myRGB c1(255, 0, 0), c2(0, 255, 0), c3(0, 0, 255), c4(255, 255, 0), c5(0, 255, 255);for (int i = 0; i < allcubic.size(); i++){stringstream ss;ss << i + 1;string str;ss >> str;double length = allcubic[i].Upright.x - allcubic[i].Buttomleft.x;if (length < gridsize/16){viewer.addCube(allcubic[i].Buttomleft.x, allcubic[i].Upright.x, allcubic[i].Buttomleft.y, allcubic[i].Upright.y, allcubic[i].Buttomleft.z, allcubic[i].Upright.z, c1.R, c1.G, c1.B, str, 0);}else if (length >= gridsize / 16 && length < gridsize/8){viewer.addCube(allcubic[i].Buttomleft.x, allcubic[i].Upright.x, allcubic[i].Buttomleft.y, allcubic[i].Upright.y, allcubic[i].Buttomleft.z, allcubic[i].Upright.z, c2.R, c2.G, c2.B, str, 0);}else if (length >= gridsize / 8 && length <gridsize/4){viewer.addCube(allcubic[i].Buttomleft.x, allcubic[i].Upright.x, allcubic[i].Buttomleft.y, allcubic[i].Upright.y, allcubic[i].Buttomleft.z, allcubic[i].Upright.z, c3.R, c3.G, c3.B, str, 0);}else if (length >= gridsize / 4 && length < gridsize/2){viewer.addCube(allcubic[i].Buttomleft.x, allcubic[i].Upright.x, allcubic[i].Buttomleft.y, allcubic[i].Upright.y, allcubic[i].Buttomleft.z, allcubic[i].Upright.z, c4.R, c4.G, c4.B, str, 0);}else{viewer.addCube(allcubic[i].Buttomleft.x, allcubic[i].Upright.x, allcubic[i].Buttomleft.y, allcubic[i].Upright.y, allcubic[i].Buttomleft.z, allcubic[i].Upright.z, c5.R, c5.G, c5.B, str, 0);}viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, str);//viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_LUT_HSV, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, str);}//  addCube (float x_min, float x_max, float y_min, float y_max, float z_min, float z_max,//double r = 1.0, double g = 1.0, double b = 1.0, const std::string &id = "cube", int viewport = 0);srand((int)time(0));for (int i = 0; i < multisegs.size(); i++){pcl::PointCloud<pcl::PointXYZ>::Ptr cloudptr(new pcl::PointCloud<pcl::PointXYZ>);cloudptr = IOject.PointXYZ2Ptr(multisegs[i]);stringstream ss;ss << i + 1000;string str;ss >> str;int R = rand() % 255;int G = rand() % 255;int B = rand() % 255;pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> single_color(cloudptr, R, G, B);//第二个平面颜色设置成蓝色 single_color_02viewer.addPointCloud<pcl::PointXYZ>(cloudptr, single_color, str);//将single_color在viewer中进行显示viewer.setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 5, str);}while (!viewer.wasStopped()){viewer.spinOnce(1);}}