松散八叉树

article/2025/10/28 23:30:29

1八叉树简述
- 1.1定义
- 1.2数据
- 1.3树的建立
  - 1.3.1计算包围体的大小与中心点
  - 1.3.2判断物体所属的包围盒
2松散八叉树
- 2.1松散八叉树的建立

八叉树简述

定义

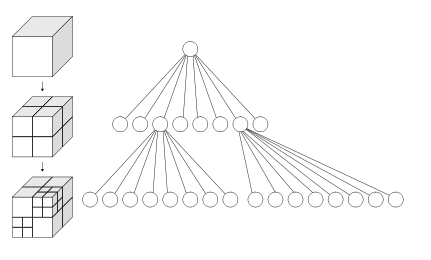
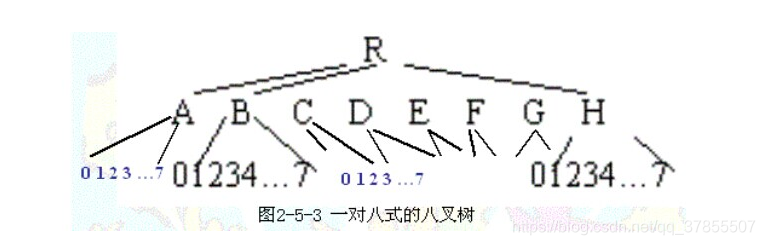
八叉树是一种对三维世界进行场景管理的理想的空间数据结构。八叉树中根节点包含一个立方体包围盒。每个非叶子节点都拥有八个子节点，它们将双亲节点细分为八分体。也就是说而且每个子节点表示一个立方体的体积元素，而且所有子节点的体积加起来是父节点的体积。
当满足用户所定义的标准被满足时，停止细分。常见的停止标准有：

节点包围盒达到一个特定大小
节点内包含的多边形数目达到最小数目

数据

八叉树的每个节点至少要包含以下数据：

包围盒 — 空间中的八叉树节点所包含的封闭立方体
几何体列表 — 包含在该节点内的所包含的几何体
子节点 — 指向每个子节点的指针
相邻节点 — 每个节点最多有六个相邻节点（立方体拥有六个平面）。在碰撞检测的过程中，对八叉树的遍历要求指向相邻节点的指针。

树的建立

包含多边形数目大于最低阈值POLY_THRESHOLD的节点，BuildOctree()会产生8个子节点。BuildNode()函数创建了节点数据，主要包含两个步骤：

为节点创建包围盒（通过父节点的包围盒确定宽度、高度以及深度，并通过索引i确定包围盒的中心位置是8个子节点中的哪一个）
确定哪些多边形位于节点的包围盒内部

BuildOctree(Node N) { if(NumPolys(N)>POLY_THRESHOLD) for(int i = 0; i < 8; i++) { BuildNode(N->Child[i], i, N); BuildOctree(N->Child[i]); } }

BuildOctree(Node N)

{

if(NumPolys(N)>POLY_THRESHOLD)

for(int i = 0; i < 8; i++)

{

BuildNode(N->Child[i], i, N);

BuildOctree(N->Child[i]);

}

计算包围体的大小与中心点

某层节点立方体包围盒的边长计算公式：

L(depth)=W/(2depth)

某层节点与其相邻节点包围盒中心间距的计算公式：

S(depth)=W/(2depth)

W:worldsize

depth:depth(root)=0

判断物体所属的包围盒

伪代码如下：

struct node{ vector3 CubeCenter; node* Child[2][2][2]; ObjectList Objects; }; int Classify(plane p,volume v){ if(v is completely behind p){ return 0; }else if(v is completely in front of p){ return 1; }else{ // v straddles p. return 2; } } void InsertObjectIntoTree(node* n,Object* o){ int xc = Classify(plane(1,0,0,CubeCenter.x)),o.BoundingVolume); int yc = Classify(plane(0,1,0,CubeCenter.y)),o.BoundingVolume); int zc = Classify(plane(0,0,1,CubeCenter.z)),o.BoundingVolume); if(xc ==2 || yc == 2 || zc == 2) { //Object straddles one pr more of the child partition planes, //and so won't fit in any child node,so store it in this node. Objects.Insert(o) }else{ //Object fits in one of the child nodes.Recurse to find the //correct descendant. InsertObjectIntoTree(Child[zc][yc][xc],o) } }