浮点数在计算机中如何用二进制存储？

前言

前面我有篇博文详解了二进制数，以及如何同二进制数表示整数。但是，计算机处理的不仅仅是整数，还有小数，同样小数在计算机也是用二进制进行存储的，但是，二进制如何去存储小数呢？计算机对于小数的计算又是否真的丝毫不差呢？本文将进行介绍。

一、用二进制表示小数

二进制转换为十进制的方法就是各个位的数字与位权乘积之和。二进制数小数点前面部分的位权，第 1 位是 2 的 0 次幂、第 2 位 是 2 的 1 次幂……以此类推。小数点后面部分的位权，第 1 位是 2 的－1次幂、第2位是2的－2次幂。以此类推。0次幂前面的位的位权 按照 1 次幂、2 次幂……的方式递增，0 次幂以后的位的位权按照－1 次幂、－2次幂……的方式递减。这一规律并不仅限于二进制数，在十 进制数和十六进制数中也同样适用。
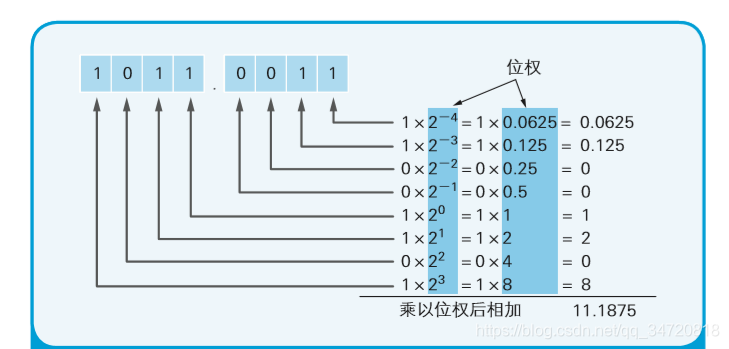
如把1011.0011这个有小数点的二进制数转换成十进制数过程如下：

二、计算机并不是永远准确的

我们可以很快算出，0.1累加100次后的结果是10，但是计算机算出来结果是10吗？实际上它计算出的结果是10.0000002

#include <stdio.h>void main(){ float sum;      
int i;
// 将保存总和的变量清 0    
sum = 0;
//0.1 相加 100 次   
for (i = 1;  i <= 100; i++) 
{        sum += 0.1f;
}
// 显示结果  
printf("%f\n", sum); }

• 那么，这是为什么呢？计算机为什么会出错呢？道理也很简单，就如我们现实生活中使用的十进制数，有些数字我们也不能精确计算出来，比如1/3；同样，计算机用二进制表达数字，有些小数二进制也无法精确表达，比如十进制数0.1就无法用二进制数正确表达。

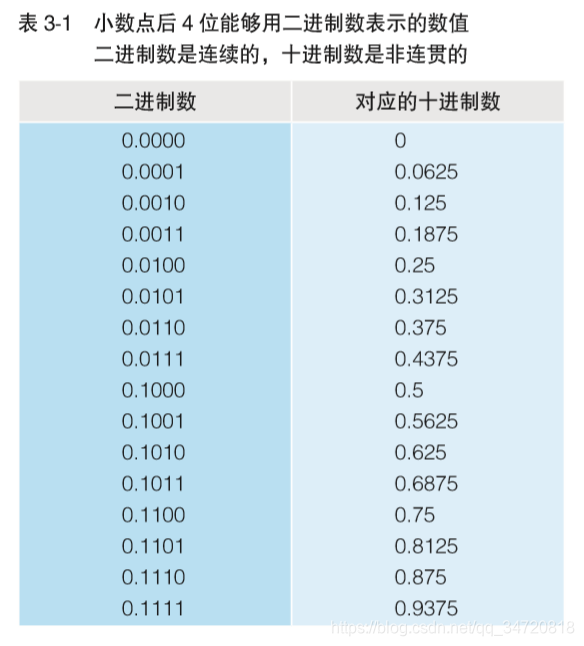
• ，小数点后 4 位用二进制数表示时的数值范围为 0.0000～0.1111。因此，这里只能表示0.5、0.25、0.125、0.0625这四个 二进制数小数点后面的位权组合而成（相加总和）的小数。将这些数值 组合后能够表示的数值，如下表中所示的无序的十进制数。
  

• 由上表可见，十进制数0的下一位是0.0625。因此，这中间的小数， 就无法用小数点后4位数的二进制数来表示。同样，0.0625的下一位 数一下子变成了 0.125。这时，如果增加二进制数小数点后面的位 数，与其相对应的十进制数的个数也会增加，但不管增加多少位， 2 的－○○次幂怎么相加都无法得到0.1这个结果。实际上，十进制数 0.1 转换成二进制后，会变成 0.00011001100…（1100 循环）这样的 循 环小数 A。这和无法用十进制数来表示 1/3 是一样的道理。1/3 就是 0.3333…，同样是循环小数。

三、计算机中表示小数的二进制数是如何存储的呢？

像1011.0011这样带小数点的表现形式，完全是纸面上的二进制数 表现形式，在计算机内部是无法使用的。那么，实际上计算机是以什 么样的表现形式来处理小数的呢？

• 很多编程语言中都提供了两种表示小数的数据类型，分别是双精度浮点数和单精度浮点数。双精度浮点数类型用64位、单精度浮点数类型用32位来表示全体小数。这些数据类型都采用浮点数 B 来表示小数。那么，浮点数究竟采用怎样的方式来表示小数 呢？

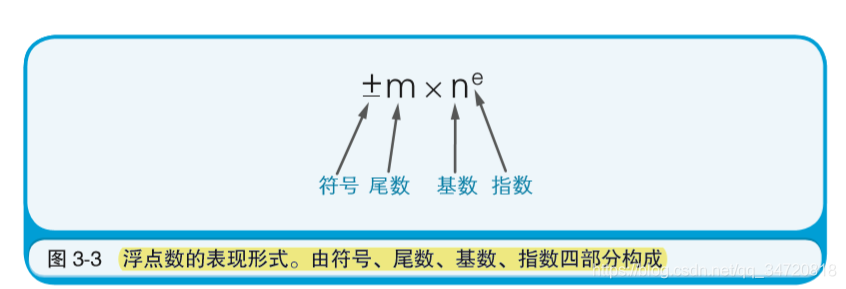
• 浮点数是指用符号、尾数、基数和指数这四部分来表示的小数。
  

• 因为计算机内部使用的是二进制数，所以基数自然就是 2。因 此，实际的数据中往往不考虑基数，只用符号、尾数、指数这三部分 即可表示浮点数。也就是说，64位（双精度浮点数）和32位（单精度 浮点数）的数据，会被分为三部分来使用。
  

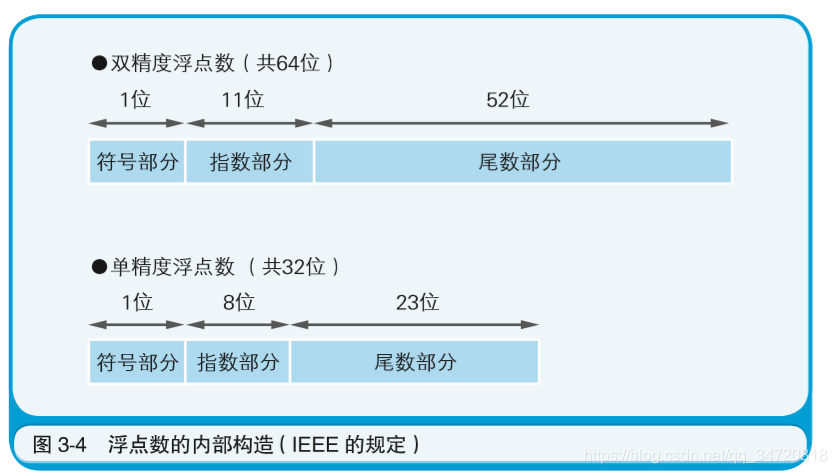
符号部分、指数部分，尾数部分又是如何用二进制表达的呢？

• 符号部分是指使用一个数据位来表示数值的符号。该数据位是1 时表示负，为0时则表示“正或者0”。这和用二进制数来表示整数时 的符号位是同样的。
• 尾数部分用的是“将小数点前面 的值固定为1的正则表达式”
  **什么是正则表达式？**按照特定的规则来表示数据的形式即为正则表达式。是为了将小数的形式统一的一种规则，不然小数的表达形式太多了，计算机如何处理呢？就比如十进制的0.75如果没有规则，就会有无数种表达方式，如
  
  因此，为了方便计算机处理，需要制定一个 统一的规则。例如，十进制数的浮点数应该遵循“小数点前面是0，小 数点后面第 1 位不能是 0”这样的规则。根据这个规则，0.75 就是 “0.75×10 的 0 次幂”，也就是说，只能用尾数部分是 0.75、指数部分 是0这个方法来表示。根据这个规则来表示小数的方式，就是正则表达式。
  同样的道理，二进制表示的小数，如果没有正则表达式（规则），那么也会有无数的形式。因此，我们使用的是“将小数点前面的值固定为1的正则表达 式”，来保证其形式的唯一。具体来讲，就是将二进制数表示的小数左移或右移（这里是逻辑 移位。因为符号位是独立的 B）数次后，整数部分的第1位变为1，第2位之后都变为0（这样是为了消除第2位以上的数位）。而且，第1位的 1在实际的数据中不保存。由于第1位必须是1，因此，省略该部分后就 节省了一个数据位，从而也就可以表示更多的数据范围（虽不算太多）。如二进制数1011.0011的尾数，根据正则表达式要变成如下形式进行保存。
  
• 指数部分用的则是“EXCESS系统表现
  EXCESS 系统表现是指，通过将指数部分表示范围的中间值设为0，使得负数不 需要用符号来表示。也就是说，当指数部分是 8 位单精度浮点数时， 最大值11111111 = 255的1/2，即01111111 = 127（小数部分舍弃）表示 的是0，指数部分是11位双精度浮点数时，11111111111 = 2047的1/2， 即01111111111 = 1023（小数部分舍弃）表示的是0。
  假设有这样一 个游戏，用１～13（A～K）的扑克牌来表示负数。这时，我们可以把中间的 7 这张牌当成 0。如果扑克牌 7 是 0，10 就表示＋3，3 就表 示－4。事实上，这个规则说的就是EXCESS系统。

比如计算机是如何利用浮点数来表示十进制0.75的，我们可以通过代码进行验证

#include<stdio.h>
#include <STRING.H>void main()
{//单精度浮点数计算机中二进制的表示方法（1位表示符号+8位表示指数(正则表达式)+23位表示尾部(EXCESS系统法)）float data; unsigned long buff;int i;char s[34];// 将 0.75 以单精度浮点数的形式存储在变量 date 中data=(float)0.75;// 把数据复制到 4 字节长度的整数变量 buff 中以逐个提取出每一位memcpy(&buff,&data,4);// 逐一提取出每一位for (i = 33; i >= 0; i--) {// 加入破折号来区分符号部分、指数部分和尾数部分if (i==1||i==10){s[i] = '-';}else{// 为各个字节赋值 '0' 或者 '1'if (buff % 2 == 1){s[i]='1';}else{s[i]='0';}buff/=2;}}s[34]='\0';printf("%s\n",s);
}

运行结果如下

这里，符号部分为0，指数部分为 01111110，尾数部分为 10000000000000000000000。因为 0.75 是 正数，所以符号位是 0。指数部分的 01111110 是十进制数 126，用 EXCESS系统表现就是－ 1（126－ 127 = － 1）。根据正则表达式的规则， 小数点前面的第1位是1，因此尾数部分10000000000000000000000实 际上表示的是1.10000000000000000000000这个二进制数。将尾数部分 的二进制数转换成十进制数，结果就是（1 × 2的0次幂）＋（1 × 2的－1次幂） = 1.5。因此，0-01111110-10000000000000000000000这个单精度 浮点数，表示的就是“+ 1.5 × 2的－1次幂”。2的－1次幂是0.5，+ 1.5 × 0.5 = + 0.75。正好吻合，结果正确。

如何避免计算机计算出错？

有两种方法：
第一、回避策略，即无视这些错误。
第二、把小数转换成整数来计算。例如，将0.1相加 100 次这一计算，就可以转换为将 0.1 扩大 10 倍后再将 1 相加 100 次的计算，最后把结果除以10就可以了。