一晃工作有段时间了，第一次写博客，有点不知道怎么写，大家将就着看吧，说的有什么不正确的也请大家指正。

最近工作中用到了一个图像压缩的功能。找了一些工具，没有太好的选择。最后选了一个叫jdeli的，奈何效率又成了问题。我迫于无奈就只能研究了下它的源码，却发现自己对它的一个减色量化算法起了兴趣，可是尴尬的自己完全不明白它写的什么，就起了一个自己实现一个量化颜色算法的念头。

自己找了一些资料，找到三个比较常用的颜色处理算法：

流行色算法：

具体的算法就是，先对一个图像的所有颜色出现的次数进行统计，选举出出现次数最多的256个颜色作为图片的调色板的颜色，然后再次遍历图片的所有像素，对每个像素找出调色板中的最接近的颜色(这里我用的是方差的方式)，写回到图片中。这个算法的实现比较简单，但是失真比较严重，图像中一些出现频率较低，但对人眼的视觉效挺明显的信息将丢失。比如，图像中存在的高亮度斑点，由于出现的次数少，很可能不能被算法选中，将被丢失。

中位切分算法：

这个算法我没有研究，想要了解的同学，可以看下,里面有三种算法的介绍。

八叉树

这个算法就是我最后选用的算法，它的主要思想就是把图像的rgb颜色值转成二进制分布到八叉树中，例如：(173,234,144)

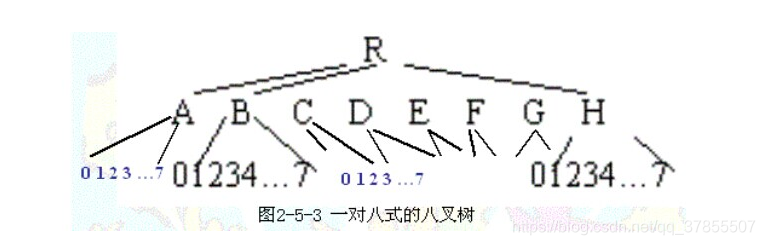
转成二进制就是(10101101,11101010,10010000)，将r,g,b的第一位取出来组成(111)，作为root节点的子节点，其中111作为root子节点数组的索引，以此类推，一直到最后一位，然后在叶子节点上存放这个颜色的分量值以及其出现的次数。具体看图。

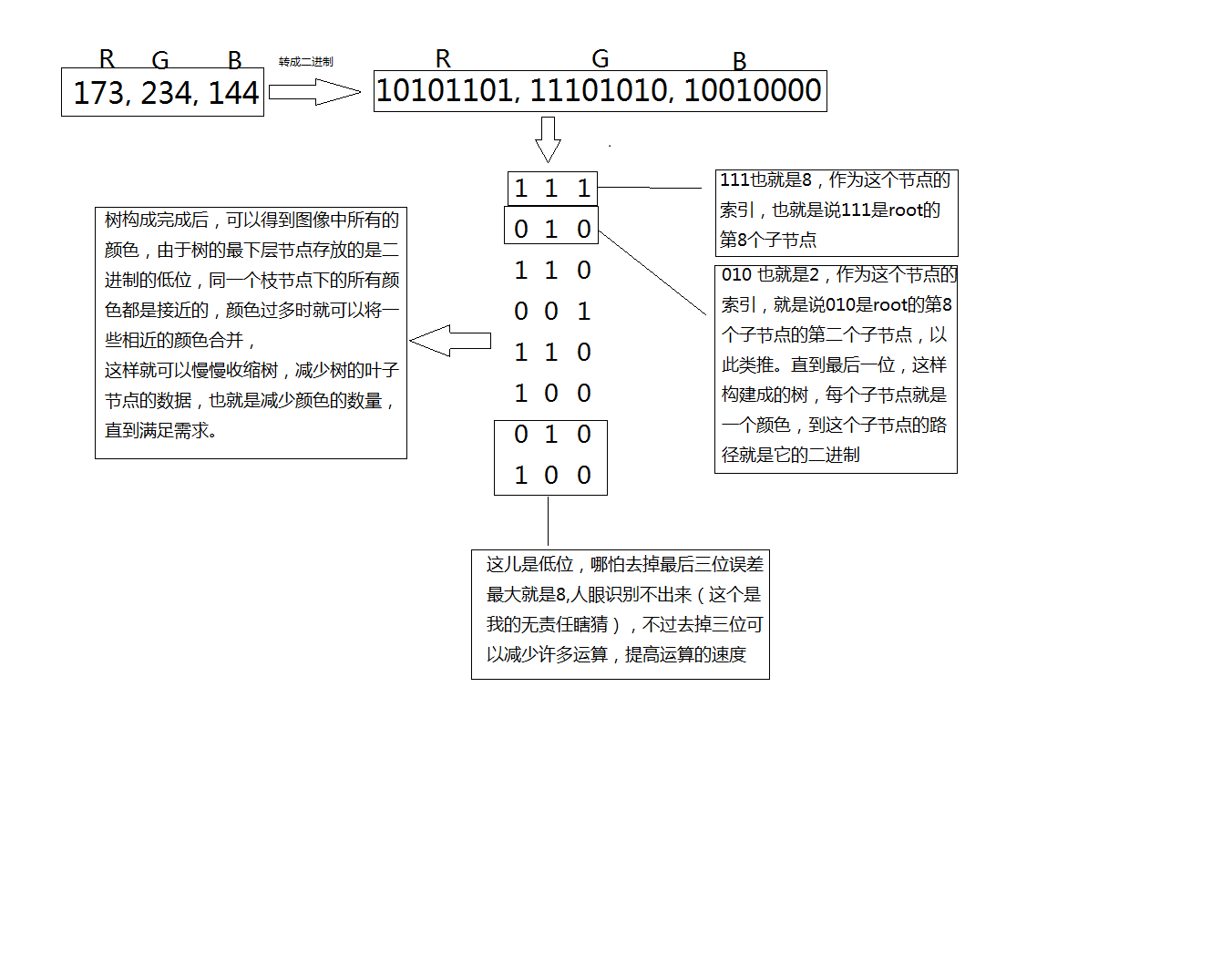
其中我比较疑惑的有一个处理就是叶子节点的合并策略，这儿我用的最笨的一个方法，就是找到层次最深的节点，然后合并，有点简单粗暴，有别的比较好的方法，也请大家给我留言。图片太大上传不了了，直接上代码了，代码没有重构，大家凑合看吧。

package com.gys.pngquant.octree;

import java.util.arraylist;

import java.util.hashmap;

import java.util.list;

import java.util.map;

/**

*

*

* @classname 类名：node

* @description 功能说明：

*

* 八叉树实现

*

*

* 2015-12-16 guoys 创建该类功能。

*

**********************************************************

*

*/

public class node{

private int depth = 0;

// 为0时为root节点

private node parent;

private node[] children = new node[8];

private boolean isleaf = false;

private int rnum = 0;

private int gnum = 0;

private int bnum = 0;

private int piexls = 0;

private map> levelmapping;

// 存放层次和node的关系

public int getrgbvalue(){

int r = this.rnum / this.piexls;

int g = this.gnum / this.piexls;

int b = this.bnum / this.piexls;

return (r << 16 | g << 8 | b);

}

public map> getlevelmapping() {

return levelmapping;

}

public void aftersetparam(){

if(this.getparent() == null && this.depth == 0){

levelmapping = new hashmap>();

for (int i = 1; i <= 8; i++) {

levelmapping.put(i, new arraylist());

}

}

}

public int getrnum() {

return rnum;

}

public void setrnum(int rnum) {

if(!isleaf){

throw new unsupportedoperationexception();

}

this.rnum = rnum;

}

public int getgnum() {

return gnum;

}

public void setgnum(int gnum) {

if(!isleaf){

throw new unsupportedoperationexception();

}

this.gnum = gnum;

}

public int getbnum() {

return bnum;

}

public void setbnum(int bnum) {

if(!isleaf){

throw new unsupportedoperationexception();

}

this.bnum = bnum;

}

public int getpiexls() {

return piexls;

}

public void setpiexls(int piexls) {

if(!isleaf){

throw new unsupportedoperationexception();

}

this.piexls = piexls;

}

public int getdepth() {

return depth;

}

// 返回节点原有的子节点数量

public int mergerleafnode(){

if(this.isleaf){

return 1;

}

this.setleaf(true);

int rnum = 0;

int gnum = 0;

int bnum = 0;

int pixel = 0;

int i = 0;

for (node child : this.children) {

if(child == null){

continue;

}

rnum += child.getrnum();

gnum += child.getgnum();

bnum += child.getbnum();

pixel += child.getpiexls();

i += 1;

}

this.setrnum(rnum);

this.setgnum(gnum);

this.setbnum(bnum);

this.setpiexls(pixel);

this.children = null;

return i;

}

// 获取最深层次的node

public node getdepestnode(){

for (int i = 7; i > 0; i--) {

list levellist = this.levelmapping.get(i);

if(!levellist.isempty()){

return levellist.remove(levellist.size() - 1);

}

}

return null;

}

// 获取叶子节点的数量

public int getleafnum(){

if(isleaf){

return 1;

}

int i = 0;

for (node child : this.children) {

if(child != null){

i += child.getleafnum();

}

}

return i;

}

public void setdepth(int depth) {

this.depth = depth;

}

public node getparent() {

return parent;

}

public void setparent(node parent) {

this.parent = parent;

}

public node[] getchildren() {

return children;

}

public node getchild(int index){

return children[index];

}

public void setchild(int index, node node){

children[index] = node;

}

public boolean isleaf() {

return isleaf;

}

public void setpixel(int r, int g, int b){

this.rnum += r;

this.gnum += g;

this.bnum += b;

this.piexls += 1;

}

public void setleaf(boolean isleaf) {

this.isleaf = isleaf;

}

public void add8bite2root(int _taget, int _speed){

if(depth != 0 || this.parent != null){

throw new unsupportedoperationexception();

}

int speed = 7 + 1 - _speed;

int r = _taget >> 16 & 0xff;

int g = _taget >> 8 & 0xff;

int b = _taget & 0xff;

node pronode = this;

for (int i=7;i>=speed;i--){

int item = ((r >> i & 1) << 2) + ((g >> i & 1) << 1) + (b >> i & 1);

node child = pronode.getchild(item);

if(child == null){

child = new node();

child.setdepth(8-i);

child.setparent(pronode);

child.aftersetparam();

this.levelmapping.get(child.getdepth()).add(child);

pronode.setchild(item, child);

}

if(i == speed){

child.setleaf(true);

}

if(child.isleaf()){

child.setpixel(r, g, b);

break;

}

pronode = child;

}

}

public static node build(int[][] matrix, int speed){

node root = new node();

root.aftersetparam();

for (int[] row : matrix) {

for (int cell : row) {

root.add8bite2root(cell, speed);

}

}

return root;

}

public static byte[] mergecolors(node root, int maxcolors){

byte[] bytearray = new byte[maxcolors * 3];

list result = new arraylist();

int leafnum = root.getleafnum();

try{

while(leafnum > maxcolors){

int mergerleafnode = root.getdepestnode().mergerleafnode();

leafnum -= (mergerleafnode - 1);

}

}

catch(exception e){

e.printstacktrace();

}

fillarray(root, result, 0);

int i = 0;

for (byte byte1 : result) {

bytearray[i++] = byte1;

}

return bytearray;

}

private static void fillarray(node node, list result, int offset){

if(node == null){

return;

}

if(node.isleaf()){

result.add((byte) (node.getrnum() / node.getpiexls()));

result.add((byte) (node.getgnum() / node.getpiexls()));

result.add((byte) (node.getbnum() / node.getpiexls()));

} else{

for (node child : node.getchildren()) {

fillarray(child, result, offset);

}

}

}

}

可怜我大学唯二挂的数据结构。代码实现的只是八叉树，对一个1920*1080图片量化，耗时大概是450ms，如果层次-2的话大概是100ms左右。

好吧，这篇就这样吧，本来写之前，感觉自己想说的挺多的，结果写的时候就不知道怎么说了，大家见谅。

总结

以上就是本文关于java简单实现八叉树图像处理代码示例的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站其他相关专题，如有不足之处，欢迎留言指出。感谢朋友们对本站的支持！

希望与广大网友互动？？

点此进行留言吧！