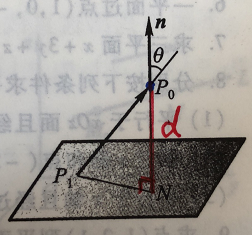
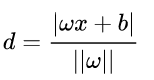1. 法线
一个平面或超平面由一个方程(不是一组方程)定义:
{ x ∣ a T x = b } \{x\mid a^Tx=b\} {x∣aTx=b}
其中 a a a 是一个非零的列向量,而 b b b 是一个实数。那么它的法线(垂线)向量是 a a a。
例如,超平面
2 x + 3 y + 4 z = 5 2x+3y+4z=5 2x+3y+4z=5
它法线向量是: ( 2 , 3 , 4 ) (2, 3, 4) (2,3,4)。它的一个法线是:
x − 1 2 = y − 1 3 = z − 1 4 \frac{x-1}{2}=\frac{y-1}{3}=\frac{z-1}{4} 2x−1=3y−1=4z−1
画图表示:

画图的 matlab 代码:
function DrawHyperPlane
fmesh(@(x,y)1/4*(9-2*x-3*y));
hold on;plot3([-1,3], [-2, 4], [-3, 5]);title('Hyper plane: 2x+3y+4z=9')
str = '$$\frac{x-1}{2}=\frac{y-1}{3}=\frac{z-1}{4}$$';
text(-0.7, 9.8, str, 'Interpreter','latex');
annotation('arrow','X',[0.4,0.5],'Y',[0.6,0.6]end
2. 平行超平面的距离
设一个超平面为 a T x = b 1 a^Tx=b_1 aTx=b1,另一个超平面为 a T x = b 2 a^Tx=b_2 aTx=b2,求两个超平面的距离。
解: 超平面的法线向量为 a a a,经过第一个超平面上的点 x 1 x_1 x1 的法线为: x = x 1 + t a x=x_1+ta x=x1+ta, ( t ∈ R ) (t\in R) (t∈R)。则该法线与第二个超平面的交点满足:
a T ( x 1 + t a ) = b 2 a^T(x_1+ta)=b_2 aT(x1+ta)=b2
因此 t = ( b 2 − a T x 1 ) / a T a t=(b_2-a^Tx_1)/a^Ta t=(b2−aTx1)/aTa, 因此
x 2 = x 1 + ( b 2 − a T x 1 ) a a T a = x 1 + ( b 2 − b 1 ) a a T a x_2=x_1+\frac{(b_2-a^Tx_1)a}{a^Ta}=x_1+\frac{(b_2-b_1)a}{a^Ta} x2=x1+aTa(b2−aTx1)a=x1+aTa(b2−b1)a
连个超平面的距离即为 x 1 x_1 x1 与 x 2 x_2 x2 的距离:
∥ x 2 − x 1 ∥ = ∥ ( b 2 − b 1 ) a a T a ∥ = ∣ b 2 − b 1 ∣ ∥ a ∥ \|x_2-x_1\|=\|\frac{(b_2-b_1)a}{a^Ta}\|=\frac{|b_2-b_1|}{\|a\|} ∥x2−x1∥=∥aTa(b2−b1)a∥=∥a∥∣b2−b1∣
如下图所示: