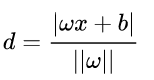背景

• 关于超平面的介绍，网上的博客资料太多了，然而真正简洁易懂、切中要害的实在是太少了，我在学习这个问题的过程中遇到了太多坎坷，这里将一些比较直白易懂的讲解和个人理解展示出来。
• 引用的一些图片、公式等来源于：https://www.cnblogs.com/yanghh/p/13617129.html

定义

• 见下图
  
  我不太想在定义上就用一些很复杂的解释手法，有很多博客在定义上就很吓唬人，很影响阅读体验，所以我觉得没必要在定义上引用一些很深奥的知识，而是力求让读者能够在心里直观地明白，嗷，这么个东西就是超平面。

超平面方程推导

• 我们从平面直线方程到空间平面方程，最后推广到超平面。

平面直线方程

• 见下图：
  
  
  这个思路非常好，直线其实就是一个常向量和另一个变化的向量的内积为定值 c。 这里的常向量就是直线的法向量，也就是说，给你一个法向量了，此时直线还不是确定的，直线可以沿着法向量平移，然后再给你一个定值c，就完权固定了这条直线，因为法向量和(x,y）内积为c的直线只有一条。
  另外一定要注意这句话，
  
  比如2x+3y+2=0，表示一个平面，两边同乘2得，4x+6y+4=0依然表示的是同一个平面，然而c和w都变成了原来的两倍，与原来的意义不同了。而且我记得在高中的时候所说的法向量就是求到最简的时候的法向量。
  另外还要注意的是向量内积的含义，
  
  内积是一个实数哦，当你的角度确定了，两个向量的模确定了，内积就确定了，内积通过角度可以用来衡量两个向量的方向的接近程度，
  
  这样我们再最后梳理一下，
  
  不管(x,y)取何值，它和法向量的内积都是一个定值c，为什么呢？因为不管(x,y)取何值，|b|cosθ（θ是法向量和它的夹角）都是一个定值，而|a|（即|法向量|）也是一个定值，所以内积为定值c。

空间平面方程

• 下面推广到空间平面方程
  

超平面

• 下面推广到超平面
  

点到超平面的距离推导

• 我们从点到直线的距离出发，再到点到平面的距离，最后推广到超平面

点到平面直线的距离

• 有以下距离公式：
  
  具体推导过程好像高中还是初中应该有，这里提供一种推导过程（可跳过）：
  
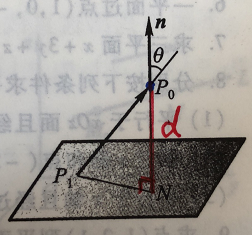
• 然后我们看到下面的示意图：
  
  这一步所以后面的公式我没弄明白是为啥，继续往下看：
  

点到空间平面的距离

• 推广到点到空间平面的距离：
  

超平面

• 引申到超平面
  

判断超平面的正反

• 继续