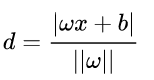王二麻听说躺平国是一个非常神奇的地方。在躺平国里,有各种神奇的东西。比如:会说话的铁片,能够分拣垃圾的小狗,还有会唱京剧的电线杆子。
王二麻的表哥张三李是一个糙汉子,他前几年在国内混不下去了,一个人去了躺平国。那是一个快乐的国度,每一个人都可以躺平,或者做自己热爱的事情。
他们可以把日常的事物交给特点的躺平机处理。
王二麻也想去躺平国,但是在去躺平国的路上需要经历许许多多的困难。 他非常的畏惧。
于是,张三李一直写信给王二麻,教张三李怎么样度过他路途中需要解决的困难,也会给王二麻讲躺平国的奇闻异事。
- 白沙天堑
张三李在给王二麻写的第一封信里面,讲了王二麻会遇到的第一个关卡: 白沙天堑。
白沙天堑是一个大峡谷,上面没有可以通行的桥梁。白沙天堑下面是白色河,白沙和里面白色的河沙是没有能够度过天堑的挑战者的白骨的细屑,所有没能通过白沙天堑的挑战者被躺平国称为——“小白沙雕”。
白沙天堑崖壁是平行的,这两个崖壁之间的距离会随机变化,但是崖壁旁边的石台上会展示两个崖壁上所有点满足的公式,并且提供一个可以跳跃宽度为 d d d 的 白沙靴。
为了能够安全的度过白沙天堑,挑战者必须能够计算出天堑的两个崖壁之间的距离。当崖壁之间的距离能够小于等于 白沙靴 的跳跃距离的时候,王二麻就可以拿出靴子跳过天堑。
1 崖壁的表示
为了更简单的描述问题,我们将两个崖壁描述为两个平行的超平面。
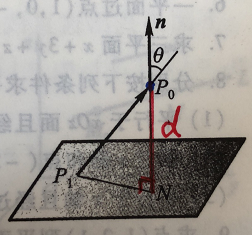
 图 1 点到平面的距离
图 1 点到平面的距离
如上图1所示,为一个超平面 L 1 L_1 L1, 对超平面上的每一个点 x = ( d 1 , d 2 , . . . , d n ) ∈ R n x=(d_1,d_2,...,d_n) \in R^n x=(d1,d2,...,dn)∈Rn 满足如下条件:
w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
其中, w w w 为超平面 L 1 L_1 L1 的法向量。
2 天堑距离的计算
假设,白沙天堑对应的两个崖壁表示的超平面分别为 L s L_s Ls L e L_e Le, 其中 L s L_s Ls表示起跳超平面, L e L_e Le表示落地超平面。王二麻的目的就是为了从, L s L_s Ls 跳到 L e L_e Le 那么我们需要计算两个超平面之间的距离 d d d 来判断跳跃是否成功。
首先,假设王二麻站定点的坐标为 S S S, 在超平面 L e L_e Le 上离他最近的落地点的坐标为 E E E。
设 L s L_s Ls 满足公式:
w ⋅ x + b 1 = 0 w \cdot x + b_1 = 0 w⋅x+b1=0
L e L_e Le 满足公式:
w ⋅ x + b 2 = 0 w \cdot x + b_2 = 0 w⋅x+b2=0
那么:
d = ∣ S E → ∣ d = |\overrightarrow{SE}| d=∣SE∣
并且 S E → \overrightarrow{SE} SE 与平面的法向量平行。
∣ w ⋅ S E → ∣ = ∣ w ∣ ∣ S E → ∣ = w 1 2 + w 2 2 + . . . + w n 2 d = ∣ ∣ w ∣ ∣ d ( 1 ) | w \cdot \overrightarrow {SE} | = |w| |\overrightarrow {SE}| = \sqrt {w_1^2 + w_2^2 + ... + w_n^2} d = ||w||d \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (1) ∣w⋅SE∣=∣w∣∣SE∣=w12+w22+...+wn2d=∣∣w∣∣d(1)
并且
∣ w ⋅ S E → ∣ = ∣ w 0 ( S 0 − E 0 ) + w 1 ( S 1 − E 1 ) + . . . + w n ( S n − E n ) ∣ = ∣ ( w 0 S 0 + w 1 S 1 + . . . + w n S n + b 1 ) − ( w 0 E 0 + w 1 E 1 + . . . + w n E n + b 2 ) − b 1 + b 2 ∣ = ∣ − b 1 + b 2 ∣ ( 2 ) | w \cdot \overrightarrow {SE} | = |w_0 (S_0-E_0) + w_1 (S_1-E_1) + ... + w_n(S_n-E_n)| \\ = |(w_0 S_0+ w_1S_1 + ... + w_n S_n + b_1) - (w_0 E_0+ w_1E_1 + ... + w_n E_n + b_2) - b1 + b2| \\ = |-b1 + b2| \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (2) ∣w⋅SE∣=∣w0(S0−E0)+w1(S1−E1)+...+wn(Sn−En)∣=∣(w0S0+w1S1+...+wnSn+b1)−(w0E0+w1E1+...+wnEn+b2)−b1+b2∣=∣−b1+b2∣(2)
根据公式(1)和(2) 得到:
∣ ∣ w ∣ ∣ d = ∣ − b 1 + b 2 ∣ ||w||d = |-b1 + b2| ∣∣w∣∣d=∣−b1+b2∣
那么两个平面的距离 d = ∣ − b 1 + b 2 ∣ ∣ ∣ W ∣ ∣ d = \frac{|-b1 + b2|}{||W||} d=∣∣W∣∣∣−b1+b2∣