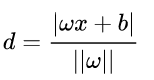（1）超平面方程

3维空间中平面方程的一般形式：

   (1)

我们都知道为平面到原点的距离。这里简单证明超平面的法向量为。

d维空间平面方程的一般形式：

    (2)

平面的法向量为，（分号表示列向量）。

（2）向量表示

3维空间中的向量可以用点坐标来表示。向量表示一个过原点与该点的向量。

两个向量和垂直的充要条件为：

  (3)

即，

  (4)

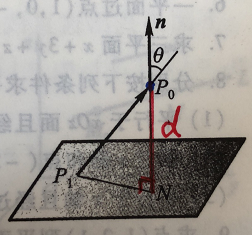
（3）超平面的法向量

为什么超平面的法向量为？

以3维空间为例，设平面上任意两点,，由于两个点都在平面上，所以均满足平面方程：

 上两式相减得：

  (5)

连线构成的向量为

由式(5)可知，向量。

由于,是平面上任意两点，所以为平面上任意一条直线。

所以，向量与三维平面(1)上任意一条直线垂直，它就是平面(1)的法向量。

同理，扩展到d维空间超平面(2)的法向量为：。