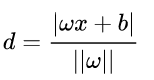如何理解超平面？

article/2025/9/17 6:06:11

超平面的公式

首先明确几个定义：(1) 超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中，一条直线是一维的，它把平面分成了两块；三维空间中，一个平面是二维的，它把空间分成了两块。(2) 法向量是指垂直于超平面的向量。

在 $R^{3}$ 空间中，假如有法向量 $\large \omega$ ，过原点的平面内任意原点出发的向量 x 必然与之满足

$\large \omega ^{T}\ \cdot x = 0$

。如果平面沿着法向量的方向上下平移了，那么这个方程就不成立了。

我们假设平移之后平面经过 $\large x^{'}(x_{1}^{'},x_{2}^{'},x_{3}^{'})$ ，平面内任意一点记为 $\large x(x_{1},x_{2},x_{3})$ ，法向量记为 $\large \omega (\omega _{1},\omega _{2},\omega _{3})$ ，如下图。

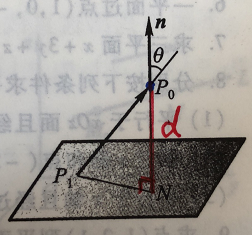
平面公式示意图

不难看出， $\large x-x^{'}$ 在平面内，当然也就和法向量垂直。于是我们有：

$\large (x-x^{'})\omega = 0$

$\large (x_{1}-x_{1}^{'},x_{2}-x_{2}^{'},x_{3}-x_{3}^{'})\cdot (\omega _{1},\omega _{2},\omega _{3})) = 0$
化简后得：

$\large x_{1}\omega _{1} + x_{2}\omega _{2} + x_{3}\omega _{3} = x_{1}^{'}\omega _{1} + x_{2}^{'}\omega _{2} + x_{3}^{'}\omega _{3}$ 。

即

$\large \omega ^{T}x = \omega ^{T}x^{'}$

。由于其为常数项，令

$\large b = -\omega ^{T}x^{'}$

，于是超平面的公式可以写成：

$\large \omega ^{T}x + b = 0$

这个结论同样适用于 $\large R^{n}$ 空间；

无论超平面如何平移，系数始终是法向量 $\large \omega$ 。

点到超平面的距离

点到超平面距离

上图中 $\large x$ 是平面外的一点。我们要求的距离记为 $\large d$ ，也就是红色的线段。根据三角函数可以得到：

$\large cos\theta = \frac{d}{||x-x^{'}||}$

（空间中一点向超平面作垂线， $\large \theta$ 只能是锐角，不必担心正负）。因为 $\large d$ 肯定和法向量平行，所以这样来算夹角：

$\large |(x-x^{'})\omega | = ||x-x^{'}||\cdot ||\omega ||cos\theta$

（因为法向量可能反向，所以给等式左边加上绝对值），联立得：

$\large d = \frac{|(x-x^{'})\omega |}{||\omega ||} = \frac{|\omega x - \omega x^{'}|}{||\omega ||}$
因为 $\large x^{'}$ 在超平面内， $\large \omega x^{'} = -b$ ，于是最后得到的任意点到超平面的距离公式：