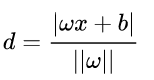前言
定义:
1、超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。比如二维空间中,一条直线是一维的,它把平面分成了两块;三维空间中,一个平面是二维的,它把空间分成了两块。
2、法向量是指垂直于超平面的向量。
过原点的超平面
假设在R3空间中,有一个过原点的超平面,其法向量为 ω ⃗ \vec{\omega} ω( ω \omega ω1, ω \omega ω2, ω \omega ω3),过原点的平面内任意原点出发的向量 x ⃗ \vec{x} x,必有 ω \omega ωTx = 0。
故超平面公式为: ω \omega ωTx = 0
非过原点的超平面

假设在R3空间中,有一个经过原点的超平面上下平移后的超平面,其法向量为 ω ⃗ \vec{\omega} ω( ω \omega ω1, ω \omega ω2, ω \omega ω3),此时 ω \omega ωTx = 0就不成立了。令超平面上有两点,它与原点分别组成向量x(x1,x2,x3)和向量x ′ \prime ′(x ′ \prime ′1,x ′ \prime ′2,x ′ \prime ′3),不难看出平面上两点组成的向量必与法向量垂直。可得:
( x − x ′ ) ω = ( x 1 − x ′ 1 , x 2 − x ′ 2 , x 2 − x ′ 3 ) ( ω 1 , ω 2 , ω 3 ) = 0 (x-x\prime) \omega = (x_1- x\prime_1,x_2- x\prime_2,x_2- x\prime_3)(\omega_1,\omega_2,\omega_3)= 0 (x−x′)ω=(x1−x′1,x2−x′2,x2−x′3)(ω1,ω2,ω3)=0
化简后可得:
x 1 ∗ ω 1 + x 2 ∗ ω 2 + x 3 ∗ ω 3 = x ′ 1 ∗ ω 1 + x ′ 2 ∗ ω 2 + x ′ 3 ∗ ω 3 x_1*\omega_1 + x_2*\omega_2+ x_3*\omega_3 = x\prime_1*\omega_1 + x\prime_2*\omega_2+ x\prime_3*\omega_3 x1∗ω1+x2∗ω2+x3∗ω3=x′1∗ω1+x′2∗ω2+x′3∗ω3
ω T x = ω T x ′ \omega^Tx = \omega^Tx\prime ωTx=ωTx′
令 b = ω \omega ωT x ′ \prime ′,则可得
ω T x + b = 0 \omega^Tx + b = 0 ωTx+b=0
即最后超平面方程是 ω \omega ωTx + b = 0
点到超平面的距离
假设平面外一点x到超平面距离为d,即上图的红线长度。上图的 θ \theta θ是向量xx ′ \prime ′和红线距离的夹角。故可得:
cos θ = d ∣ ∣ x − x ′ ∣ ∣ \cos \theta = \frac{ d }{ || x - x\prime|| } cosθ=∣∣x−x′∣∣d
又因为红线和超平面法线平行,故向量xx ′ \prime ′和法线夹角也为 θ \theta θ。故|(x - x ′ \prime ′)* ω \omega ω| = || ω \omega ω|| * ||(x - x ′ \prime ′)|| * cos \cos cos θ \theta θ,联立两个方程,可得
d = ∣ ( x − x ′ ) ω ∣ ∣ ∣ ω ∣ ∣ = ∣ ω x − ω x ′ ∣ ∣ ∣ ω ∣ ∣ = ∣ ω x + b ∣ ∣ ∣ ω ∣ ∣ d = \frac{ |(x-x \prime) \omega| }{ || \omega|| } = \frac{ | \omega x- \omega x \prime | }{ || \omega|| } = \frac{ | \omega x+b| }{ || \omega|| } d=∣∣ω∣∣∣(x−x′)ω∣=∣∣ω∣∣∣ωx−ωx′∣=∣∣ω∣∣∣ωx+b∣