模拟退火

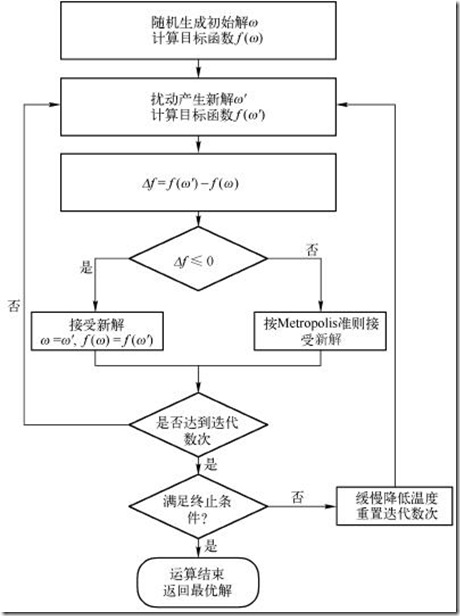
模拟退火($SimulatedAnnealing[SA]$)的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。

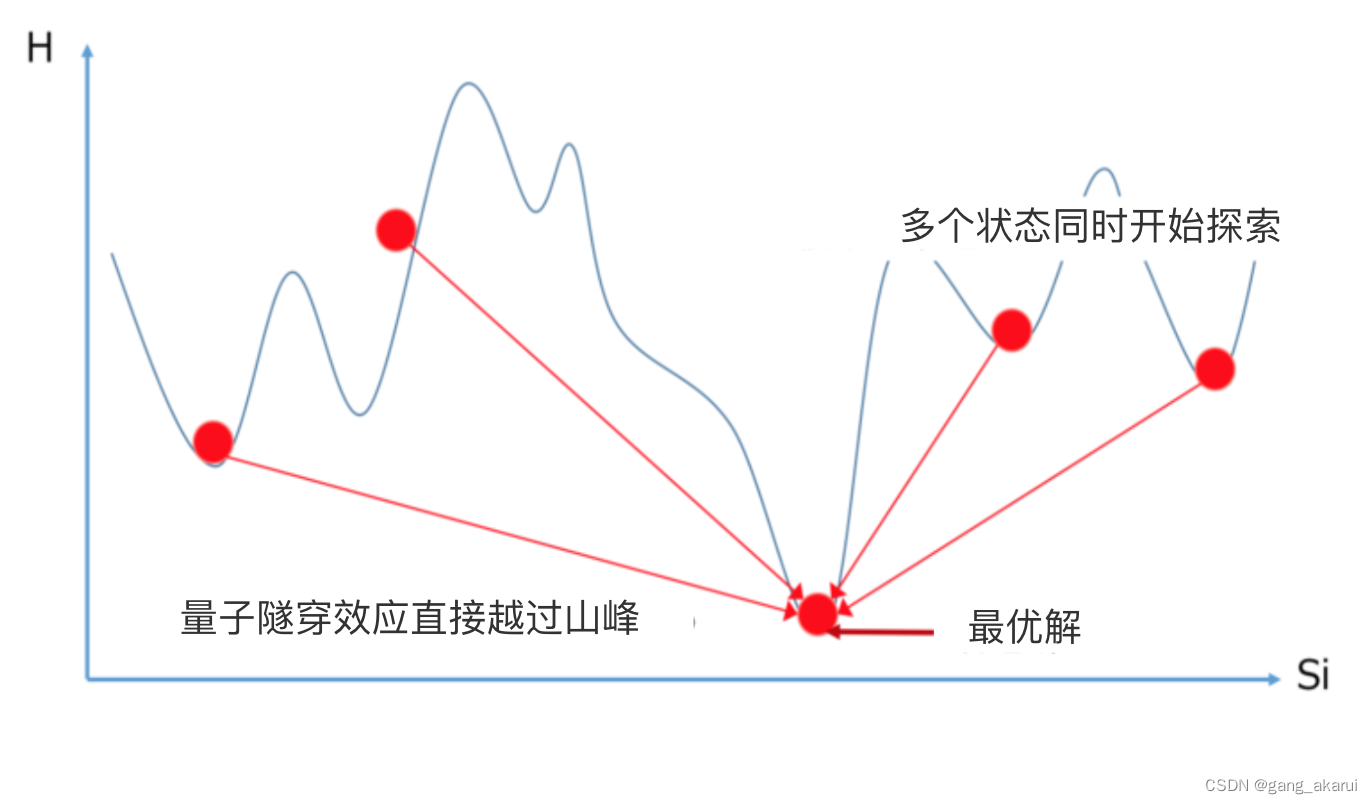
模拟退火算法是基于$Monte-Carlo$迭代求解策略的一种随机寻优算法，从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。

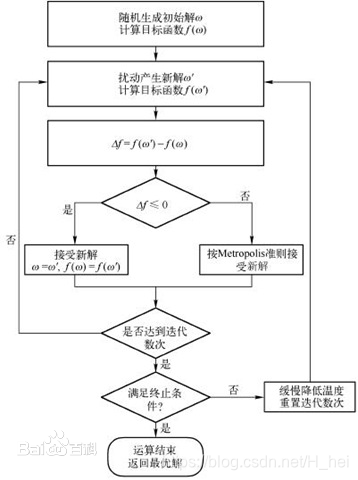
算法流程

每次随机出一个新解，设当前温度为$t$、新解对应的函数值与当前最优解的差为$\Delta E$。如果这个解更优即$\Delta E<0$则接受它为当前最优解；否则以一定的概率$e^{\frac{\Delta E}{t}}$接受它为当前可能最优解，即随机出的概率小于$e^{\frac{\Delta E}{t}}$。

算法伪代码：

Status SA() {t = 初始温度;delta = 降温参数;eps = 最终停止的阈值;ans = 答案, tmp = 可能最优状态;while(t > eps) {nxt = 从当前找到的可能最优状态随机找到的一个状态;del = f(nxt) - f(ans);if (del < 0) {ans = tmp = ans;  //更新最优解和可能最优解}else if (exp(-del / t) * RAND_MAX > rand()) {  //实际上是rand()*1.0 / RAND_MAX，这里是减少浮点数计算误差tmp = nxt;   //以一定概率取得非最优解然后保存尝试}t *= delta;}return ans;
}

如何得到尽可能精确的解

• 随机数种子设置：可以先设置一个大质数，然后随机几次随机数种子，如$srand(100000007),srand(rand())$，注意不能$srand(time(0))$。

• 初始最优解：一般取给出所有初始状态的一个平均值状态，更易得到最优解。

• 初始温度$T$的设置：大部分题目设置为$100$都可以过，但是有的范围比较大，一般不超过这个范围的初始温度都可以尝试，自行调整。

• 温度停止阈值$eps$的设置，一般设置到$1e^{-10}$左右即可，如果不行就设置到$1e^{-14}$（前提不超时），自行调整。

• 降温参数$delta$的设置：一般来说降温参数取$[0.93,0.99]$即可，如果不行就调整到$[0.993,0.999]$（前提不超时），自行调整。

• 在不超时的前提下多跑几遍模拟退火，即在前面跑出最优解的基础上再去跑模拟退火。

时间复杂度

时间复杂度和上述的三个影响解的参数$T,eps,delta$息息相关，因此得出结论：玄学复杂度。

应用一：求函数的最值

HDU-2899

现在有方程$f(x)=6\ast x^7+8\ast x^6+7\ast x^3+5\ast x^2-k\ast x(0\le x\le 100)$，每次给出$k$，求该函数在$[0,100]$的最小值。

代码

需要注意的是，因为本题有定义域的限制，我们在随机寻找最优解的时候应该限制在定义域中。

const double T = 100;
const double delta = 0.996;
const double eps = 1e-14;
double y;double f(double x) {return 6.0 * pow(x, 7.0) + 8.0 * pow(x, 6.0) + 7.0 * pow(x, 3.0) + 5.0 * pow(x, 2.0) - y * x;
}double SA() {double t = T, ans = 50;double tmp = ans;while (t > eps) {double nxt = tmp + (rand() * 2.0 - RAND_MAX) * t;while (nxt < 0) nxt = tmp + (rand() * 2.0 - RAND_MAX) * t;double del = f(nxt) - f(ans);if (del < 0) {ans = tmp = nxt;} else if (exp(-del / t) * RAND_MAX > rand()) {tmp = nxt;}t *= delta;}return ans;
}void solve() {int T;scanf("%d", &T);while (T--) {srand(100000007);srand(rand()), srand(rand());scanf("%lf", &y);printf("%.4lf\n", f(SA()));}
}

应用二：求费马点

POJ-2420

给出平面内的$n$个点找出费马点，即找到一个点使得该点到其他所有点的距离之和最小，输出这个最小距离。

代码

const double eps = 1e-14;
const double dinf = 1e300;
const double delta = 0.993;
const double T = 100;struct Point {double x, y;Point(double a = 0, double b = 0) : x(a), y(b) {}
} p[105];int n;
Point s;double dis(Point a, Point b) {return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}double f(Point cur) {double ans = 0;for (int i = 0; i < n; i++) {ans += dis(cur, p[i]);}return ans;
}double SA() {double t = T, ans = dinf;Point tmp = s;while (t > eps) {Point nxt(tmp.x + (rand() * 2.0 - RAND_MAX) * t, tmp.y + (rand() * 2.0 - RAND_MAX) * t);double res = f(nxt);double del = res - ans;if (del < 0) {ans = res;s = tmp = nxt;} else if (exp((ans - res) / t) * RAND_MAX > rand()) {tmp = nxt;}t *= delta;}return ans;
}void solve() {srand(100000007);srand(rand()), srand(rand());scanf("%d", &n);double sumx = 0, sumy = 0;for (int i = 0; i < n; i++) {scanf("%lf%lf", &p[i].x, &p[i].y);sumx += p[i].x, sumy += p[i].y;}s = Point(sumx / n, sumy / n);printf("%.0lf\n", SA());
}

应用三：求最小球覆盖

Gym101981D - Country Meow

给出三维坐标系的若干个点，在坐标系范围内找到一个点作为圆心，在给出的点中距离它最远的点的距离作为半径作出一个球，该球内包含了其余所有的给定点。

代码

const double T = 100000;
const double delta = 0.998;
const double eps = 1e-14;
const double dinf = 1e300;struct Point {double x, y, z;Point(double a = 0, double b = 0, double c = 0) : x(a), y(b), z(c) {}
} p[105];int n;
Point s;double dis(Point a, Point b) {return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z));
}int f(Point cur) {int ans = 0;for (int i = 1; i < n; i++) {if (dis(cur, p[i]) > dis(cur, p[ans])) {ans = i;}}return ans;
}double SA() {double t = T, ans = dinf;Point tmp = s, nxt;while (t > eps) {nxt.x = tmp.x + (rand() * 2 - RAND_MAX) * t;nxt.y = tmp.y + (rand() * 2 - RAND_MAX) * t;nxt.z = tmp.z + (rand() * 2 - RAND_MAX) * t;int k = f(nxt);double res = dis(nxt, p[k]);double del = res - ans;if (del < 0) {ans = res;s = tmp = nxt;} else if (exp(-del / t) * RAND_MAX > rand()) {tmp = nxt;}t *= delta;}return ans;
}void solve() {srand(23333333);srand(rand()), srand(rand());scanf("%d", &n);double sumx = 0, sumy = 0, sumz = 0;for (int i = 0; i < n; i++) {scanf("%lf%lf%lf", &p[i].x, &p[i].y, &p[i].z);sumx += p[i].x, sumy += p[i].y, sumz += p[i].z;}s = Point(sumx / n, sumy / n, sumz / n);printf("%.8lf\n", SA());
}