本博客封面由
ChatGPT + DALL·E 2共同创作而成。
文章目录
- 前言
- 1. 算法思想
- 2. 细节梳理
- 2.1 超参数的选择
- 2.2 一些trick
- 3. 算法实现
- 3.1 问题场景
- 3.2 从算法角度分析
- 3.3 python实现
- 代码仓库:IALib[GitHub]
前言
本篇是智能算法(Python复现)专栏的第二篇文章,主要介绍模拟退火算法(Simulate Anneal Algorithm, SAA)的思想,python实现及相关应用场景模拟。
模拟退火算法,顾名思义,就是对固体退火这一热力学过程的模拟,它是一种适合解决大规模组合优化问题的随机搜索算法。与一般的局部搜索算法不同的是,SAA以一定的概率选择邻域中目标值相对较小的状态,从理论上来说,它是一种全局最优算法。
1. 算法思想
固体退火过程是指将固体加热到熔化,再徐徐冷却使之凝固成规整晶体的热力学过程,主要由加温过程、等温过程以及冷却过程3个阶段组成。
(1) 加温过程:对固体加热时,随着温度的升高,粒子的热运动不断加强,逐渐偏离平衡位置,粒子排列也呈现出随机状态,此时,宏观上物体表现为液态,这就是熔化现象。熔化过程消除了系统内原先可能存在的非均匀状态,同时系统的能量也随着温度升高而增大;
(2) 等温过程:退火过程要求温度缓慢降低,使得系统在每个温度下都达到平衡状态。这一过程可以根据自由能减少定律给出解释:对于与环境发生热量交换而温度保持不变的封闭系统,系统状态的自发变化总是朝着自由能减少的方向进行,当自由能达到最小值时,系统达到平衡态;
(3) 冷却过程:温度的降低使得粒子热运动慢慢减弱,粒子排列渐趋有序,系统能量不断减小,最终得到低能的晶体结构。当液体凝固成固体的晶态时,退火过程完成。
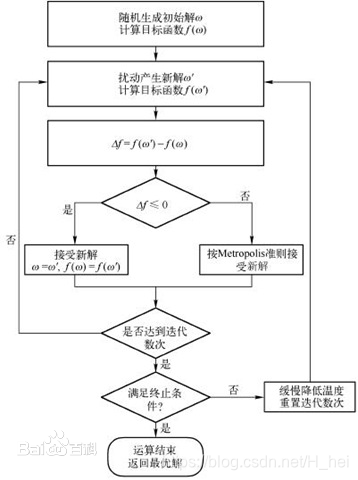
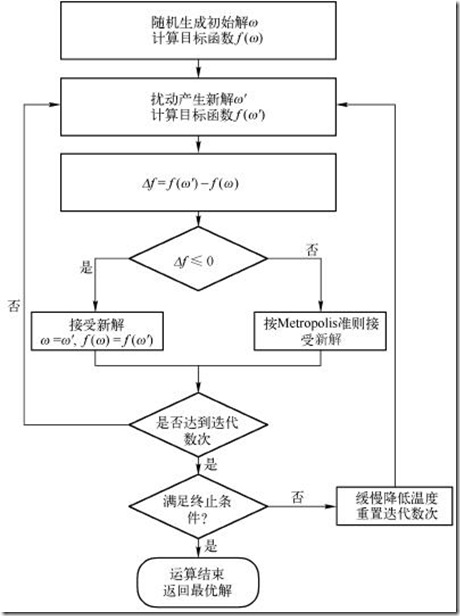
SAA是用来在一个大的搜寻空间内找寻最优解的基于概率的算法,采用类似于固体退火的过程,先将固体加温至充分高(相当于算法的随机搜索),然后徐徐冷却(相当于算法的局部搜索),在每一个温度(相当于算法的每一次状态转移)达到平衡态,最终达到物理基态(相当于算法找到最优解)。
具体可以表述为:粒子在温度 T T T 时趋于平衡的概率为 e x p ( − Δ E k T ) exp(- \frac {\Delta E} {kT}) exp(−kTΔE),其中 E E E 为温度 T T T 时的内能, Δ E ΔE ΔE 为其改变量, k k k 为玻耳兹曼常数。用固体退火模拟组合优化问题,将内能 E E E 模拟为目标函数值 f f f,温度 T T T演化成控制参数 t t t,即得到解组合优化问题的SAA:
由初始解 x x x 和控制参数初值 t t t 开始,对当前解重复 "产生新解 --> 计算目标函数差 --> 接受或舍弃" 的迭代,并逐步衰减 t t t 值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡洛迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表控制,包括控制参数的初值 t t t 及其衰减因子 Δ t Δt Δt、每个 t t t 值时的迭代次数 L L L 和停止条件 S S S等。

2. 细节梳理
2.1 超参数的选择
初始温度T建议选择较大的值,终止温度T_end建议选择较小的值,这里选择初始温度T=100, T_end=0.001,过大或过小会影响算法收敛的速度;每个温度下的迭代次数和冷却系数可以根据问题场景适当控制,过大也会影响收敛的速度;玻尔兹曼常数k这里设置为1。
2.2 一些trick
其实,也可以不必完全按照上述流程图来实现SAA,比如,每个温度下的迭代次数,从原理上来看,这部分是影响了迭代次数,如果将冷却系数设置为稍大一些,比如0.99,那么这部分在实现的时候可以省略掉,算法仍然能够得到最优解。当然啦,博主只是在该问题上得出的一个结论,是否具有普适性还需要验证。本篇为了算法的完整性,仍然按照流程图来实现SAA算法。
3. 算法实现
3.1 问题场景
最值问题,求解 f ( x ) = x s i n ( 5 x ) − x c o s ( 2 x ) f(x) = xsin(5x) - xcos(2x) f(x)=xsin(5x)−xcos(2x)在定义域[0, 5]上的最小值。我们先手动计算一下:
f ′ ( x ) = 2 x s i n ( 2 x ) + s i n ( 5 x ) − c o s ( 2 x ) + 5 x c o s ( 5 x ) f^\prime (x) = 2 x sin(2 x) + sin(5 x) - cos(2 x) + 5 x cos(5 x) f′(x)=2xsin(2x)+sin(5x)−cos(2x)+5xcos(5x) 令 f ′ ( x ) = 0 f^\prime (x) = 0 f′(x)=0之后,理论上可以求得驻点,但又不太好计算。。。
3.2 从算法角度分析
根据上述问题场景及算法原理,需要考虑两种情况:
(1)当前解是局部最优解,即 f ( x ′ ) < f ( x ) f(x^ \prime) < f(x) f(x′)<f(x),保留当前局部最优解,继续产生新解;
(2)当前解非局部最优解,即 f ( x ′ ) ≥ f ( x ) f(x^ \prime) \geq f(x) f(x′)≥f(x),计算出当前温度下该解收敛的概率,如果概率大于一定阈值(随机的),则该解可以作为局部最优解,保留该解并继续产生新解,否则就丢弃该解,继续产生新解。
3.3 python实现
# -*- coding:utf-8 -*-
# Author: xiayouran
# Email: youran.xia@foxmail.com
# Datetime: 2023/1/16 11:12
# Filename: sa.py
import numpy as np
from matplotlib import pyplot as pltdef f(x):return x*np.sin(5*x) - x*np.cos(2*x)seed = 10086
np.random.seed(seed)T = 100 # 初始温度
T_end = 1e-3 # 终止温度
coldrate = 0.9 # 冷却系数
max_count = 15 # 每个温度值下的迭代次数
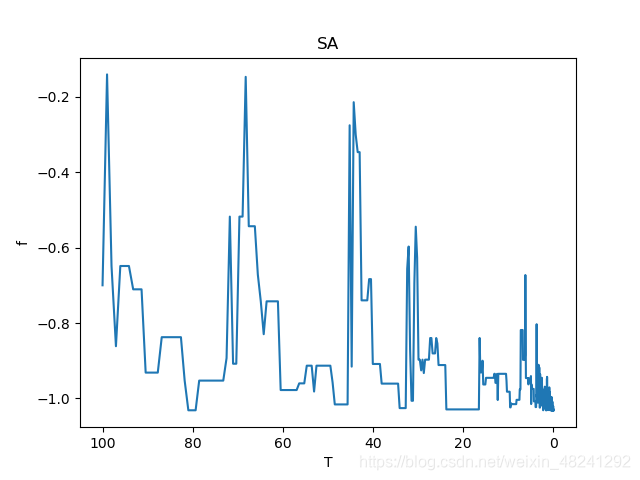
x_range = [0, 5] # 定义域if __name__ == '__main__':plt.figure()plt.ion()x_ = np.linspace(*x_range, num=200)plt.plot(x_, f(x_))x = np.random.uniform(*x_range) # 初始解while T > T_end:for _ in range(max_count):y = f(x)x_new = np.clip(x + np.random.randn(), a_min=x_range[0], a_max=x_range[1])# something about plottingif 'sca' in globals() or 'sca' in locals():sca.remove()sca = plt.scatter(x, y, s=100, lw=0, c='red', alpha=0.5)plt.pause(0.01)y_new = f(x_new)if y_new < y: # 局部最优解x = x_newelse:p = np.exp(-(y_new - y) / T) # 粒子在温度T时趋于平衡的概率为exp[-ΔE/(kT)]r = np.random.uniform(0, 1)if p > r: # 以一定概率来接受最优解x = x_newT *= coldrateplt.scatter(x, f(x), s=100, lw=0, c='green', alpha=0.7)plt.ioff()plt.show()print('最小值对应的坐标点: ({}, {})'.format(x, f(x)))
得到的最优解如下:
最小值对应的坐标点: (3.435632058805234, -6.276735466829619)
模拟过程如下:

代码仓库:IALib[GitHub]
本篇代码已同步至【智能算法(Python复现)】专栏专属仓库:IALib
运行IALib库中的SAA算法:
git clone git@github.com:xiayouran/IALib.git
cd examples
python main.py -algo saa