-
模拟退火算法的物理模型
在物理退火过程中,当固体的温度很高时,内能较大,固体内部的粒子处于无序运动状态,当温度慢慢降低时,固体的内能减小,粒子的运动趋于有序,如果温度降低得足够慢,在每个温度下粒子都会保持一个平衡状态,最终,当固体处于常温时,内能达到最小,此时粒子最为稳定。
模拟退火算法从初始温度出发(初始温度为较高温度),伴随着温度下降,目标函数的解趋于稳定(能量最低点),但是,这个稳定的解可能是局部最优解,因此,当到达一个较差的解时,算法会以一定的概率接受差解,从而跳出局部最优解,以寻找目标函数的全局最优解。
为了找到全局最优解,即能量最低点,设在温度下降的过程中,粒子的前一状态为x(n),通过邻域函数(也称状态产生函数,在某状态空间以某一概率密度函数随机采样跳转到下一状态)改变粒子的状态,变为x(n+1)。相应的,系统能量也由E(n)变为E(n+1)。当E(n+1)<E(n)时,系统能量减小了,我们以概率为1接受转换的状态(较优解);当E(n+1)>E(n)时,系统能量增大了,认为该状态偏离了全局最优位置(能量最低点),为差解,但是为了跳出局部最优解,算法不会立刻抛弃差解,而会以一定的概率 接受差解,当在区间[0,1]内产生的一个均匀分布的随机数小于p时,接受差解,即接受转换后的状态,否则拒绝接受。继续降温(降温可以降低接受差解的概率p),通过邻域函数改变粒子状态,判断是否接受下一状态,直到到达终止条件(终止条件可设最低温,也可设迭代的轮次)。 -
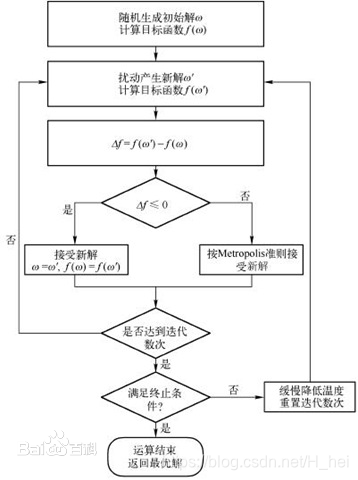
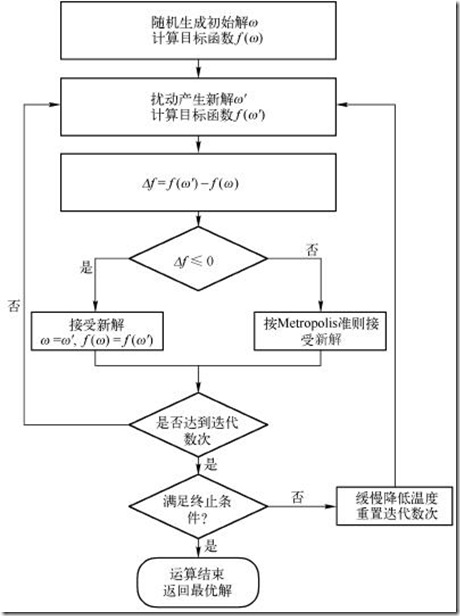
算法流程图

-
针对函数优化问题对模拟退火算法进行性能改进的方法和思路以及代码实现
以求解测试函数
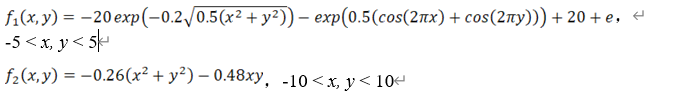
的最小值为例,(资料显示两个函数的最小值都为f(0,0)=0),函数f1的图像如图3-1-1所示,函数f2的图像如图3-1-2所示。


根据图2-1模拟退火算法的算法流程图编写如附录中表1所示的求解函数f1(x,y)最小值的程序清单,改进之处已在该程序清单中修改(求解函数f2的程序清单相似)。
在运行该程序时,为了获得更优解,我尝试了以下几种方法:
(1) 选择合适的初始值。
初始值包括初始温度,最低温度和初始状态。
在这个例子中,对于初始状态有两种方法,方法一是在定义域内随机生成初始状态;方法二是先随机生成一组状态,取求得的目标函数值最小的状态,两种方法的对比如表3-1-1所示。方法二虽然能获得较优的解,但在初始化的选择目标函数值最小时的状态时,容易后续操作导致陷入局部最优。
对于初始温度来说,当然是和最低温相差越大越好,但是在多次运行的情况下,不论温差有多大,仍有些解无法达到全局最优。
(2) 选择合适的邻域函数。
在本例中,我分别选取了正态分布和随机分布作为领域函数,在多次运行后,随机分布算出来的最小值整体上偏大于正态分布的算出来的最小值。
而选择正态分布作为邻域函数时还要注意调整方差,方差设置得较大,容易跳出最优解,方差设置得较小,又容易陷入全局最优。在多次尝试不同函数后,可以看出方差的选取和函数的定义域有关,定义域较大时,方差也应较大。在本例中,由于定义域较小,选取的方差为2。
(3) 选择合适的降温方式。
降温的作用是降低接受差解的概率,温度下降太快会导致难以跳出局部最优,在本例中,采用书本中经典模拟退火算法的降温方式。
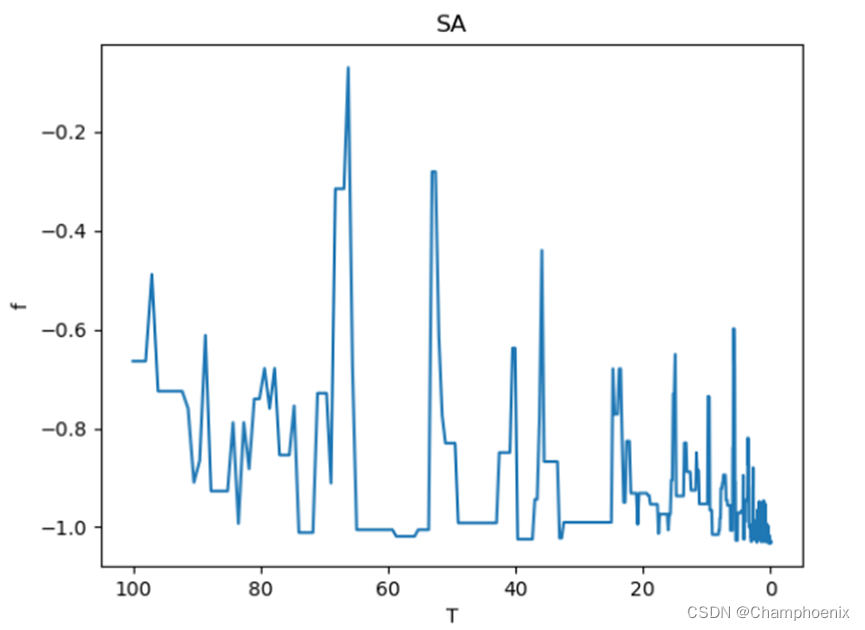
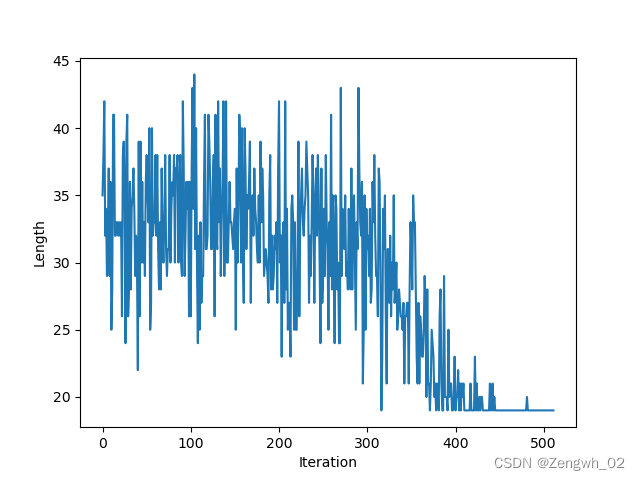
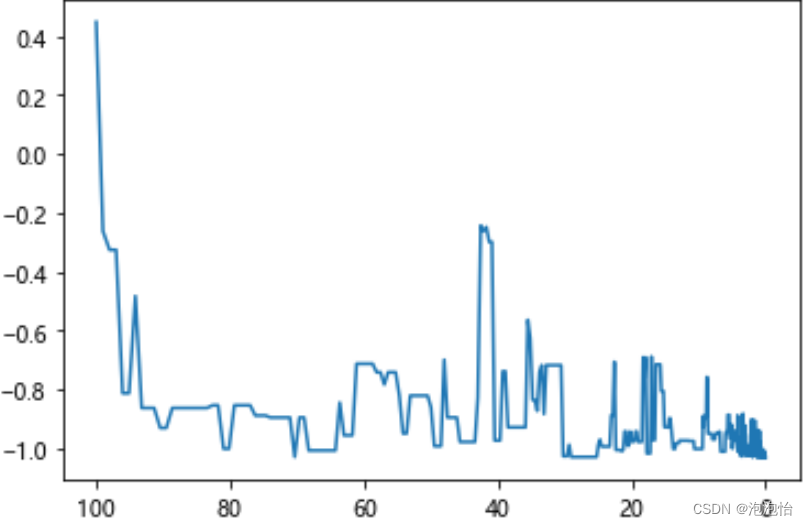
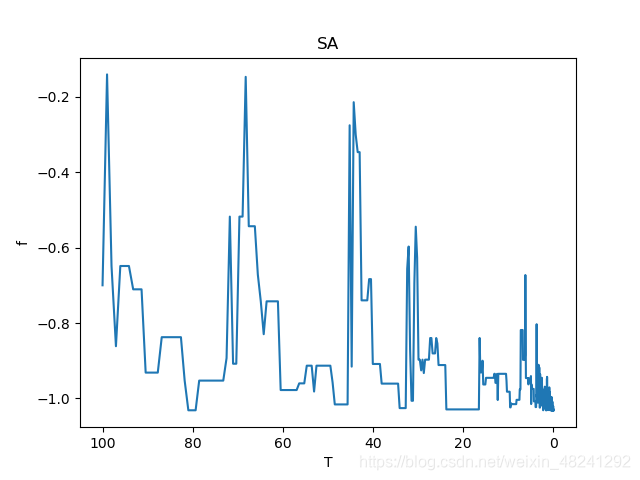
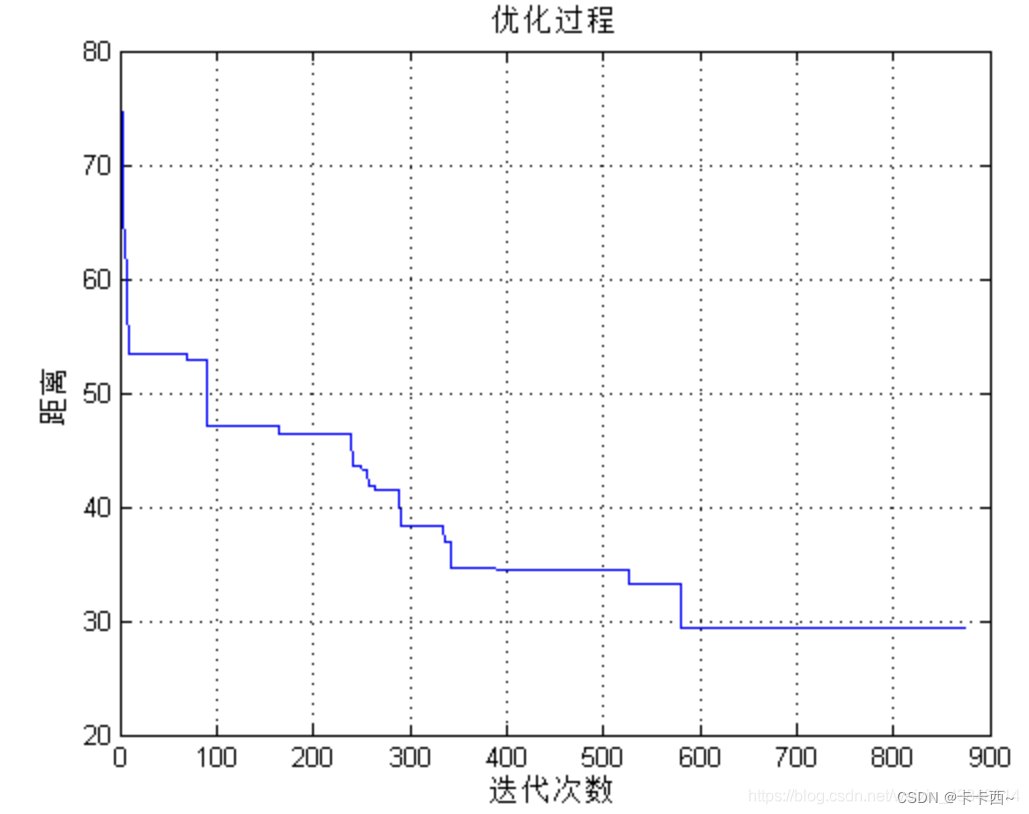
按照以上三个方法调整后,f2多次运行,大概率能获得较好的最低值,而由于f1有较多局部最优解,多次运行的结果大多仍然很难跳出局部最优或跳出了局部最优,又陷入了另一个局部最优。f1和f2在迭代过程中对解的记录曲线如下图3-3、图3-4所示。由两个图看出,算法还需要改进,因此,我又做了如(4)所示的调整。


(4) 记录最优解。
从图3-3、图3-4中不难看出,在迭代过程中,算法跳出了在该迭代中目标函数的最优解,为了不错过全局最优解,可以在迭代的过程中把较优解记录下来,迭代完成后和最后一个解进行比较,解的值低的作为最优解输出。
改进后运行分别一次求解f1和f2最小值的程序,控制台的输出结果如图3-5、图3-6所示。

-
测试代码
import numpy as np
import matplotlib.pyplot as plt
import math
import random
from scipy.stats import norm
from mpl_toolkits.mplot3d import Axes3D# 目标函数
def Function(x, y):return -20 * np.exp(-0.2*np.sqrt(0.5*(x*x+y*y)))\-np.exp(0.5*(np.cos(2*np.pi*x)+np.cos(2*np.pi*y)))+20+np.e# 初始化状态
def initN(low, high):'''随机生成一组状态取能量最低的状态:param low::param high::return:'''x = random.uniform(low, high)y = random.uniform(low, high)z = Function(x, y)for i in range(20):x1 = random.uniform(low, high)y1 = random.uniform(low, high)z1 = Function(x1, y1)if z1 < z:x = x1y = y1z = z1return x, y# 绘制目标函数
def figureFuc(low, high):X = np.linspace(low, high, 500)Y = np.linspace(low, high, 500)XX, YY = np.meshgrid(X, Y)Z = -20 * np.exp(-0.2*np.sqrt(0.5*(XX*XX+YY*YY)))\-np.exp(0.5*(np.cos(2*np.pi*XX)+np.cos(2*np.pi*YY)))+20+np.efig = plt.figure()ax = Axes3D(fig)ax.plot_surface(XX, YY, Z, cmap=plt.get_cmap('rainbow'))plt.show()# Metropolis准则接受新解
def Metropolis(detaF, T): # detaF为f(n+1) - f(x)if detaF < 0:return 1else:pTk = math.exp(-detaF/T)if pTk > random.random():return 1else:return 0# 利用正态分布产生新解
def get_normal_random_number(x,y,scale): # 正态分布''':param x: 均值:param y: 均值:param scale: 方差:return:'''fx = np.random.normal(x, scale)x = norm.ppf(fx)fy = np.random.normal(y, scale)y = norm.ppf(fy)return x, y# 利用均匀分布产生新解
def get_uniform_random_number(low, high):''':param low::param high::return:'''x = np.random.uniform(low, high)y = np.random.uniform(low, high)return x, y# 冷却函数
def descT(T, k):# return T/np.log(1 + k)return 0.9*T# 主函数
def startMain():# 初始化low = -5high = 5T = 10000Tmin = 10k = 1# figureFuc(low, high) # 画图#x = random.uniform(low, high)#y = random.uniform(low, high)x, y = initN(low, high)z = Function(x, y)min_value = zrecord_value = [] # 用数组记录被接受的新解并绘图,方便分析while(T > Tmin and k <= 1000):x1, y1 = get_normal_random_number(x, y, 2) # 利用正态分布产生新解# x1, y1 = get_uniform_random_number(low, high) # 利用随机分布产生新解if x1 < low or x1 > high or y1 < low or y1 > high: # 新解不在定义域内时跳出本次循环breakz1 = Function(x1, y1) # 计算新解的目标函数值deltaE = z1 - zmin_value = min(min_value, z1)if Metropolis(deltaE, T) == 1: # 接受按照Metropolis准则接受新解x = x1y = y1z = z1record_value.append(z)if deltaE > 0:T = descT(T, k)else:k += 1print('迭代到组后的解:', z)print('记录下的最优解:', min_value)# 打印解的变化曲线x=[i+1 for i in range(len(record_value))]plt.plot(x, record_value)plt.show()if __name__ == "__main__":startMain()