模拟退火算法
- 提出问题
- 青铜级别解法(盲目搜索)
- 王者级别解法(启发式搜索)
- 操作方法
- 需要研究的地方
- 如果这个优化问题有约束条件怎么办?
- 这个C~t~怎么设置?
- t的变化在编程里面怎么实现?
- 什么时候停止搜索?
- 怎么在A附近随机生成一个新解B?
- 题目1:求给定函数的最大值或者最小值
- 问题2:旅行商问题
- 书店买书问题
- 背包问题
提出问题
(1)求一个给定函数的最值问题
eg:求函数 y = 11 s i n x + 7 c o s ( 5 x ) y=11sinx+7cos(5x) y=11sinx+7cos(5x)在[-3,3]内的最大值
第一反应:暴力搜索?啊…这…如果有30个变量怎么办?
(2)TSP(旅行商问题)
eg:一个售货员必须访问n个城市,这n个城市是一个完全图,售货员需要恰好访问所有城市的一次,并且得到最终的城市。城市与城市之间有一个旅行费用,售货员希望旅行费用最少。
完全图:完全图是一个简单的无向图,其中每对不同的顶点之间都恰有一条边框相连。
 (3)书店买书问题(假设有m个书店,n本书,那么买书的方案有mn种)
(3)书店买书问题(假设有m个书店,n本书,那么买书的方案有mn种)
某同学要从六家线上商城选购5本书籍B1,B2,B3,B4,B5,每本书籍在不同商家的售价及其每个商家的单次运费险如下表所示,请给该同学制定最省钱的选购方案。(注:在同一个书店买多本书也只会收取一次运费)
 (4)背包问题(如果有n件货物,那么可能性有2n种)
(4)背包问题(如果有n件货物,那么可能性有2n种)

上述的这些问题,均是求某一目标函数的最值问题。(某一给定的函数、旅行的路程或费用、买书的花费、利润)
MATLAB中所求出的是最小值,在求最大值时候可以给目标函数添加符号等方法转化成求最小值问题。
青铜级别解法(盲目搜索)
1. 蒙特卡洛模拟
2. 对比穷举法
但在解空间的可能情况特别多时,这两种方法就凉凉。
王者级别解法(启发式搜索)
模拟退火算法(以一定概率接受新的解)
求函数 y = 11 s i n x + 7 c o s ( 5 x ) y=11sinx+7cos(5x) y=11sinx+7cos(5x)在[-3,3]内的最大值
旧的解:xi对应的函数值f(xi)
新的解:在xi“附近”随机寻找一个新的解xj,对应的函数值为f(xi)
- 如果f(xj)>f(xj),则接受新解xj;
- 如果f(x)≤f(xi),我们不能直接拒绝xj;
解决方法: 为了不直接拒绝xj,我们定义一个接受的概率p,p位于[0,1]之间,且f(xj)和f(xi)越接近,p越大。(意思就是,新解和旧解的函数值越接近,我们就越愿意接受新解。)
即p正比于 1 ∣ f ( x j ) − f ( x i ) ∣ \frac{1}{|f(x_j)-f(x_i)|} ∣f(xj)−f(xi)∣1,记为p∝ 1 ∣ f ( x j ) − f ( x i ) ∣ \frac{1}{|f(x_j)-f(x_i)|} ∣f(xj)−f(xi)∣1
接着思考:概率p位于[0,1]之间,哪个常见的函数值域是位于[0,1]之间的?
不唯一,但有一个函数形式很简单: y = e − x ( x ≥ 0 ) y=e^{-x}(x≥0) y=e−x(x≥0),关于x单调递减:
 所以我们可以假设: p ∝ e − ∣ f ( x j ) − f ( x i ) ∣ p∝e^{-|f(x_j)-f(x_i)|} p∝e−∣f(xj)−f(xi)∣
所以我们可以假设: p ∝ e − ∣ f ( x j ) − f ( x i ) ∣ p∝e^{-|f(x_j)-f(x_i)|} p∝e−∣f(xj)−f(xi)∣
- 接受新解的概率p越大,意味着在解空间中搜索的范围越大
原因:接受新解的概率p越大,意味着我们的搜索更容易接受不好的解,这时候就相当于增加了我们的搜索范围。
- 假设我们将搜索过程看作一个“工序”,那么搜索前期,我们的搜索范围应该尽量的大,搜索后期我们的搜索范围应该尽量的小。
原因:在搜索前期,我们要尽可能的扩大我们的搜索范围,这样能够避免陷入局部最优解;在搜索后期我们要倾向于局部搜索。(渣男套路:前期广撒网、后期精准打击)
我们对式子 p ∝ e − ∣ f ( x j ) − f ( x i ) ∣ p∝e^{-|f(x_j)-f(x_i)|} p∝e−∣f(xj)−f(xi)∣进行一个变形:
p t ∝ e − ∣ f ( x j ) − f ( x i ) ∣ × C t p_t∝e^{-|f(x_j)-f(x_i)|×C_t} pt∝e−∣f(xj)−f(xi)∣×Ct
- 其中:Ct可以看作一个和时间有关的系数,因此在搜索过程中,我们接受新解的概率p就和时间有关,显然时间越长,Ct越大
原因:搜索前期t较小,我们希望搜索的范围大,即更倾向于接受新解,那么对应的p就应该大一些,而Ct与p负相关,因此Ct应该小一点;搜索后期我们希望p较小,那么Ct应该大一点,因此我们可以得出结论:Ct关于t递增。
操作方法
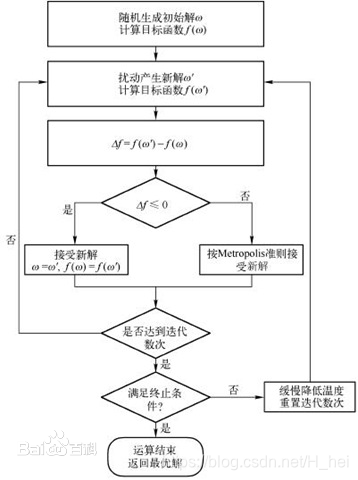
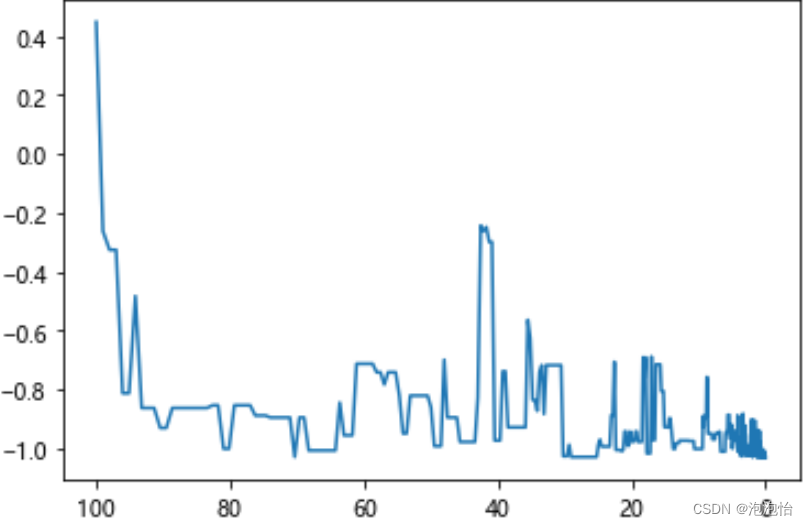
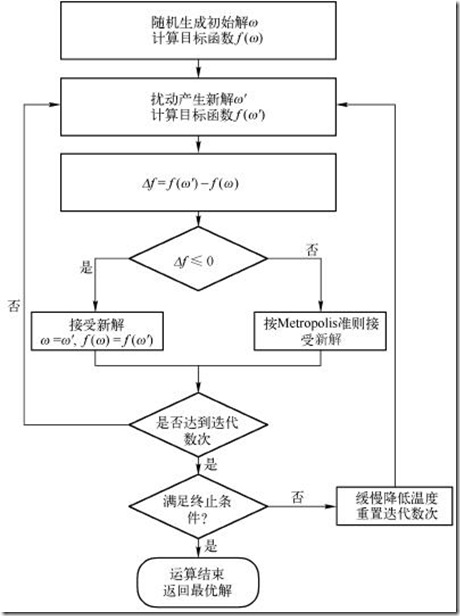
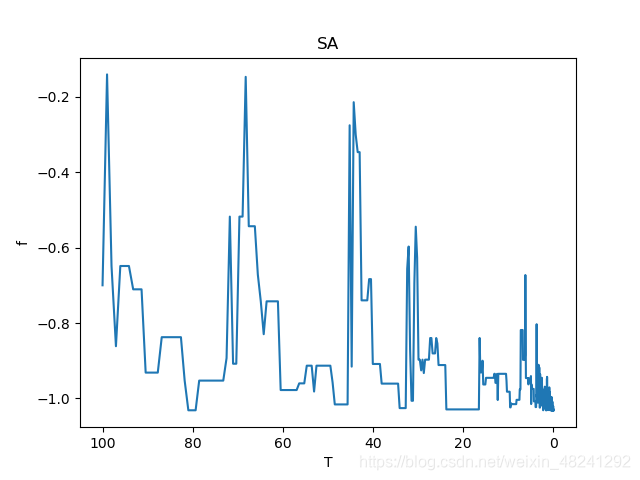
我们的搜索过程(假设求最大值问题)可以用下面这个简单的流程表示:
- 随机生成一个解,计算解A对应的目标函数值f(A)
- 在A附近随机产生一个解B,计算解B对应的目标函数值f(B)、
- 如果f(B)>f(A),那么将解B的值给解A,然后重复上面步骤(爬山法的思想);
如果f(B) ≤ f(A),那么我们接受B的概率为 p t = ∝ e − ∣ f ( x j ) − f ( x i ) ∣ × C t p_t=∝e^{-|f(x_j)-f(x_i)|×C_t} pt=∝e−∣f(xj)−f(xi)∣×Ct,然后我们生成一个[0,1]之间的随机数r,如果r<p,我们就将解B赋值给解A,然后重复上面的步骤;否则我们返回第2步,在原来的A附近再重新生成一个解B,然后继续下去。
需要研究的地方
如果这个优化问题有约束条件怎么办?
编写一个筛选随机数的程序就好啦。
这个Ct怎么设置?
定义初始温度T0=100,温度下降的公式为:Tt+1=αTt,α常取0.95,那么时刻t时的温度:Tt=αT0=100×0.95t.
取 C t = 1 T t = 1 100 × 0.9 5 t C_t=\frac{1}{T_t}=\frac{1}{100×0.95^t} Ct=Tt1=100×0.95t1,那么 p t = ∝ e − ∣ f ( x j ) − f ( x i ) ∣ 100 × 0.9 5 t p_t=∝e^{-\frac{|f(x_j)-f(x_i)|}{100×0.95^t}} pt=∝e−100×0.95t∣f(xj)−f(xi)∣
注意:这里的倒数是为了保证Ct关于t递增。
p t = ∝ e − ∣ f ( x j ) − f ( x i ) ∣ T t p_t=∝e^{-\frac{|f(x_j)-f(x_i)|}{T_t}} pt=∝e−Tt∣f(xj)−f(xi)∣
记 Δ f = ∣ f ( B ) − f ( A ) ∣ Δf=|f(B)-f(A)| Δf=∣f(B)−f(A)∣
那么p到底有多大呢?

- 温度一定时,Δf越小,概率越小,即目标函数相差越小接受的可能性越大。
- Δf一定时,温度越高,概率越大,即搜索前期温度较高时更有可能接受新解。
t的变化在编程里面怎么实现?
- 可以看成我们迭代的次数。(采用循环)
t表示时间,迭代第一次,迭代第二次,t从1到1000,就迭代1000次。 - 为了保证搜索过程的彻底,在同一温度下(同一个小t),我们需要进行多次搜索(例如重复上面的流程500次);之后我们降低温度,然后再来进行新的一轮搜索。
用编程的话是由两层循环。
什么时候停止搜索?
有很多种准则:
- 达到指定的迭代次数,例如迭代200次;
- 达到指定的温度,例如温度小于0.000001;
- 我们找到最优解连续M次(例如30次)迭代都没有变化。
怎么在A附近随机生成一个新解B?
题目1:求给定函数的最大值或者最小值
我们以n元函数求最值为例,来介绍新解的产生规则:
假设当前解为:(x1,x2,…,xn)
我们首先生成一组随机数(y1,y2,…,yn),其中yi服从N(0,1)
[均值为0,方差为1的正态分布]
接下来我们再计算(z1,z2,…,zn)其中 z 1 = y / y 1 2 + y 2 2 + … + y n 2 z_1=y/\sqrt{y_1^2+y_2^2+…+y_n^2} z1=y/y12+y22+…+yn2
[对随机数进行标准化]
对于每一个i∈[1,n],来产生一个新解,即进行下面操作:
- 计算:xinew=xi+T×zi,T是当前的温度(也可以使用xinew=xi+ T \sqrt{T} T×zi);
- 接下来检查xinew是否位于上下界内,即是否满足lbi≤xinew≤ub这个约束:
a.如果lbi≤xinew≤ub满足,则直接令xj=xinew即可;
b.如果xinew<lbi,则 x j = r × l b i + ( 1 − r ) × x i n e w x_j=r×lb_i+(1-r)×x_i^{new} xj=r×lbi+(1−r)×xinew这里r是区间[0,1]上均匀分布的随机数;
c.如果xinew>ubi,则 x j = r × u b i + ( 1 − r ) × x i n e w x_j=r×ub_i+(1-r)×x_i^{new} xj=r×ubi+(1−r)×xinew这里r是区间[0,1]上均匀分布的随机数。
b和c的处理方式就相当于数据太大或太小需要折中。
这是MATLAB内置函数的定义方法。
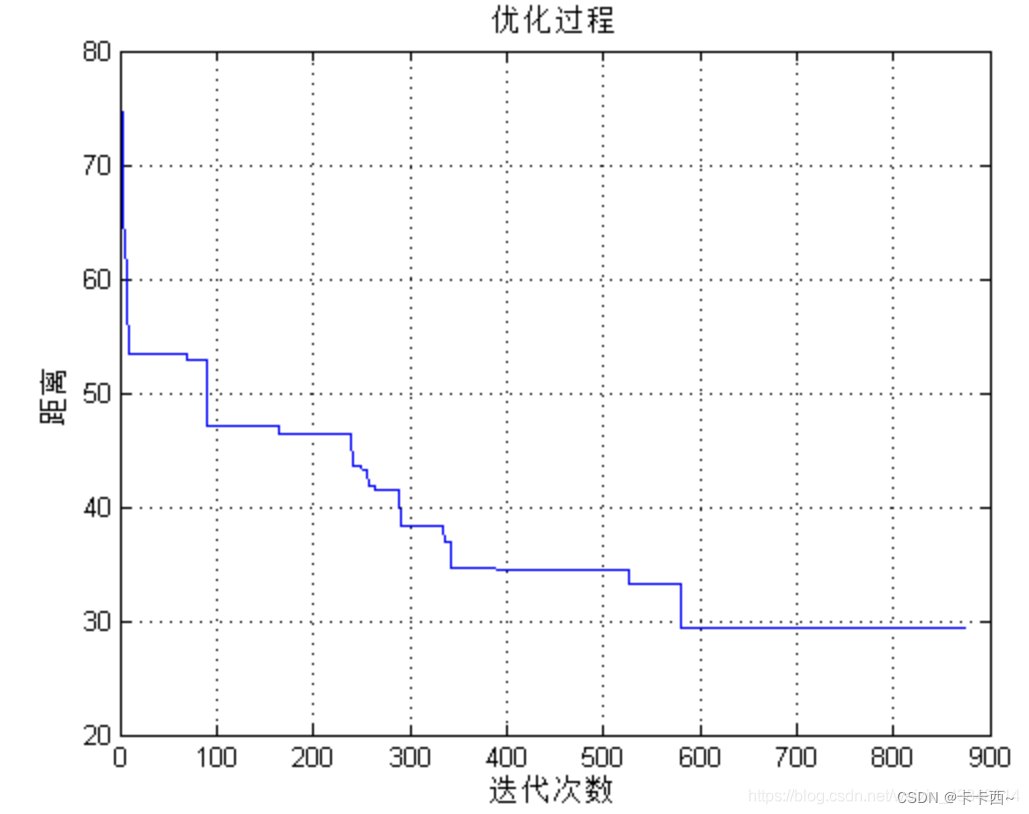
问题2:旅行商问题
问题的内容:给定一系列城市和每对城市之间的距离,求解访问每座城市一次并回到起点的最短回路。
三种产生新解的方法:

书店买书问题

背包问题