优化模拟退火算法
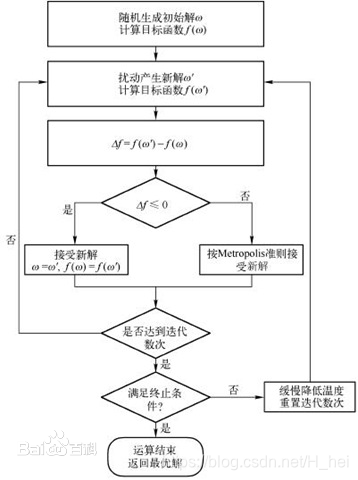
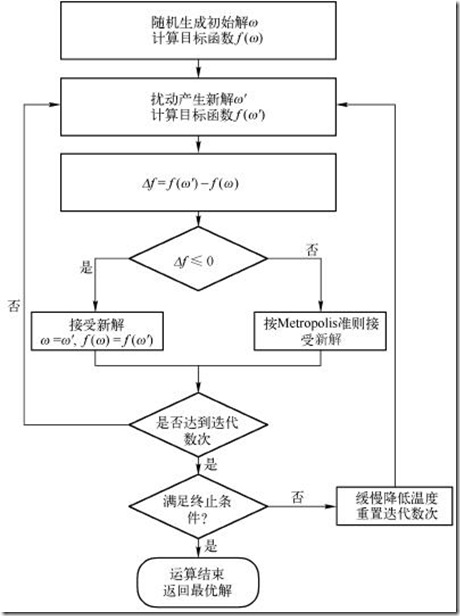
作为现代算法的一种,模拟退火算法是一种用降低搜索的覆盖面积来提高运算速度的算法,适用于解决各种优化类问题。它利用了物理学中一个常见的原理:当物体具有一定的温度时,假设它内部含有的能量为E(I),那么物体从I状态进入J状态符合以下规则:
若E(i)>E(j),则该状态改变被接受。
若E(i)<E(j),则该状态有e^((E(i)-E(j))/KT)的概率被接受。
在进行了充分的转换后材料将达到热平衡。这时候材料处于状态i的概率为
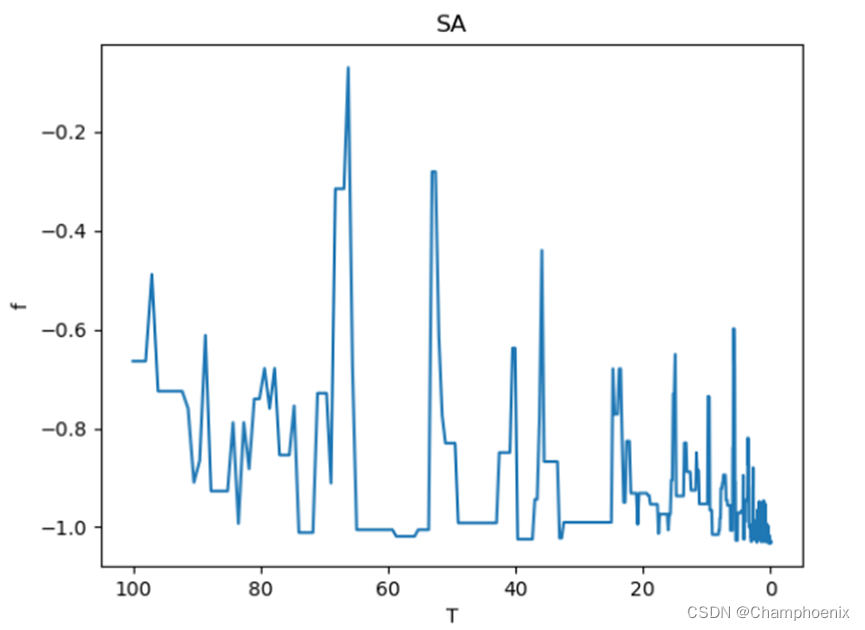
通过对概率的化简可以推导出所有状态在高温下具有相同的概率,而当温度下降的时候,材料会以很大概率进入最小能量状态。
通过对概率的化简可以推导出所有状态在高温下具有相同的概率,而当温度下降的时候,材料会以很大概率进入最小能量状态。
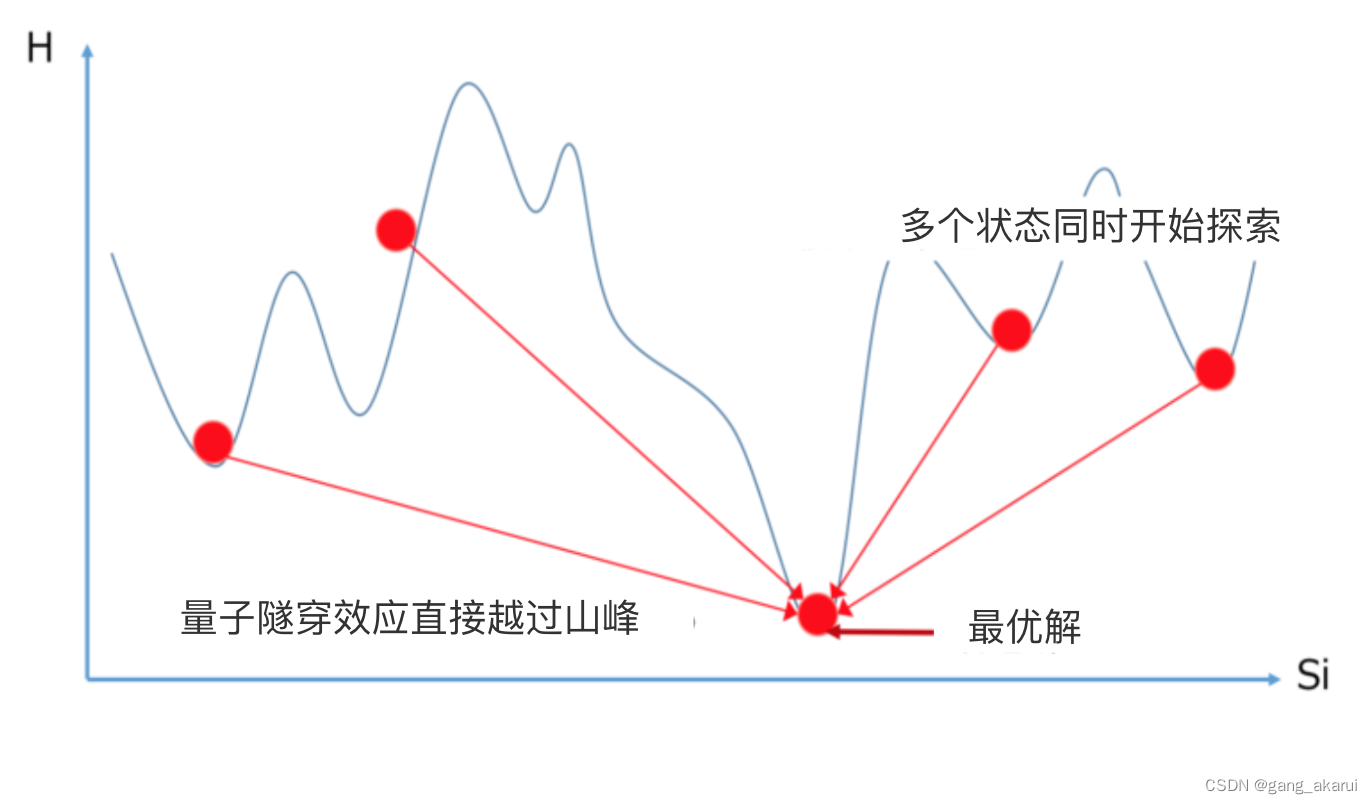
简单来说 ,就像是我们想去到一群山脉中的最高峰,一般来讲采用的规则是:当到达了一定高的地方,我们把它和周围的山峰进行比较,当周围的山明显比自己所处的山高时,会毫不犹豫的向哪里进发,但是有的山很难判别是否更高,所以我们有一定的概率去那里,在这种算法中,我们赋予的概率是e^((E(i)-E(j))/KT)。
举个例子
如果有一个软件,记录了我们达到的最高海拔,就比如A最高到达过这片山峰的最顶峰,那么他现在有可能在这片山脉中的任何位置,但是C最高在山脚,所以他只可能在山脚。 
模拟退火算法的本质是一个穷举加比较的算法,通过穷举来递推函数并通过比较进行舍弃,但是很明显的它也存在问题:很多时候它对于区间的舍弃都太过粗糙,很有可能因为抽到的点数值不高而导致这一个区域被淘汰。
在学习的同时,我意识到对数值进行舍弃的目的是为了得到极大值,而得到极大值的方法除了穷举-比较-舍弃之外还有排序直接得出,但是排序的问题很明显:他会消耗很大的计算量和计算时间,但是只对局部进行排序效果肯定没有穷举比较舍弃好,所以我开始研究排序算法的优化问题。
**
排序算法的优化问题
对常用的排序算法,我们常用插入排序:每一个数都要从头开始比较一遍来找到相应的位置,这里我用分析算法来度量一个算法所用的代价,为了方便理解我用伪代码进行编写
假设对j=2,3,…,n,其中n=A.length,假设t_j表示对那个值j执行while循环测试的次数
*
*对算法的总代价进行求和:

当情况最好,也就是说所有的数值都已经被排好的时候,i取j-1,t_j=1,运行的最佳时间为:T(n)=(c1+c2+c4+c5+c8)n-(c2+c4+c5+c8)
很明显的可以看出来这是一个由n决定的线性函数,但是如果数组本来是反向排列,它所需要的代价是:
(c5/2+c6/2+c7/2)n^2+(c1+c2+c4+c5/2-c6/2-c7/2+c8)n-(c2+c4+c5+c8)
这是一个关于n的二次函数。
但是平均算法往往更接近最坏的情况,所以可以认为决定排序算法代价的主要是一个二次函数,因此在考虑算法优化的时候,我们更因该先考虑最坏情况。
回到本质,我认为排序算法可以优化的地方在于有的数并没有必要比那么多次,因为只要确定它大于某一个数就可以确定比这个数之前的数都大,尤其是数据容量比较大的时候,它对程序运行代价的减少就更为明显。同时我还注意到了当n足够大的时候,〖(n-1)〗2比n2要小的很多,这就说明只要我找到一个办法让被分开的数组进行排序且这种办法的代价是一次方式,就可以对排序算法进行比较大的优化。
假设我们的数组是一堆牌,我们将牌分为俩堆排好序,这时候我们对每堆最大的进行比较,较大的放出来,继续比较,直到某一堆见底,就将剩下的一堆全部放进去。从程序上来说,这种过程进行的是重复的比较-删除-比较,如果对设计的比较好甚至可以省去循环的过程,毫无疑问这是一个一次函数。
通过简化,优化后的排序算法结构大致如下:
1.将数组分为俩组,并对每组进行排序
2.对每组的最大值进行比较,选出最大的拿出来
3.继续比较
3.1.当一个组见底后另一个组剩下的直接放入
随机算法
这种方法对于排序算法来讲是一个优化,但是回到问题本身,我们的目标是将排序算法带入模拟退火算法来进行优化,但是首先,模拟退火算法是一个优化类算法,它并没有一个特定的数值解,所以并不存在最优解一说,因此它需要的排序也并不是有限个,而是从中抽取某些来进行排序。在这里我们就要面临另外一个问题:大部分时候,我们在进行递推的时候,我们采用的都是按数轴顺序,其实这种方法就是上面我说比较粗糙的原因所在,因为很多时候值的大小和所处的数轴位置是无关的,由此来说由某一个点舍弃这一片区域并不合理,虽然说当数值比较小的时候可以肉眼观察出来,但是当数值比较大,不足以画出图的时候,我们只能相信计算机的判断,这里我想到了一种随机算法来比较适用。
我们还是用例子来说明,假如公司雇人,一共有十个应聘者,你要从中找到最优秀的,但是每一个应聘者你要现场给他答复,如果收了还要给他签约费。类比一下,你要面对十个数,找到最大值,对每一个遇到的大的数你要消耗内存把他存起来和下一个比较。
假设十个人的能力分别是1-10,分三种情况来面试
- 能力从低到高,最亏的方法,要付十次签约费
- 能力从高到底,最赚的,只要付一次就可以选到最优秀的人
- 乱序,随机抽,所需在俩者之间。
确实第2种看起来是最优秀的,可是我们现实中面临的问题更多的是无序的问题(要不然也不需要算法来计算了),更何况我们并不需要取遍所有的数值。
注意:这里随机的并不是对函数结果随机取值,而是对函数的自变量的随机取值。
这种算法可以对模拟退火算法的哪个部分进行优化呢?我们先回顾模拟退火算法的三个步骤:
1.给出定义域
2.设计递推式
3.比较
毫无疑问第一步没有什么可以优化的空间,而优化后的排序算法可以代替第三步的比较过程,那么随机算法就是对设计递推式的优化了,具体表现在递推的时候不再是常规的时间顺序或者数轴顺序,而是利用计算机自带的伪随机算法来进行取值,这样可以充分的减少所需的代价。
遗传算法的局部优化
遗传算法和模拟退火算法一样属于近代优化算法的一种,大致上这些算法的区别在于对数值取舍比较方式不同,总的思路并没有什么巨大的变化,但是遗传算法中有一个步骤却是它独有的:变异。
变异是指选取某些结果的某个部分进行交换,这个看起来无厘头的举动。实际上却是在保证偏移程度不大的前提下扩大取值范围,举个例子:
假设正确的答案是1011001
而我们有的四个选项分别是
A.1100111 B.1000001 C.1100001 D.1111111
可以看见没有一个和正确答案很接近,但是如果对C和D的第二三四位进行所谓的变异(杂交)就可以得到1011001,同时因为本来给出的就是经过筛选的答案,所以并不会出现和正确答案越走越远的情况。
但是因为在变异算法里整体程序是按自然界的演化来进行的,所以变异可以很合适的融入进去。
之所以模拟退火算法并不适用于变异环节是因为它得到的往往是某一个解,而不是某一组解,因此也就没有所谓数据之间的演化和变异,但是前面提到的优化排序算法可以很好的解决这个问题,我们得到的解虽然在数轴上并不连续,但是是经过比较的、相对于某些解来说的优化解。这里我的思路分为俩种:
- 计算机性能足够的话,可以设计一个寻找这些解的共同点的算法,在寻找到共同点后对相异的部分进行交换,继续计算契合度。直到下一次递推的契合度比原来的低。
- 就和原本的方法一样,一定概率一定位置发生交换。这种情况很有可能没有什么显著的改变。
优化后的模拟退火算法
在进行优化后,我们从头到尾再看一遍模拟退火算法:
- 确定问题所处的区间/导入数值,这里并没有什么可以优化的部分
- 在选取自变量的时候利用电脑的伪随机来选取并算出具体结果
- 将得到的结果进行排序
- 视情况决定是否使用优化遗传算法来改变数值。
- 得到结果。