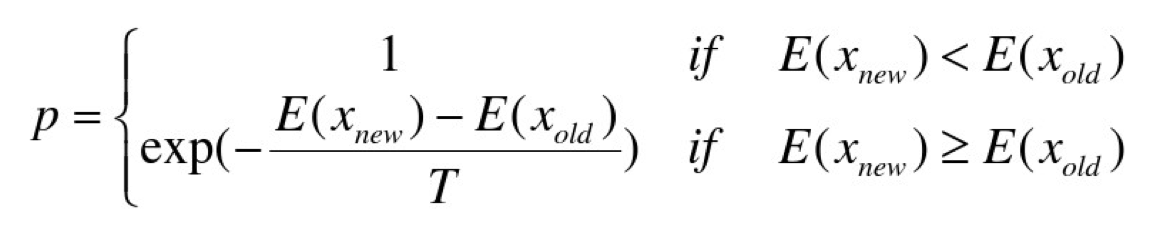本文转自https://www.cnblogs.com/ranjiewen/p/6084052.html

模拟退火算法

著名的模拟退火算法，它是一种基于蒙特卡洛思想设计的近似求解最优化问题的方法。

一点历史——如果你不感兴趣，可以跳过

美国物理学家 N.Metropolis 和同仁在1953年发表研究复杂系统、计算其中能量分布的文章，他们使用蒙特卡罗模拟法计算多分子系统中分子的能量分布。这相当于是本文所探讨之问题的开始，事实上，模拟退火中常常被提到的一个名词就是Metropolis准则，后面我们还会介绍。

美国IBM公司物理学家 S.Kirkpatrick、C. D. Gelatt 和 M. P. Vecchi 于1983年在《Science》上发表了一篇颇具影响力的文章：《以模拟退火法进行最优化（Optimization by Simulated Annealing）》。他们借用了Metropolis等人的方法探讨一种旋转玻璃态系统（spin glass system）时，发觉其物理系统的能量和一些组合最优（combinatorial optimization）问题（著名的旅行推销员问题TSP即是一个代表例子）的成本函数相当类似：寻求最低成本即似寻求最低能量。由此，他们发展出以 Metropolis 方法为本的一套算法，并用其来解决组合问题等的寻求最优解。

几乎同时，欧洲物理学家 V.Carny 也发表了几乎相同的成果，但两者是各自独立发现的；只是Carny“运气不佳”，当时没什么人注意到他的大作；或许可以说，《Science》杂志行销全球，“曝光度”很高，素负盛名，而Carny却在另外一本发行量很小的专门学术期刊《J.Opt.Theory Appl.》发表其成果因而并未引起应有的关注。

Kirkpatrick等人受到Metropolis等人用蒙特卡罗模拟的启发而发明了“模拟退火”这个名词，因为它和物体退火过程相类似。寻找问题的最优解（最值）即类似寻找系统的最低能量。因此系统降温时，能量也逐渐下降，而同样意义地，问题的解也“下降”到最值。

一、什么是退火——物理上的由来

在热力学上，退火（annealing）现象指物体逐渐降温的物理现象，温度愈低，物体的能量状态会低；够低后，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。大自然在缓慢降温（亦即，退火）时，可“找到”最低能量状态：结晶。但是，如果过程过急过快，快速降温（亦称「淬炼」，quenching）时，会导致不是最低能态的非晶形。

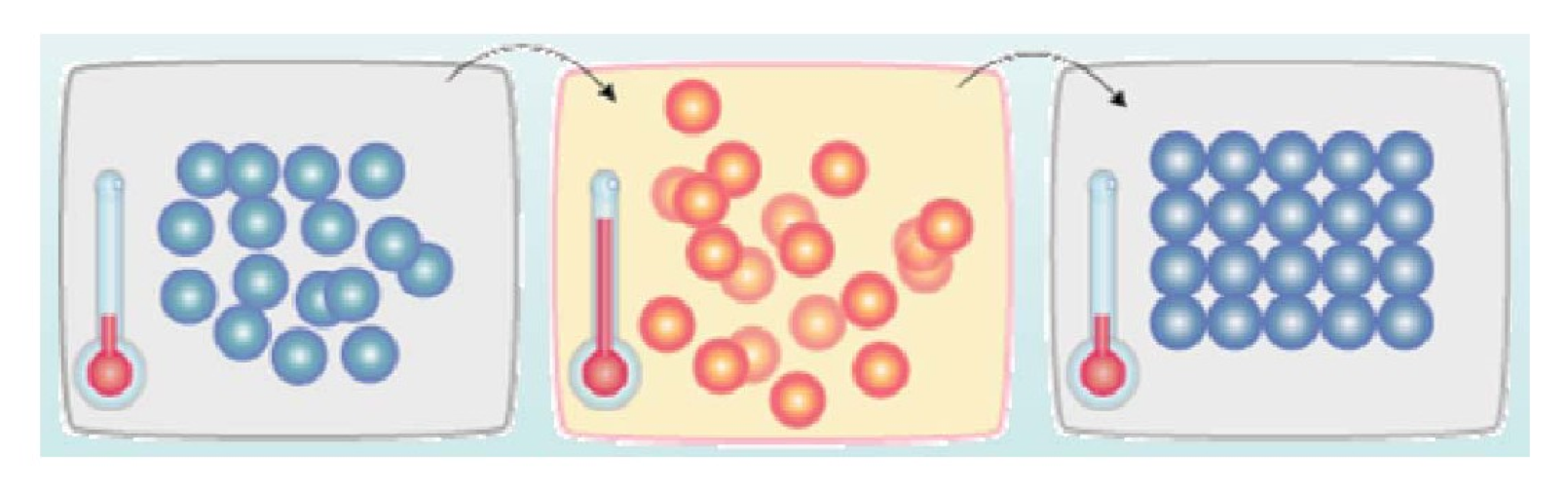
如下图所示，首先（左图）物体处于非晶体状态。我们将固体加温至充分高（中图），再让其徐徐冷却，也就退火（右图）。加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小（此时物体以晶体形态呈现）。

似乎，大自然知道慢工出细活：缓缓降温，使得物体分子在每一温度时，能够有足够时间找到安顿位置，则逐渐地，到最后可得到最低能态，系统最安稳。

二、模拟退火（Simulate Anneal）

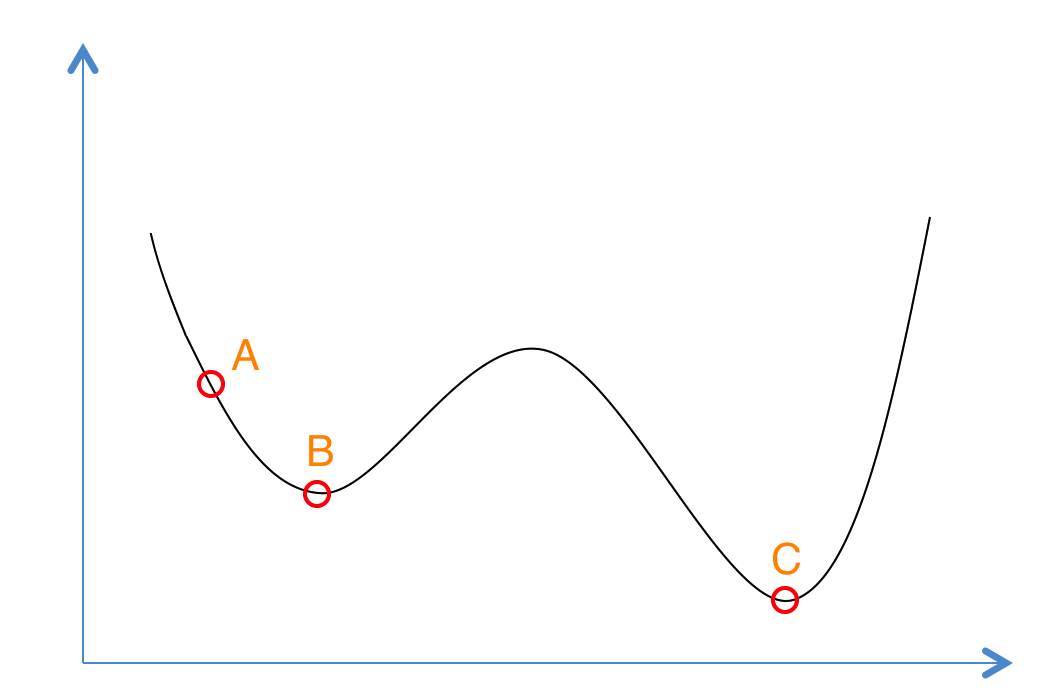
如果你对退火的物理意义还是晕晕的，没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数，现在想求函数的（全局）最优解。如果采用Greedy策略，那么从A点开始试探，如果函数值继续减少，那么试探过程就会继续。而当到达点B时，显然我们的探求过程就结束了（因为无论朝哪个方向努力，结果只会越来越大）。最终我们只能找打一个局部最后解B。

模拟退火其实也是一种Greedy算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解B后，会以一定的概率接受向右继续移动。也许经过几次这样的不是局部最优的移动后会到达B 和C之间的峰点，于是就跳出了局部最小值B。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为

Metropolis准则表明，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：P(dE) = exp( dE/(kT) )。其中k是一个常数，exp表示自然指数，且dE<0。所以P和T正相关。这条公式就表示：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（因为退火的过程是温度逐渐下降的过程），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低，P(dE)会逐渐降低。

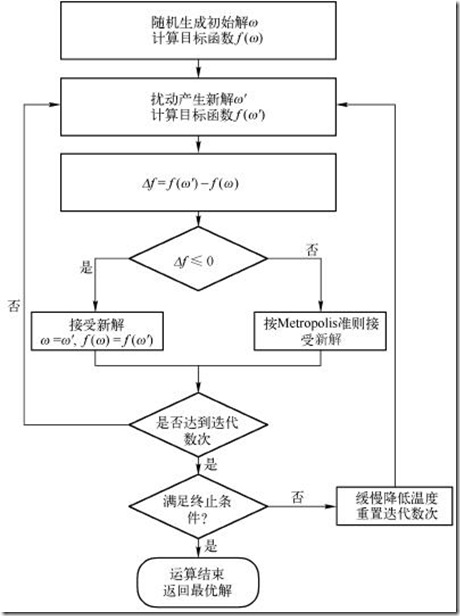
我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。也就是说，在用固体退火模拟组合优化问题，将内能E模拟为目标函数值 f，温度T演化成控制参数 t，即得到解组合优化问题的模拟退火演算法：由初始解 i 和控制参数初值 t 开始，对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代，并逐步衰减 t 值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。

总结起来就是：

若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解)，则总是接受该移动；
若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）相当于上图中，从B移向BC之间的小波峰时，每次右移（即接受一个更糟糕值）的概率在逐渐降低。如果这个坡特别长，那么很有可能最终我们并不会翻过这个坡。如果它不太长，这很有可能会翻过它，这取决于衰减 t 值的设定。

关于普通Greedy算法与模拟退火，有一个有趣的比喻：

普通Greedy算法：兔子朝着比现在低的地方跳去。它找到了不远处的最低的山谷。但是这座山谷不一定最低的。这就是普通Greedy算法，它不能保证局部最优值就是全局最优值。
模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向低处，也可能踏入平地。但是，它渐渐清醒了并朝最低的方向跳去。这就是模拟退火。

通过一个实例来编程演示模拟退火的执行。特别地，我们这里所采用的实例是著名的“旅行商问题”（TSP，Traveling Salesman Problem），它是哈密尔顿回路的一个实例化问题，也是最早被提出的NP问题之一。

TSP是一个最常被用来解释模拟退火用法的问题，因为这个问题比较有名，我们这里不赘言重述，下面直接给出C++实现的代码：

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stdio.h>
#include <time.h>
#include <math.h>#define N     30      //城市数量
#define T     3000    //初始温度
#define EPS   1e-8    //终止温度
#define DELTA 0.98    //温度衰减率#define LIMIT 1000   //概率选择上限
#define OLOOP 20    //外循环次数
#define ILOOP 100   //内循环次数using namespace std;//定义路线结构体
struct Path
{int citys[N];double len;
};//定义城市点坐标
struct Point
{double x, y;
};Path bestPath;        //记录最优路径
Point p[N];       //每个城市的坐标
double w[N][N];   //两两城市之间路径长度
int nCase;        //测试次数double dist(Point A, Point B)
{return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}void GetDist(Point p[], int n)
{for(int i = 0; i < n; i++)for(int j = i + 1; j < n; j++)w[i][j] = w[j][i] = dist(p[i], p[j]);
}void Input(Point p[], int &n)
{scanf("%d", &n);for(int i = 0; i < n; i++)scanf("%lf %lf", &p[i].x, &p[i].y);
}void Init(int n)
{nCase = 0;bestPath.len = 0;for(int i = 0; i < n; i++){bestPath.citys[i] = i;if(i != n - 1){printf("%d--->", i);bestPath.len += w[i][i + 1];}elseprintf("%d\n", i);}printf("\nInit path length is : %.3lf\n", bestPath.len);printf("-----------------------------------\n\n");
}void Print(Path t, int n)
{printf("Path is : ");for(int i = 0; i < n; i++){if(i != n - 1)printf("%d-->", t.citys[i]);elseprintf("%d\n", t.citys[i]);}printf("\nThe path length is : %.3lf\n", t.len);printf("-----------------------------------\n\n");
}Path GetNext(Path p, int n)
{Path ans = p;int x = (int)(n * (rand() / (RAND_MAX + 1.0)));int y = (int)(n * (rand() / (RAND_MAX + 1.0)));while(x == y){x = (int)(n * (rand() / (RAND_MAX + 1.0)));y = (int)(n * (rand() / (RAND_MAX + 1.0)));}swap(ans.citys[x], ans.citys[y]);ans.len = 0;for(int i = 0; i < n - 1; i++)ans.len += w[ans.citys[i]][ans.citys[i + 1]];cout << "nCase = " << nCase << endl;Print(ans, n);nCase++;return ans;
}void SA(int n)
{double t = T;srand((unsigned)(time(NULL)));Path curPath = bestPath;Path newPath = bestPath;int P_L = 0;int P_F = 0;while(1)       //外循环，主要更新参数t，模拟退火过程
    {for(int i = 0; i < ILOOP; i++)    //内循环，寻找在一定温度下的最优值
        {newPath = GetNext(curPath, n);double dE = newPath.len - curPath.len;if(dE < 0)   //如果找到更优值，直接更新
            {curPath = newPath;P_L = 0;P_F = 0;}else{double rd = rand() / (RAND_MAX + 1.0);//如果找到比当前更差的解，以一定概率接受该解，并且这个概率会越来越小if(exp(dE / t) > rd && exp(dE / t) < 1)curPath = newPath;P_L++;}if(P_L > LIMIT){P_F++;break;}}if(curPath.len < bestPath.len)bestPath = curPath;if(P_F > OLOOP || t < EPS)break;t *= DELTA;}
}int main(int argc, const char * argv[]) {freopen("TSP.data", "r", stdin);int n;Input(p, n);GetDist(p, n);Init(n);SA(n);Print(bestPath, n);printf("Total test times is : %d\n", nCase);return 0;
}

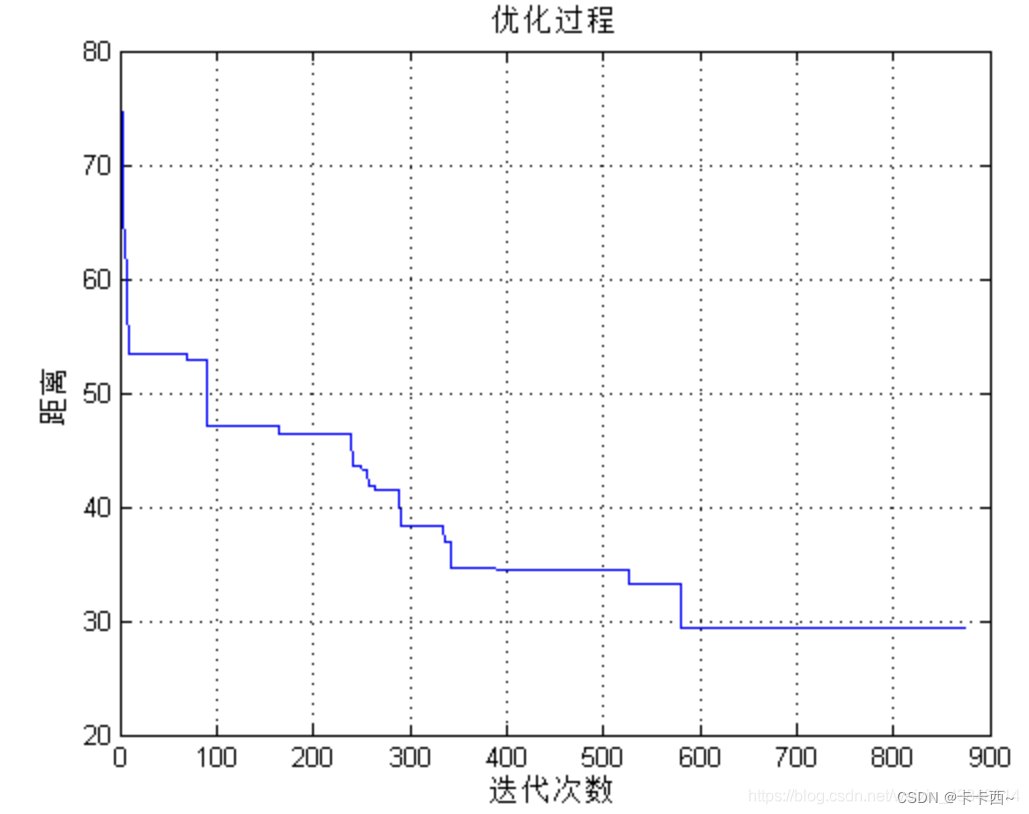
注意由于是基于蒙特卡洛的方法，所以上面代码每次得出的结果并不完全一致。你可以通过增加迭代的次数来获得一个更优的结果。

我们这里需要说明的是，在之前的文章里，我们用求最小值的例子来解释模拟退火的执行：如果新一轮的计算结果更前一轮之结果更小，那么我们就接受它，否则就以一个概率来拒绝或接受它，而这个拒绝的概率会随着温度的降低（也即是迭代次数的增加）而变大（也就是接受的概率会越来越小）。

但现在我们面对一个TSP问题，我们如何定义或者说如何获取下一轮将要被考察的哈密尔顿路径呢？在一元函数最小值的例子中，下一轮就是指向左或者向右移动一小段距离。而在TSP问题中，我们可以采用的方式其实是很多的。上面代码中GetNext()函数所采用的方式是随机交换两个城市在路径中的顺序。例如当前路径为 A->B->C->D->A，那么下一次路径就可能是A->D->C->B->A，即交换B和D。而在文献【3】中，作者采样的代码如下（我们截取一个片段，完整代码请参考原文）：

public class Tour{... ...// Creates a random individual public void generateIndividual() { // Loop through all our destination cities and add them to our tour for (int cityIndex = 0; cityIndex < TourManager.numberOfCities(); cityIndex++) { setCity(cityIndex, TourManager.getCity(cityIndex)); } // Randomly reorder the tour Collections.shuffle(tour); } ... ... }

可见作者的方法是把上一轮路径做一个随机的重排（这显然也是一种策略）。

TSP.data的数据格式如下，第一行的数字表示一个有多少座城市，第2至最后一行，每行有两个数字表示，城市的坐标（平面直角坐标系）。例如：
6
20 80
16 84
23 66
62 90
11 9
35 28
最后请读者自行编译执行程序并观察分析输出的结果。