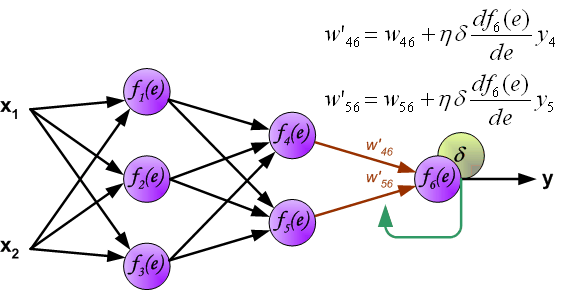
一、概述

本文的推导参见西瓜书P102~P103，代码参见该网址。主要实现了利用三层神经网络进行手写数字的识别。

二、理论推导

1、参数定义

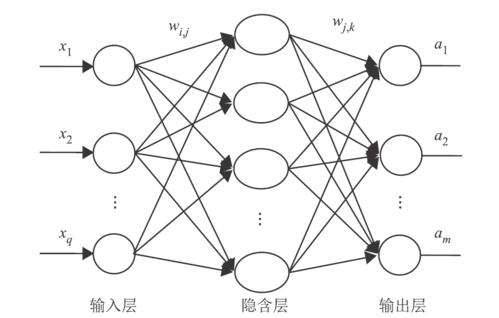
三层神经网络只有一层隐藏层。参数如下：

x	输入层输入
v	输入层与隐藏层间的权值
α	隐藏层输入
b	隐藏层输出
w	隐藏层与输出层间的权值
$\beta$	输出层输入
$\hat y$	输出层输出

参数关系如下：

$\alpha_h= \sum_{i=1}^{d}{v_{ih}x_i}$

$b_h=f(\alpha_h)$

$\beta_j=\sum^{q}_{h=1}{w_{hj}b_h}$

$\hat y=f(\beta_j)$

上述等式中fx为激活函数。西瓜书默认激活函数为sigmoid，损失函数为均方根，本文以此为前提进行推导。

2、推导

设损失函数为 $E$ ，则其公式如下：

$E=\frac{1}{2}\sum^{l}_{j=1}({y_j-\hat y_j})^2$

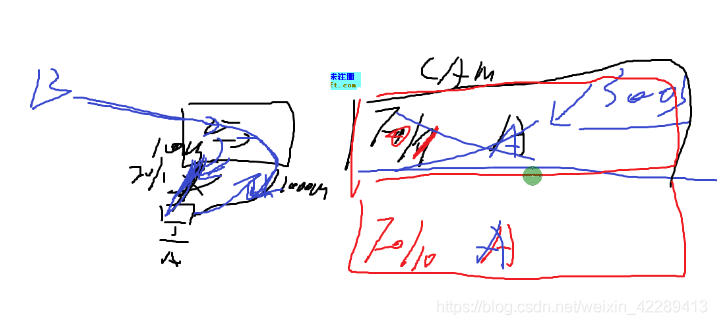
对 $w_{hj}$ 求偏导如下，这愚蠢的CSDN不支持多行公式编辑，所以只好手写了：

于是我们就得到了 $w_{hj}$ 的更新公式：

$\Delta w_{hj}=\eta(y_j-\hat y_j)\hat y_j(1-\hat y_j)b_h$

同样的，对 $v_{ih}$ 求偏导如下：

于是我们就得到了 $v_{ih}$ 的更新公式：

$\Delta v_{ih}=\eta x_i b_h(1-b_h)\sum^l_{j=1}((y_j-\hat y_j)\hat y_j(1-\hat y_j)w_{hj})$

三、代码实现

优化方法选择SGD。

1、数据集初始化

MNIST数据集可以在TensorFlow中下载到：

import tensorflow.examples.tutorials.mnist.input_data as input_data
mnist = input_data.read_data_sets("./MNIST_data/", one_hot=True)

mnist对象中就存储着所有的数据，其中，mnist.train.images为50000*784的二维array；储存着训练集的输入，每一行储存着784个像素；mnist.train.labels为50000*10的二维array；储存着训练集的标记，每一行中为1的列对应着该行的label。

2、初始化神经网络类

class NeuralNet:def __init__(self,InputNum,HiddenNum,OutputNum,LearnRate):self.InNum=InputNum#输入层节点数self.HiNum=HiddenNum#隐藏层节点数self.OuNum=OutputNum#输出层节点数self.LeRate=LearnRate#学习率self.MatrixInputHidden=np.random.normal(0.0,pow(self.HiNum,-0.5),(self.HiNum,self.InNum))#输入层和隐藏层之间的矩阵,100*784self.MatrixHiddenOutput=np.random.normal(0.0,pow(self.OuNum,-0.5),(self.OuNum,self.HiNum))#隐藏层和输出层之间的矩阵,10*100self.activation_function=lambda x:1/(1+np.exp(-x))

由1可知，输入层节点数为784，隐藏层节点数暂定为100，输出层节点数为10，学习率暂定为10。

则输入层和隐藏层之间的系数矩阵MatrixInputHidden应该是一个100*784的矩阵。隐藏层和输出层之间的系数矩阵MatrixHiddenOutput应该是一个10*100的矩阵。将其初始化为均值为0的正态分布。

3、训练函数：

def train(self,TrainData,TargetData):#784*1;10*1HiddenZ=self.activation_function(np.dot(self.MatrixInputHidden,TrainData))#TrainData中，每列是一个样本,HiddenZ中，每列是一个样本的隐藏层输出OutputZ=self.activation_function(np.dot(self.MatrixHiddenOutput,HiddenZ))#OutputZ中，每列是一个样本的输出层输出ErrorOutput=TargetData-OutputZ#输出层误差ErrorHidden=np.dot(self.MatrixHiddenOutput.T,ErrorOutput)#隐藏层误差DeltaMatrixHiddenOutput=self.LeRate*np.dot((ErrorOutput*OutputZ*(1-OutputZ))[:, None],HiddenZ[None,:])DeltaMatrixInputHidden=self.LeRate*np.dot((ErrorHidden*HiddenZ*(1-HiddenZ))[:, None],TrainData[None,:])self.MatrixHiddenOutput+=DeltaMatrixHiddenOutputself.MatrixInputHidden+=DeltaMatrixInputHidden

训练函数的功能是参数优化。

输入一个784*1的向量和一个10*1的向量，分别是一个样本的输入和标记，对输入向量进行计算可以得到一个预测向量。通过预测向量和标记的差值可以得到损失值，从而可以对参数进行修改。

这里较难的一点是将如下两个公式矩阵化：

$\Delta w_{hj}=\eta(y_j-\hat y_j)\hat y_j(1-\hat y_j)b_h$

$\Delta v_{ih}=\eta x_i b_h(1-b_h)\sum^l_{j=1}((y_j-\hat y_j)\hat y_j(1-\hat y_j)w_{hj})$

因为参数是以矩阵的形式存储的，所以，对参数的更新也应该以矩阵的形式。也就是说，我们需要计算出 $\Delta w_{hj}$ 矩阵和 $\Delta v_{ih}$ 矩阵。首先计算前者。

$\Delta w_{hj}$ 矩阵应该是一个10*100的矩阵，我们观察公式可知， $y_j$ 对应一个 $y$ 向量， $\hat y_j$ 对应一个 $\hat y$ 向量，都是10*1的向量； $b_h$ 对应b向量，是100*1的向量——所以我们要得到一个10*100的向量，需要用 $y$ 向量乘以b向量的转置，即10*1的向量乘以1*100的向量，即可得到10*100的矩阵。

这对应如下一行代码：

ErrorOutput=TargetData-OutputZ#输出层误差
DeltaMatrixHiddenOutput=self.LeRate*np.dot((ErrorOutput*OutputZ*(1-OutputZ))[:, None],HiddenZ[None,:])

注意，向量在python是没有转置的，将其转置需要用[None,:]来进行。

然后计算后者。

$\Delta v_{ih}$ 矩阵应该是一个100*784的矩阵，我们观察公式可知， $x_i$ 对应一个 $x$ 向量，是784*1的向量； $b_h(1-b_h)$ 是对应元素相乘，是一个100*1的向量； $y_j$ 对应一个 $y$ 向量， $\hat y_j$ 对应一个 $\hat y$ 向量，都是10*1的向量； $w_{hj}$ 对应 $w$ 矩阵，是一个10*100的矩阵。这就有点复杂了——向量乘矩阵，如何安排其顺序才能得到正确的结果呢？

先看累加部分，将其向量化后应该是 $w$ 在前， $y$ 在后；又由于 $w$ 是一个10*100的矩阵，与10*1不能直接相乘，因此要将其转置，结果是一个100*1的向量。

现在化简了一部分，相乘的矩阵减少为三个：x：784*1；b：100*1；求和部分：100*1。

很明显了，要得到一个100*784的矩阵，需要100*1的向量乘以一个1*784的向量。

我们观察这两个公式的向量化，都是一个向量a乘以一个向量b的转置。其中，向量b的转置对应前一层的输出，向量a对应什么不容易看出来。

不如重新写一下上面的公式吧：

$\Delta w_{hj}=\eta b_h\hat y_j(1-\hat y_j)(y_j-\hat y_j)$

$\Delta v_{ih}=\eta x_i b_h(1-b_h)\sum^l_{j=1}((y_j-\hat y_j)\hat y_j(1-\hat y_j)w_{hj})$

上下对应一下：上面的 $b_h$ 对应下面的 $x_i$ ，上面的 $\hat y_j(1-\hat y_j)$ 对应下面的 $b_h(1-b_h)$ ；因为其实际意义相同， $b_h$ 和 $x_i$ 都是前一层的输出， $\hat y_j$ 和 $b_h$ 都是后一层的输出。那么问题来了： $(y_j-\hat y_j)$ 和 $\sum^l_{j=1}((y_j-\hat y_j)\hat y_j(1-\hat y_j)w_{hj})$ 对应，这俩玩意实际意义有什么相同的？

$(y_j-\hat y_j)$ 可以看做是输出层的误差， $\sum^l_{j=1}((y_j-\hat y_j)\hat y_j(1-\hat y_j)w_{hj})$ 也就可以视作是隐藏层的误差。我们将神经网络视为是无方向的——那么将原来的输出层作为输入层，原来的输出误差视作输入，那么这个输入在隐藏层上的输出就可以看做是隐藏层的误差。当然要作为输入还需要一些处理：需要“输入*激活函数的导数*系数”从而得到隐藏层的误差。

这也是反向传播的名字由来，反向传播，传播的就是误差。这对应以下两行代码：

ErrorHidden=np.dot(self.MatrixHiddenOutput.T,ErrorOutput*OutputZ*(1-OutputZ))#隐藏层误差
DeltaMatrixInputHidden=self.LeRate*np.dot((ErrorHidden*HiddenZ*(1-HiddenZ))[:, None],TrainData[None,:])

4、预测函数

预测函数就是神经网络实际使用的时候调用的函数，给一个输入，返回一个输出，实际上就从训练函数里面摘出来两行就好了：

def query(self,TrainData):HiddenZ=self.activation_function(np.dot(self.MatrixInputHidden,TrainData))#TrainData中，每列是一个样本,HiddenZ中，每列是一个样本的隐藏层输出OutputZ=self.activation_function(np.dot(self.MatrixHiddenOutput,HiddenZ))#OutputZ中，每列是一个样本的输出层输出return OutputZ

5、主函数

if __name__ == "__main__":mnist = input_data.read_data_sets("./MNIST_data/", one_hot=True)InputNum=mnist.train.images.shape[1]HiddenNum=100OutputNum=mnist.train.labels.shape[1]LearnRate=0.2epoch=50nn=NeuralNet(InputNum,HiddenNum,OutputNum,LearnRate)accu=[]for e in range(epoch):for i in range(mnist.train.images.shape[0]):nn.train(mnist.train.images[i].T,mnist.train.labels[i].T)print("已训练"+str(e+1)+"次")num=0for i in range(mnist.test.images.shape[0]):res=nn.query(mnist.test.images[i].T)label=np.argmax(res)correct_label=np.argmax(mnist.test.labels[i])if(label==correct_label):num=num+1print("第"+str(e+1)+"次训练后预测正确率为："+str(num/mnist.test.images.shape[0]))accu.append(num/mnist.test.images.shape[0])plt.figure() #创建绘图对象  plt.plot(accu,"b--",linewidth=1) #在当前绘图对象绘图（X轴，Y轴，蓝色虚线，线宽度）  plt.xlabel("epoch") #X轴标签  plt.ylabel("Accuracy")  #Y轴标签  plt.show()

我们先给神经网络初始化——三层节点数、学习率和迭代优化步数，然后进行训练。

由于我们使用了SGD，即Stochastic Gradient Descent，随机梯度下降，每次选择一个样本计算误差，然后进行优化，这样总计50000个样本，一次迭代可以优化50000次。每次输入一个向量即可。

效果如下：

可以看出，在第一次的50000个样本优化之后，总的准确率已经达到了0.9463，在之后准确率不断上升，但上升速度不断变慢。由于SGD并不会每次选择最优的梯度进行优化，因此可能出现准确率变少的情况，但是总体趋势仍是向上的。

四、不同的优化方法对比

在三中，我们选择使用SGD，CostFunction选择使用均方根误差(Quadratic cost)。接下来我们将选择batch GD、mini batchGD进行优化。同时选择交叉熵函数(Cross-entropy cost)作为对比。

1、SGD改为batchGD

这俩优化方法的区别很明显：

SGD是选择一个样本，求误差，对这个误差求偏导，更新参数；batchGD则是选择所有样本，求误差和，对误差和求偏导，然后除以总的样本数量，更新参数。更改后的train函数代码如下：

def train(self,TrainData,TargetData):#784*50000;10*50000；Batch GDHiddenZ=self.activation_function(np.dot(self.MatrixInputHidden,TrainData))#100*50000OutputZ=self.activation_function(np.dot(self.MatrixHiddenOutput,HiddenZ))#10*50000ErrorOutput=TargetData-OutputZ#输出层误差,10*50000ErrorHidden=np.dot(self.MatrixHiddenOutput.T,ErrorOutput*OutputZ*(1-OutputZ))#隐藏层误差,100*50000DeltaMatrixHiddenOutput=self.LeRate*(np.dot((ErrorOutput*OutputZ*(1-OutputZ)),HiddenZ.T)/TrainData.shape[1])DeltaMatrixInputHidden=self.LeRate*(np.dot((ErrorHidden*HiddenZ*(1-HiddenZ)),TrainData.T)/TrainData.shape[1])self.MatrixHiddenOutput+=DeltaMatrixHiddenOutputself.MatrixInputHidden+=DeltaMatrixInputHidden

主函数调用如下：

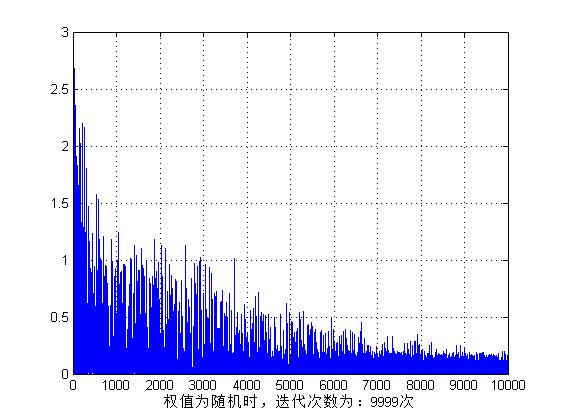
if __name__ == "__main__":mnist = input_data.read_data_sets("./MNIST_data/", one_hot=True)InputNum=mnist.train.images.shape[1]HiddenNum=100OutputNum=mnist.train.labels.shape[1]LearnRate=0.2epoch=500nn=NeuralNet(InputNum,HiddenNum,OutputNum,LearnRate)accu=[]for e in range(epoch):nn.train(mnist.train.images.T,mnist.train.labels.T)print("已训练"+str(e+1)+"次")num=0for i in range(mnist.test.images.shape[0]):res=nn.query(mnist.test.images[i].T)label=np.argmax(res)correct_label=np.argmax(mnist.test.labels[i])if(label==correct_label):num=num+1print("第"+str(e+1)+"次训练后预测正确率为："+str(num/mnist.test.images.shape[0]))accu.append(num/mnist.test.images.shape[0])plt.figure() #创建绘图对象  plt.plot(accu,"b--",linewidth=1) #在当前绘图对象绘图（X轴，Y轴，蓝色虚线，线宽度）  plt.xlabel("epoch") #X轴标签  plt.ylabel("Accuracy")  #Y轴标签  plt.show()

效果如下：

由此，batchGD和SGD的区别在于：batchGD每次迭代的方向都是对的，就是幅度可能有区别；SGD的方向可能错误，幅度也有区别。由于用的是我自己的小破电脑跑的，因此只迭代了五百次，最终准确率为85.64%。与SGD的97.7%还有较大差距。但是想到SGD即使只迭代一次也优化了50000次，而batchGD只优化了500次，这个准确率也是可以接受的。

2、SGD改为mini batch GD

mini batch GD和batchGD使用的train函数是一样的，只不过是每次训练使用的样本数量不同，后者使用所有50000个样本，前者我选择使用50个样本。调用函数如下：

if __name__ == "__main__":mnist = input_data.read_data_sets("./MNIST_data/", one_hot=True)InputNum=mnist.train.images.shape[1]HiddenNum=100OutputNum=mnist.train.labels.shape[1]LearnRate=0.2epoch=100nn=NeuralNet(InputNum,HiddenNum,OutputNum,LearnRate)accu=[]for e in range(epoch):for i in range(0,mnist.train.images.shape[0],50):nn.train(mnist.train.images[i:i+50].T,mnist.train.labels[i:i+50].T)print("已训练"+str(e+1)+"次")num=0for i in range(mnist.test.images.shape[0]):res=nn.query(mnist.test.images[i].T)label=np.argmax(res)correct_label=np.argmax(mnist.test.labels[i])if(label==correct_label):num=num+1print("第"+str(e+1)+"次训练后预测正确率为："+str(num/mnist.test.images.shape[0]))accu.append(num/mnist.test.images.shape[0])plt.figure() #创建绘图对象  plt.plot(accu,"b--",linewidth=1) #在当前绘图对象绘图（X轴，Y轴，蓝色虚线，线宽度）  plt.xlabel("epoch") #X轴标签  plt.ylabel("Accuracy")  #Y轴标签  plt.show()

效果如下：

效果好的出奇——没有方向相反的情况，一直是增加，而且仅100次优化离SGD的最佳值差距已很小。我不禁怀疑我的batchGD是不是写错了。这被另外俩完爆。你说这个batchGD，它用内存有多，计算又慢，唯一的优点是收敛稳定，这优点人家minibatchGD也有，还比你用内存少，还比你快。人比人气死人。

五、不同的CostFunction对比

这里我们选择使用Cross-entropy cost，对于多分类问题，其公式如下：

$E=-\frac{1}{n}\sum_{x}\sum_{j}({y_jln\hat y_j}+(1-y_j)ln(1-\hat y_j))^2$

对 $w_{hj}$ 求偏导如下：

于是我们可以得到更新的公式如下：

$\Delta w_{hj}=-\eta(y_j-\hat y_j)b_h$

同理，对 $v_{ih}$ 求偏导如下：

于是我们可以得到更新公式如下：

$\Delta v_{ih}=-\eta x_i b_h(1-b_h)\sum^l_{j=1}((y_j-\hat y_j)w_{hj})$

可以看出，交叉熵函数就是比均方根函数少了一个系数罢了。因此train函数也很容易更改：

def train(self,TrainData,TargetData):#784*1;10*1；SGD;CrossEntropyHiddenZ=self.activation_function(np.dot(self.MatrixInputHidden,TrainData))#TrainData中，每列是一个样本,HiddenZ中，每列是一个样本的隐藏层输出OutputZ=self.activation_function(np.dot(self.MatrixHiddenOutput,HiddenZ))#OutputZ中，每列是一个样本的输出层输出ErrorOutput=TargetData-OutputZ#输出层误差ErrorHidden=np.dot(self.MatrixHiddenOutput.T,ErrorOutput)#隐藏层误差DeltaMatrixHiddenOutput=self.LeRate*np.dot((ErrorOutput)[:, None],HiddenZ[None,:])DeltaMatrixInputHidden=self.LeRate*np.dot((ErrorHidden*HiddenZ*(1-HiddenZ))[:, None],TrainData[None,:])self.MatrixHiddenOutput+=DeltaMatrixHiddenOutputself.MatrixInputHidden+=DeltaMatrixInputHidden

效果如下：