三层神经网络的BP（BackPropagation）算法推导

article/2025/8/23 23:27:03

BP算法：

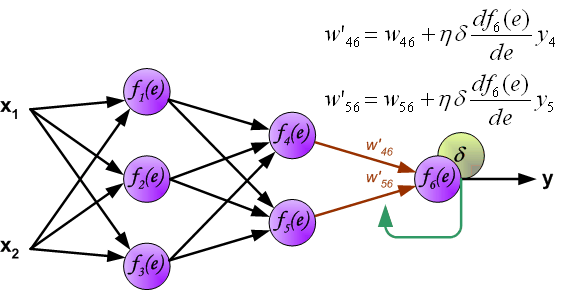
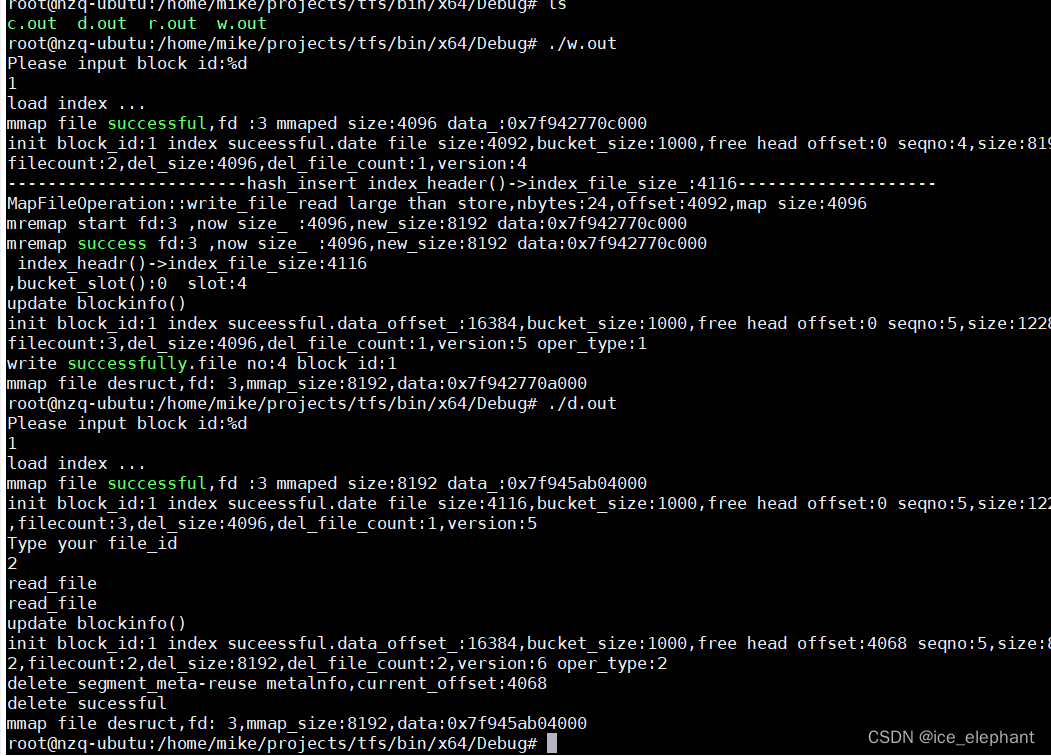
利用的是sigmoid函数来搭建的一个三层神经网络。假设其拓扑结构如图1-1所示。

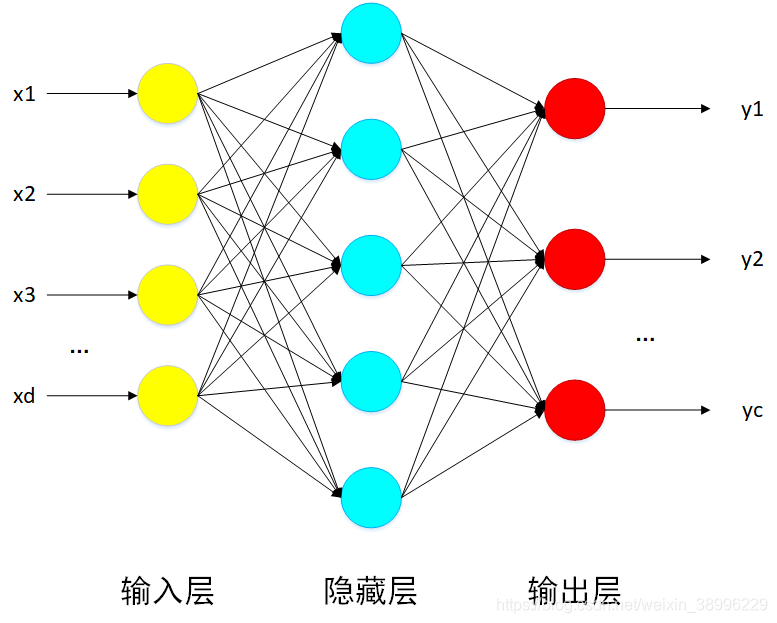
该网络的运行流程为：当输入一个样例后，获得该样例的特征向量，再根据权向量得到感知机的输入值，然后使用sigmoid函数计算出每个感知机的输出，再将输出作为下一层感知机的输入，以此类推，知道输出层。

反向传播算法就是用来对每个感知机的权向量逐步进行优化。为了得到最优化权向量，这边我们使用L2作为损失函数来不断调整权向量。下面就是每一个训练样例的损失函数（式1-1）：

$E(\overrightarrow{\omega })=\frac{1}{2}_{k\epsilon outputs}\sum(t_{k}-o_{k})^{2}$ (式1-1)

在多层神经网络中，误差曲面可能有多个局部极小值，所以我们用梯度下降找到的是局部极小值，而不是全局最小值。

具有一层隐藏层的反向传播：

1.将网络中的所有权值随机初始化。

2.对每一个训练样例，执行如下操作：

A.根据实例的输入，从前往后依次计算，得到输出层的每个单元的输出。然后从输出层开始反向计算每一层的每个单元的误差。

B.对于输出层的每个单元的k,计算它的误差：

$\delta _{k} = O_{k}(1-O_{k})(t_{k}-O_{k}])$ (式1-2)

C.对于网络中每个隐藏层单元h,计算他的误差项：

$\delta _{h} = O_{h}(1-O_{h})\sum_{k\in outputs}w_{kh}\delta_{h}$ (式1-3)

D.更新每个权值：

$w_{ji} = w_{ji} + \eta \delta_{j}x_{ji}$ （式1-4）

$\bigtriangleup w_{ji} = \eta\delta_{j}x_{ji}$ 被称为权值更新法则 (式1-5)

符号说明：

$x_{ji}$ :节点i到节点j的输入， $w_{ji}$ :表示节点i到节点j对应的权值

outputs:表示整个输出层结点集合

BP算法推导过程：

算法的推导主要是利用梯度下降算法求解最小化损失函数的过程，现在损失函数为：

$E(\overrightarrow{\omega })=\frac{1}{2}_{k\epsilon outputs}\sum(t_{k}-o_{k})^{2}$

对于网络中每个权值 $w_{ji}$ ,计算其导数：

$\frac{\partial E}{\partial w_{ji}} = \frac{\partial E}{\partial net_{j}} \frac{\partial net_{j}}{\partial w_{ji}}$

$= \frac{\partial E}{\partial net_{j}} \frac{\partial}{\partial w_{ji}}(\sum_{i=0}^{n}w_{ji}x_{ji})$

$= \frac{\partial E}{\partial net_{j}} x_{ji}$

1.若j是网络层的输出单元

对 $net_{j}$ 的求导：

$\frac{\partial E}{\partial net_{j}} = \frac{\partial E}{\partial O_{j}} \frac{\partial O_{j}}{\partial net_{j}}$

其中：

$\frac{\partial E}{\partial O_{j}}= \frac{\partial}{\partial O_{j}} \sum_{k\in outputs }(t_{k} - O_{k}) ^{2}$

$\overset{k=j}{=}\frac{1}{2}2(t_{j} - O_{j})\frac{\partial (t_{j} - O_{j})) }{\partial O_{j}}$

$= -(t_{j} - O_{j})$

$\frac{\partial O_{j}}{\partial net_{j}} = \frac{\partial \sigma(net_{j})}{\partial net_{j}} = O_{j}(1 - O_{j})$

所以有：

$\frac{\partial E}{\partial net_{j}} = \frac{\partial E}{\partial O_{j}} \frac{\partial O_{j}}{\partial net_{j}}$

$= -(t_{j} - O_{j})O_{j}(1-O_{j})$

为了使表达简洁，我们使用：

$\delta _{i} = - \frac{\partial E}{\partial net_{j}} = (t_{j} - O_{j})O_{j}(1-O_{j})$

权值的改变朝着损失函数的负梯度方向，于是有权值改变量：

$\bigtriangleup w_{ji} = -\eta \frac{\partial E }{\partial w_{ji}}$

$= -\eta[-(t_{j} - O_{j})O_{j}(1-O_{j})]x_{ji} = \eta(t_{j} - O_{j})O_{j}(1-O_{j})x_{ji}=\eta\delta _{j}x_{ji}$

2.若j是网络层的隐藏单元

由于隐藏单元中w的值通过下一层来间接影响输入，故使用剥离的方式来进行求导：

$\frac{\partial E}{\partial net_{j}}$ $= \sum_{k \in outputs} \frac{\partial E}{\partial net_{k}} \frac{\partial net_{k}}{\partial net_{j}}$ $= \sum_{k \in outputs} -\delta_{k} \frac{\partial net_{k}}{\partial net_{j}}$ $= \sum_{k \in outputs} -\delta_{k} \frac{\partial net_{k}}{\partial \sigma _{j}} \frac{\partial \sigma_{j}}{\partial net_{j}}$

因为：

$\frac{\partial net_{k}}{\partial \sigma_{j}}$ $= \frac{\partial }{\partial net_{j}}\sum _{s \in hidenlayer}w_{ks}\sigma_{ks} = w_{kj}$

$\frac{\partial \sigma_{j}}{\partial net_{j}} = O_{j}(1-O_{j})$

所以：

$\sum_{k \in outputs} -\delta_{k} \frac{\partial net_{k}}{\partial \sigma _{j}} \frac{\partial \sigma_{j}}{\partial net_{j}}$ $= \sum_{k \in outputs}-\delta_{k}w_{kj}O_{j}(1-O_{j})$