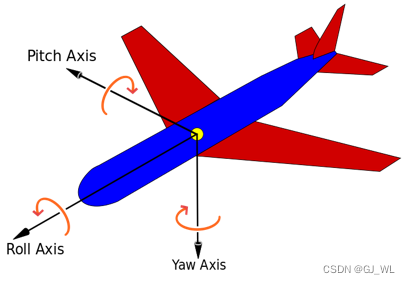
先说明unity 3D欧拉角的旋转顺序(父子关系)是y-x-z。即旋转y轴x和z轴都变,旋转x轴只有z轴变化,旋转z轴其它轴不变。
模型坐标系
又称物体坐标系。
与特定的物体关联,每个物体都有自己特定的坐标系。不同物体之间的坐标系相互独立,可以相同,可以不同,没有任何联系。同时,物体坐标系与物体绑定,绑定的意思就是物体发生移动或者旋转,物体坐标系发生相同的平移或者旋转,物体坐标系和物体之间运动同步,相互绑定。
世界坐标系
是一个特殊的坐标系,它建立了描述其他坐标系所需要的参考系。也就是说,可以用世界坐标系去描述其他所有坐标系或者物体的位置。所以有很多人定义世界坐标系是“我们所关心的最大坐标系”,通过这个坐标系可以去描述和刻画所有想刻画的实体。
惯性坐标系
是为了简化世界坐标系到物体坐标系的转化而产生的。惯性坐标系的原点与物体坐标系的原点重合,惯性坐标系的轴平行于世界坐标系的轴。引入了惯性坐标系之后,物体坐标系转换到惯性坐标系只需旋转,从惯性坐标系转换到世界坐标系只需平移。
坐标系之间的联系
下图展示了三个坐标系之间的关系。在机器人的物体坐标系中,y轴从脚指向头而x轴指向它的左边。绕物体坐标系的原点进行旋转。知道物体坐标系的轴与世界坐标系平行就得到了惯性坐标系。最后,把惯性坐标系的原点平移到世界坐标系的原点就完成了惯性坐标系到世界坐标系的转换。
unity模型坐标系和惯性坐标系间的查看方法

local为模型坐标系

global为惯性坐标系
如果你不旋转模型,此时惯性坐标系和模型坐标系重合,你可以点选上面按钮切换看一下。
编写脚本辅助类,显示惯性坐标系的辅助线。
using UnityEngine;public class GizmozHelper : MonoBehaviour
{public float Length = 3;void OnDrawGizmos(){Gizmos.color = Color.red;Vector3 direction = Vector3.right * Length; //世界坐标系的 轴向xGizmos.DrawRay(transform.position, direction);Gizmos.color = Color.green;direction = Vector3.up * Length; //世界坐标系的 轴向yGizmos.DrawRay(transform.position, direction);Gizmos.color = Color.blue;direction = Vector3.forward * Length; //世界坐标系的 轴向zGizmos.DrawRay(transform.position, direction);}
}
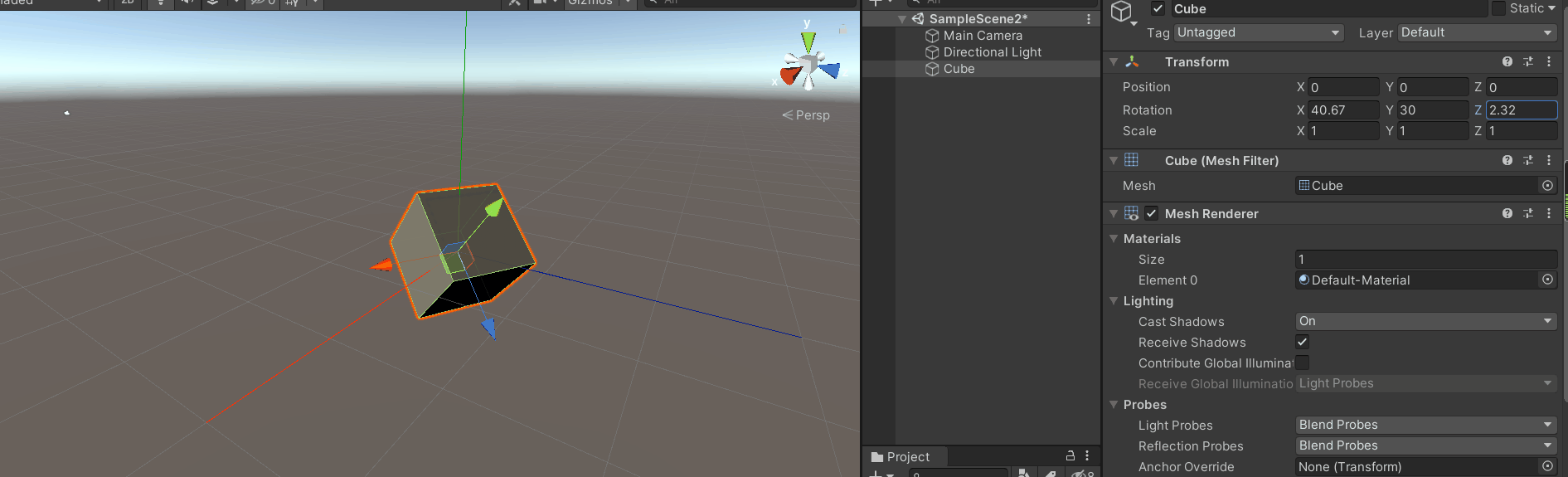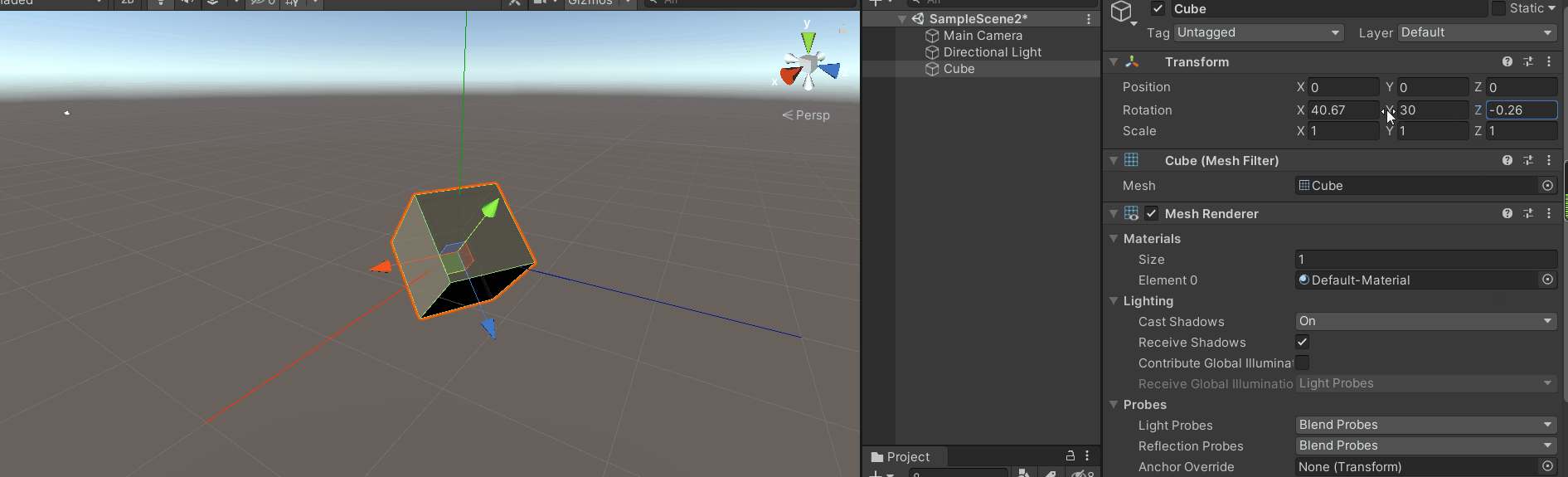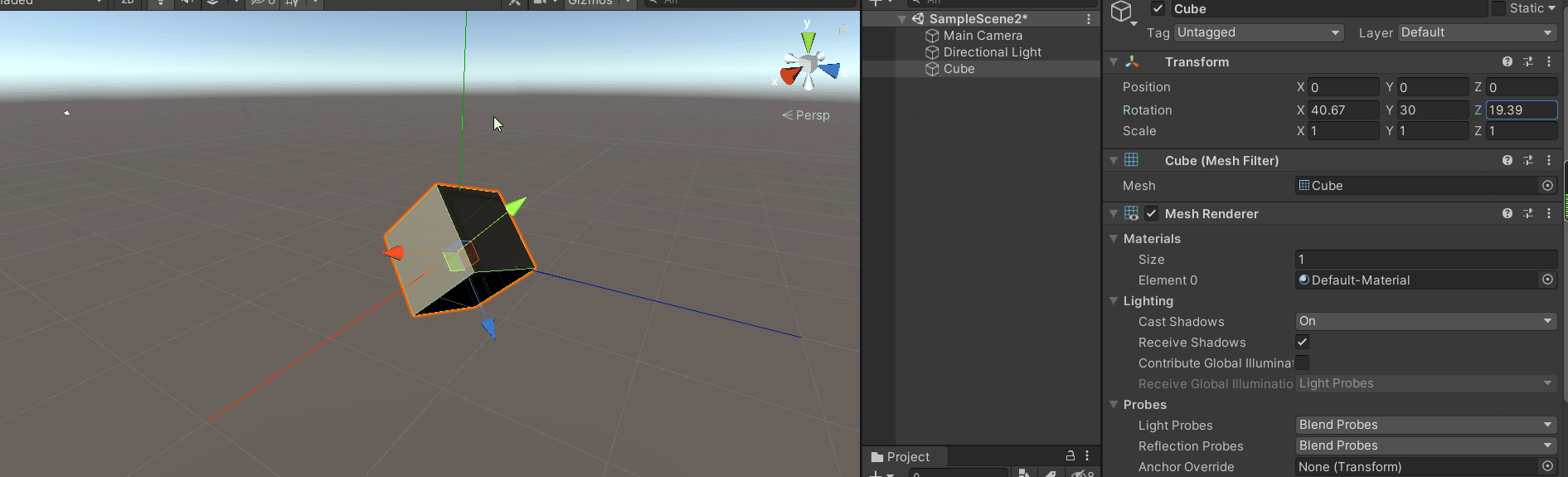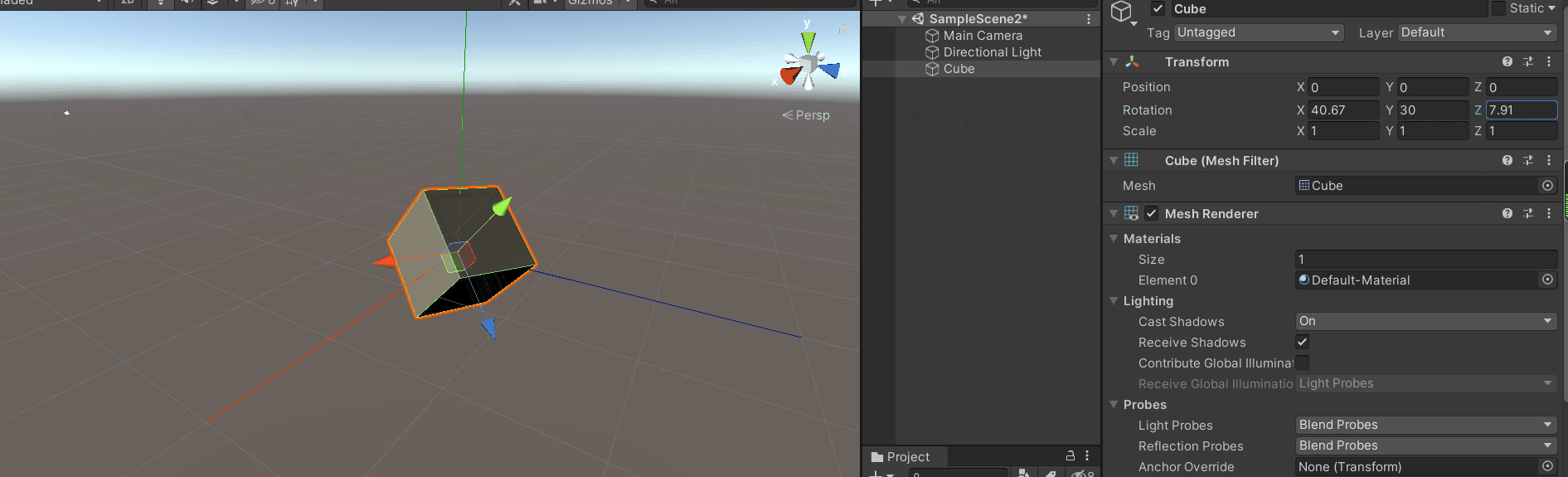
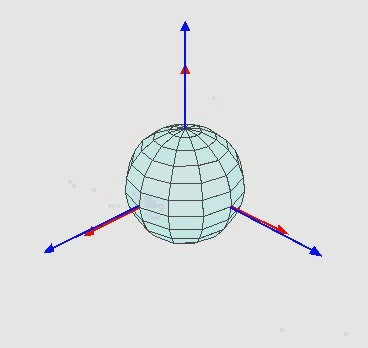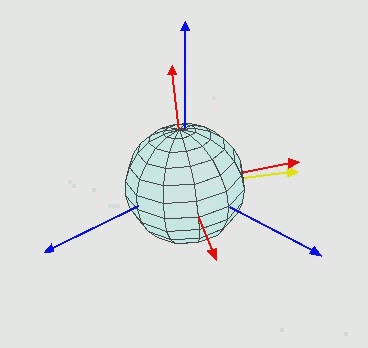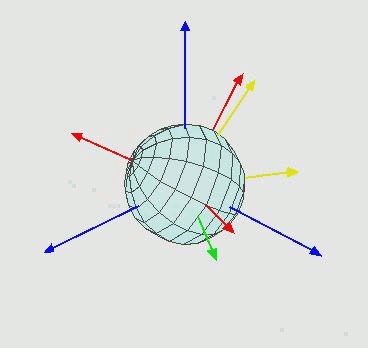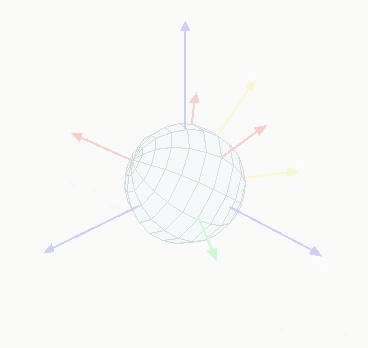
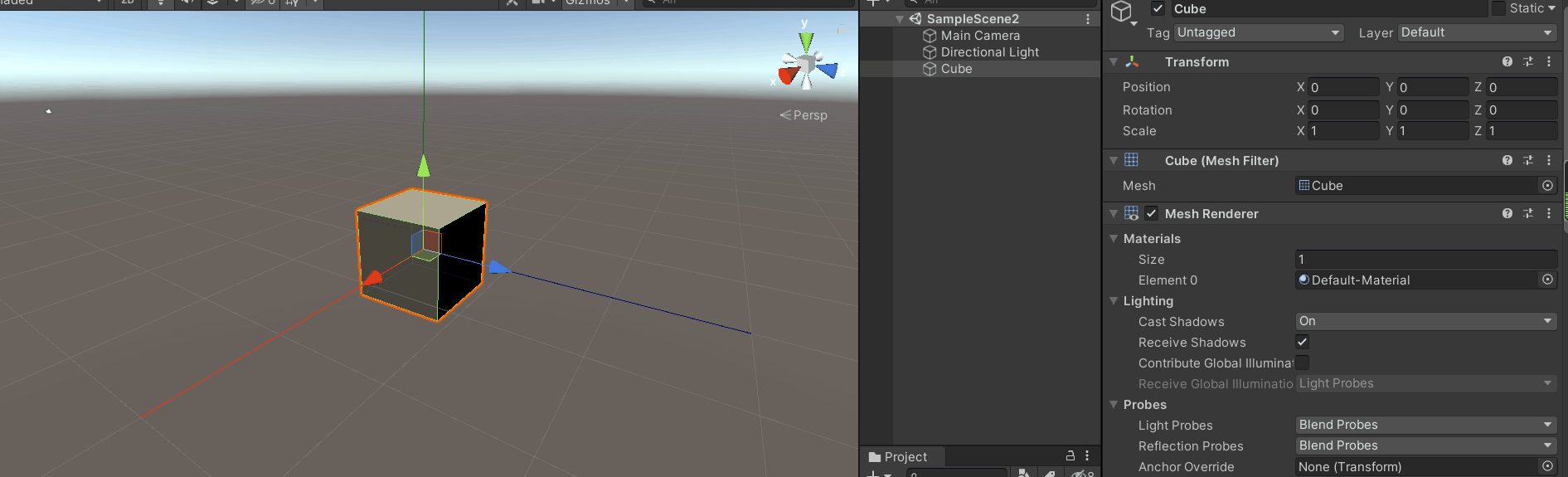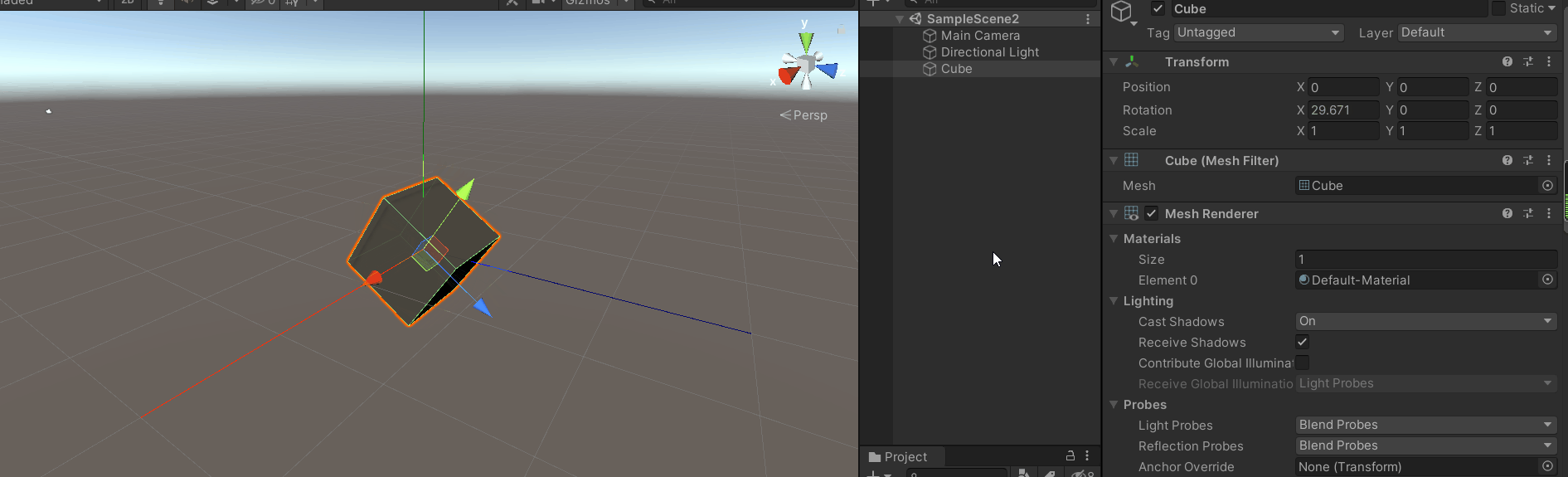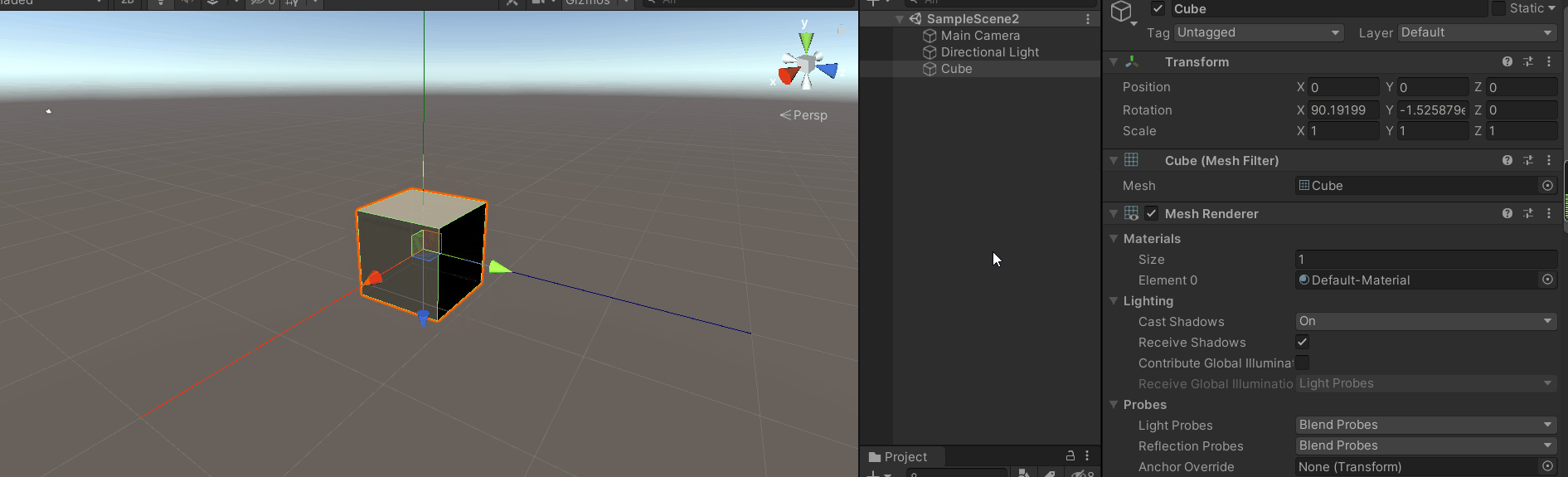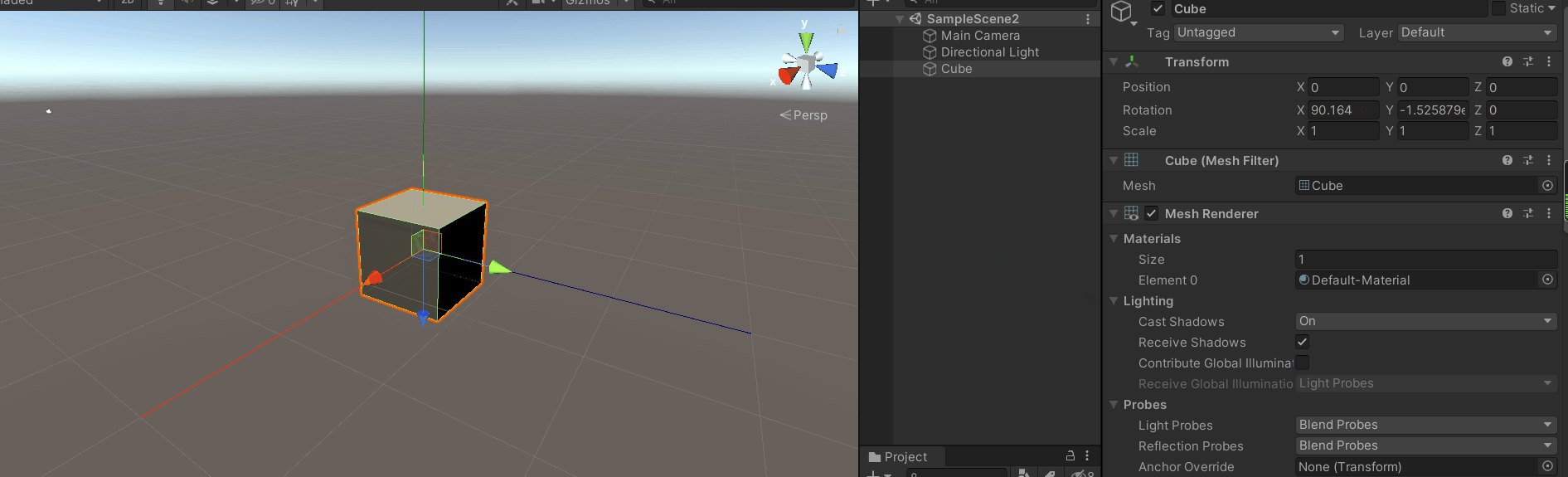
首先将坐标切换到模型坐标,

开始旋转最顶层的y轴。
效果如下图:
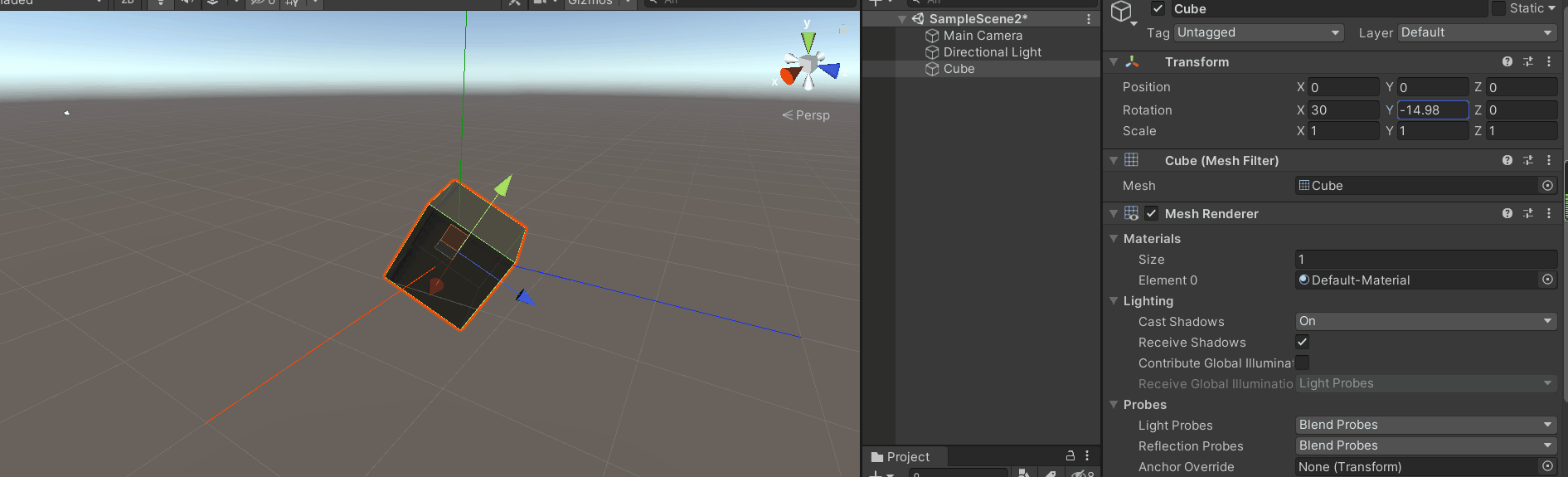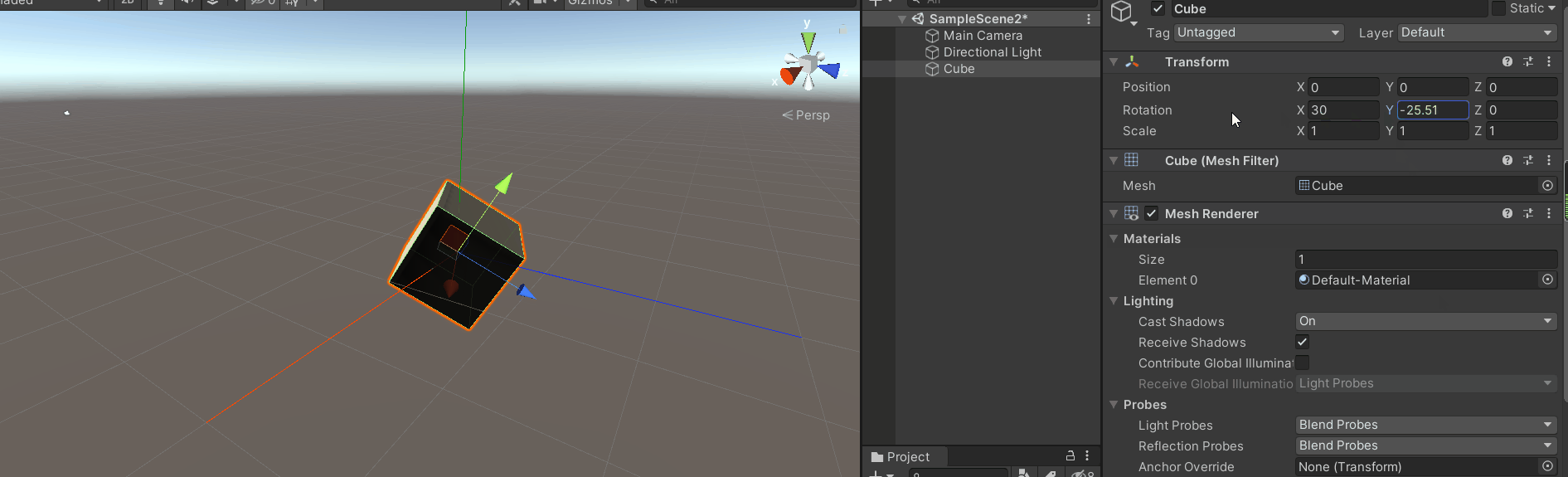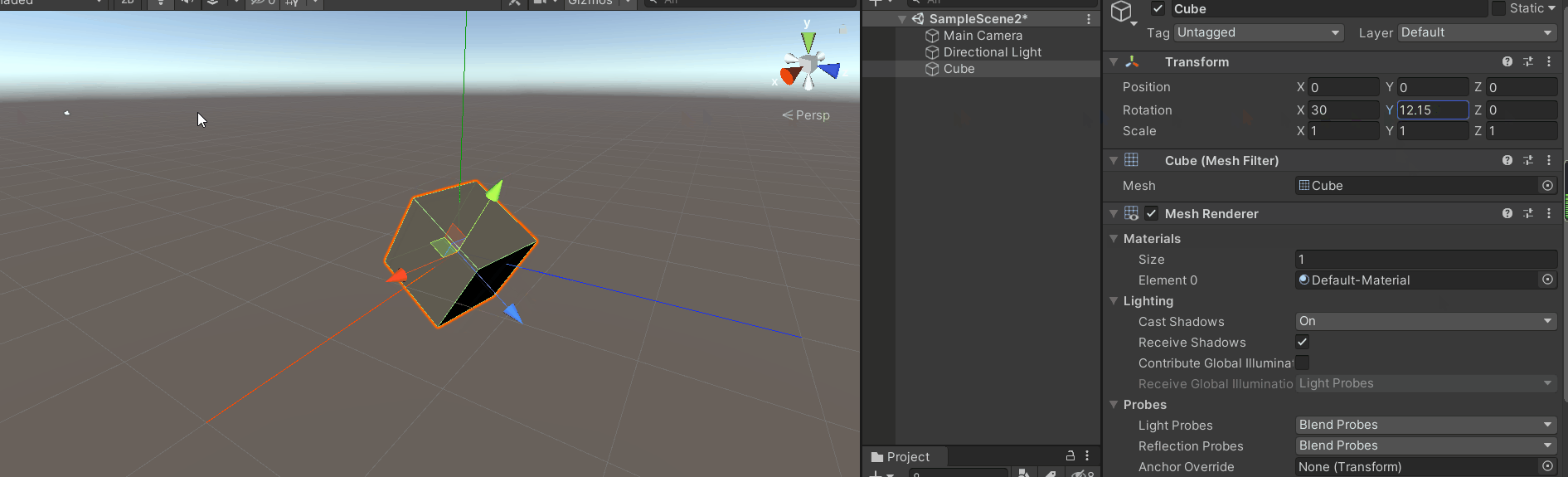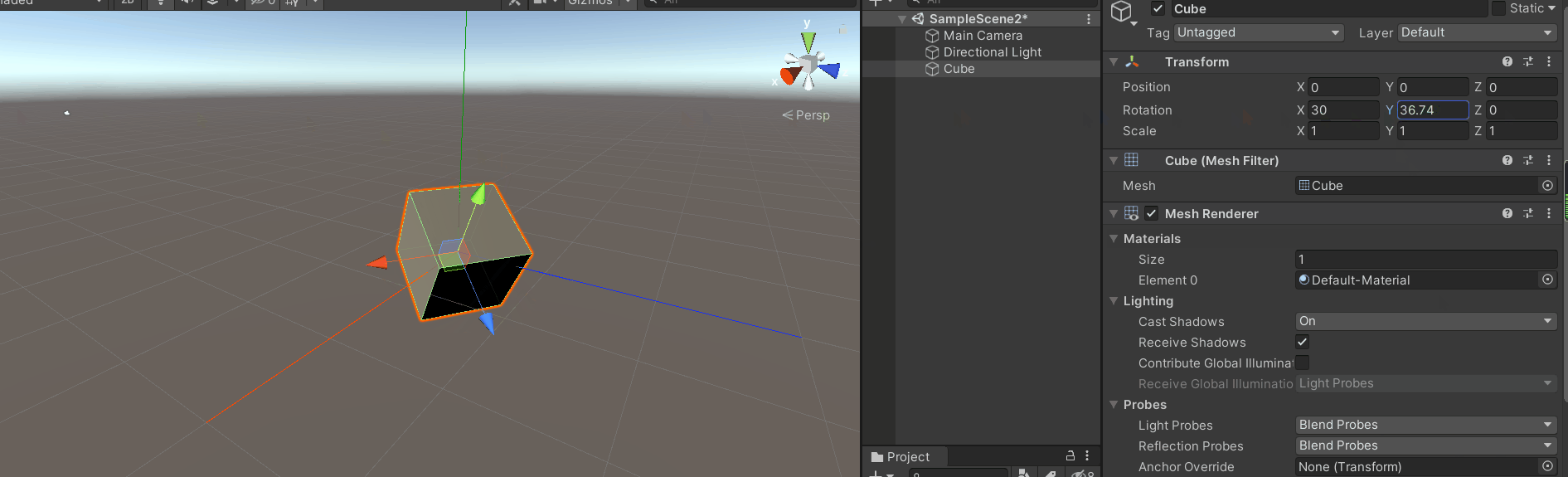
会发现旋转y轴是绕着惯性坐标的y轴旋转的,而不是模型的坐标。
旋转x轴,会发现x轴的变换是绕着模型坐标的x轴进行变换的。
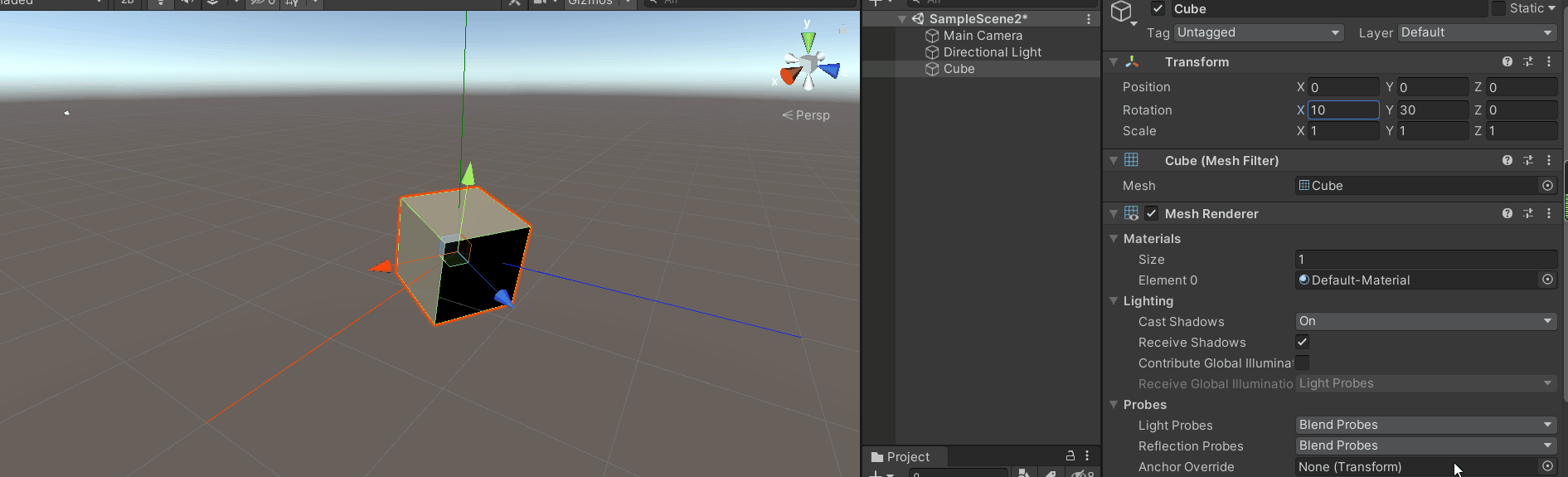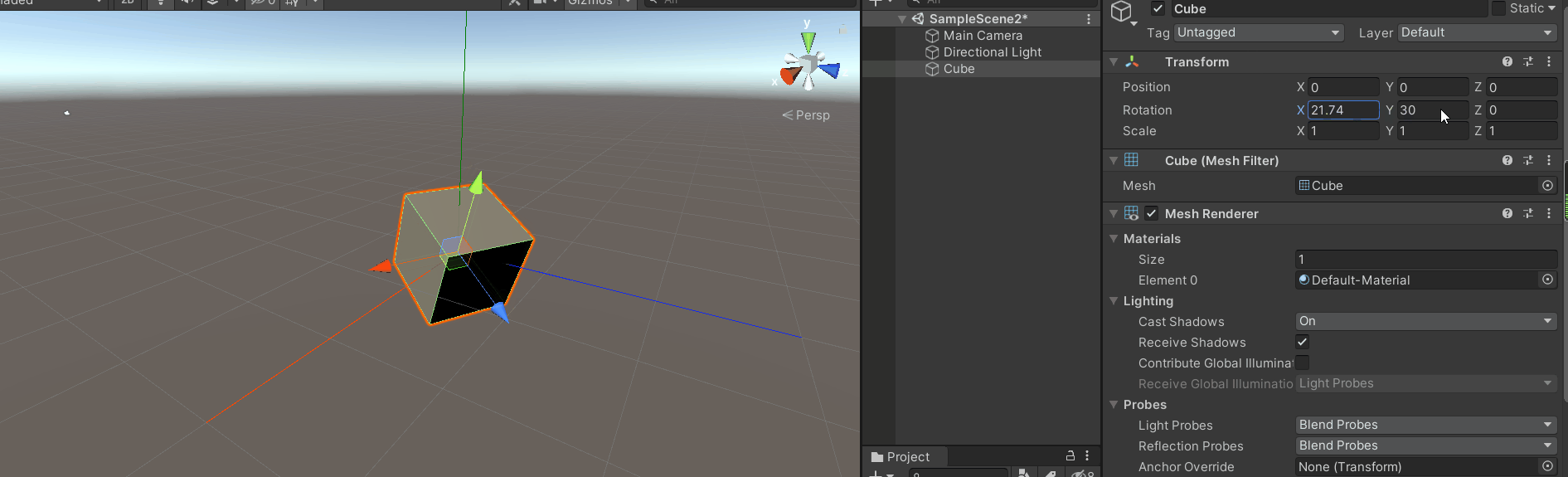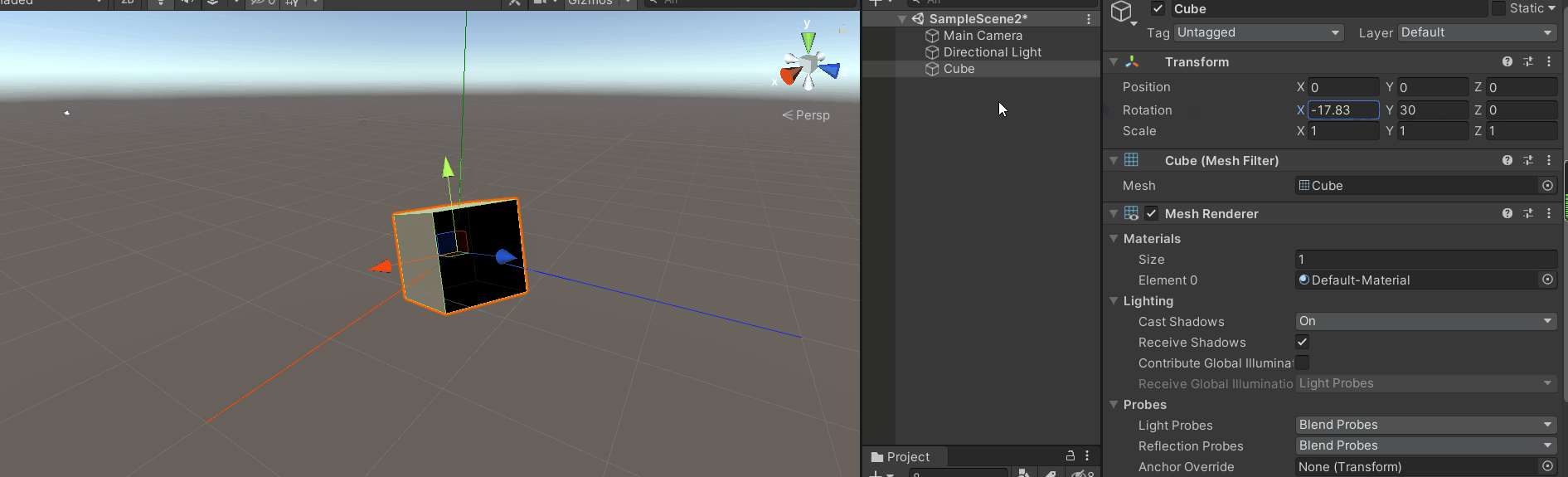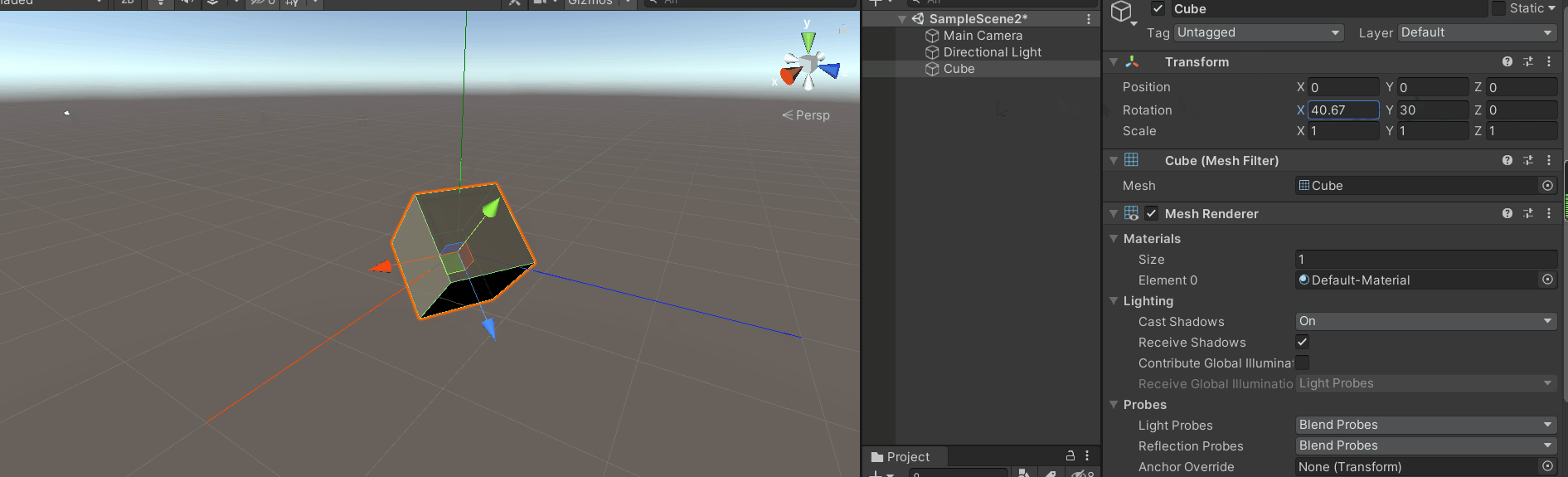
旋转z轴,会发现z轴的变换也是绕着模型的z轴变换。
万向锁(Gimbal lock)
一旦选择±90°作为pitch(俯仰变换)角,就会导致第一次旋转和第三次旋转等价,整个旋转表示系统被限制在只能绕竖直轴旋转,丢失了一个表示维度。
为什么会共面,因为y轴变换将影响x和z轴,因为有轴处在变换的最顶层(y-x-z),最主要的是y轴变换是模型在惯性坐标里变换,而其他轴的变换是在模型轴变换。所以就会出旋转面共面(万向锁)的情况。
下面开始说明万向锁的情况。
将模型x轴旋转90度(或者-90度)(最简单的万向锁)
紧接着旋转y轴或者z轴,效果如下:
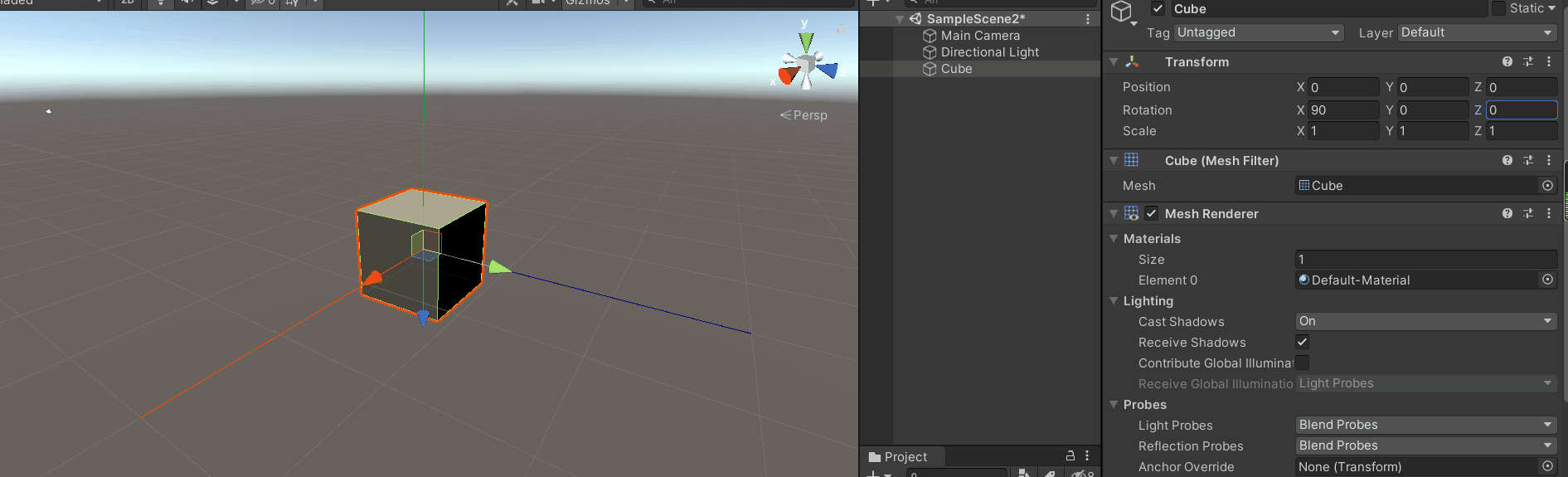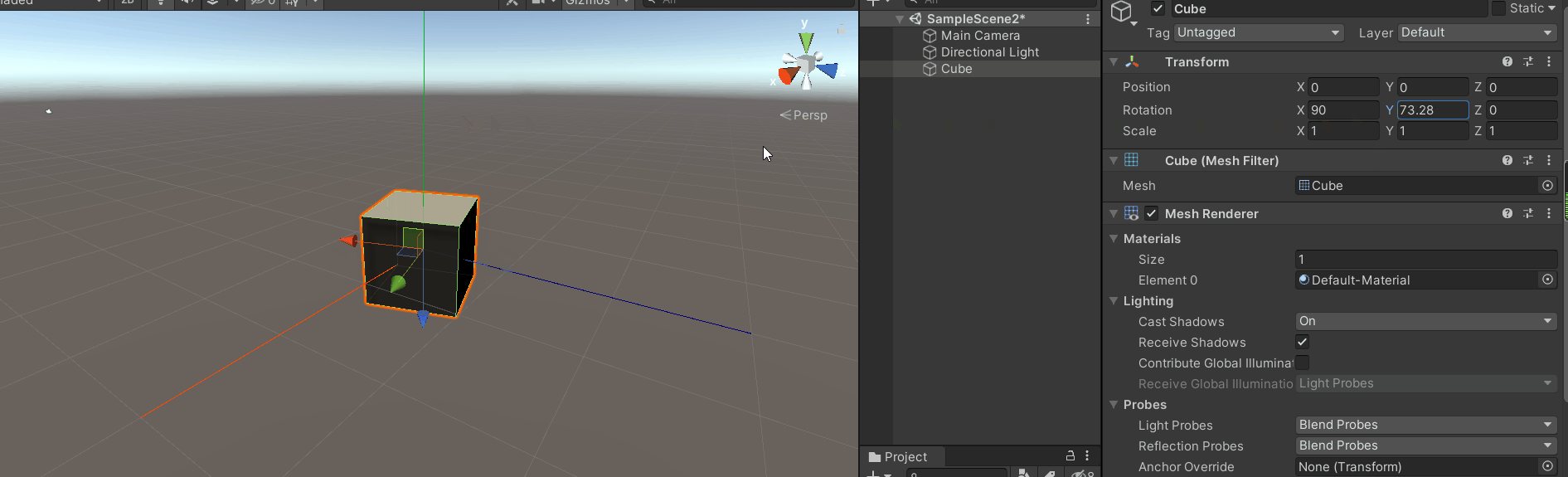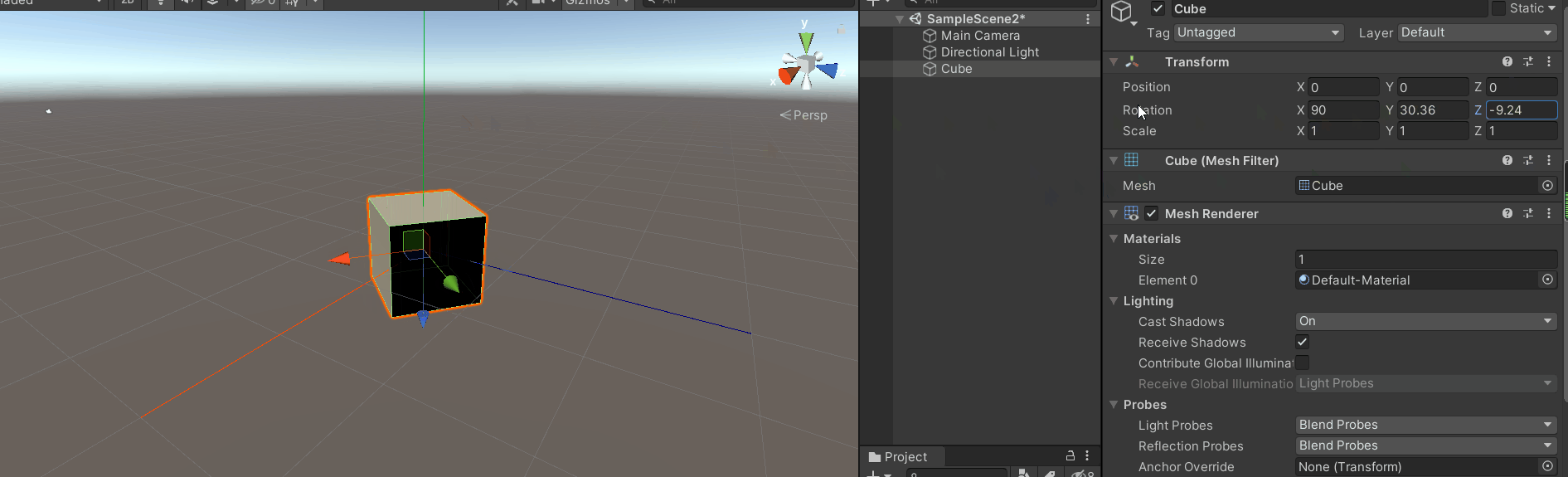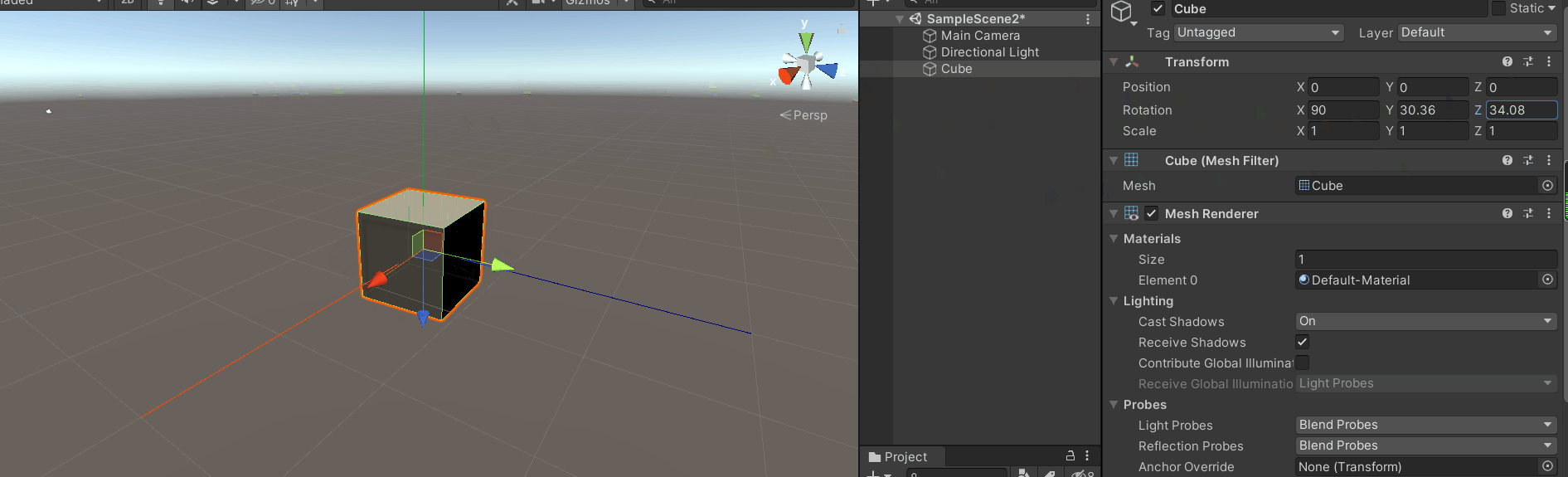
这就是万向锁
你会发现z轴旋转和y轴旋转效果是一样的,同时你会发现z轴(模型坐标系)和y轴坐标(惯性坐标系)平行。
此时y轴(惯性坐标系)旋转面和z轴(模型坐标系)旋转面共面,
从上图很容易看出旋转y轴(惯性坐标系)和旋转z轴(模型坐标系)是一样的效果,只不过方向相反或相同。
总结:
万向锁产生时两个旋转轴平行(旋转面共面)使模型的旋转失去一个方向的旋转。
为什么Unity3d旋转默认采用了有万向节死锁的欧拉角,而不用四元数?
Unity的底层是通过四元数记录物体旋转的,并通过矩阵和四元数实现物体的旋转及插值。
但在上层Unity提供了,向欧拉角进行转换输出,并能够通过欧拉角进设置物体旋转的功能。
一些本通过四元数进行旋转/插值计算的方法,在上层也是通过欧拉角输入对应旋转值。
这是由于相较矩阵和四元数,欧拉角是最接近人类直观思维的一种3D旋转表达模式,应该没有人想通过输入矩阵或者四元数来旋转物体吧...
在底层通过矩阵/四元数,记录完成旋转,避免万向锁,但在上层提供欧拉角的转换输出和旋转设定,这应该说是当下大多数3D引擎架构都普遍采用的一种模式。
此外还要提两点的:
一是,限制欧拉角;
由于存在 四元数--->欧拉角 这样的底层到上层的转换输出,因而就需要引入限制欧拉角规则。
这是由于三角函数是一个周期函数,因而我们进行反三角函数运算的时候,要将输出值限制在一定的范围内,否则会有无穷多解。
其实这也是由于欧拉角的一大缺点之一,因为±360度角度值相同,导致对于同一3D方位/角位移会有无数种表示。
Unity中的欧拉角采用 Y(Heading)-->X(Pitch)-->Z(Bank) 的轴顺序,对应的限制规则,是将Y和Z轴的旋转数值限制在[-180,180],中间X轴旋转数值限制在[-90,90]。
总之就是内外转轴360度全域,中间转轴只有180度半域。
这里给出指定欧拉角的旋转矩阵:

通过m32 = -sinP;
那么Pitch X轴的转值 P = asin(- m32)
之后对于Heading Y轴的转值H

从而![]()
同理,对于Bank Z轴的转值B

从而![]()
注意以上的计算的前提是在Pitch 转值不等于 ±90度,内外转轴不重合时能够成立,否则,我们解 Heading 和 Bank旋转所用到的 m12 m22 m31 m33 将全部为0,无法正常求解。
限制欧拉角规则就已经包含在了转换方法中,因为asin的值域是[-pi/2,pi/2],而atan2的值域是[-pi,pi]。
所以通过transfrom.eulerAngle获取到的欧拉角值就是经过限制后的值。
transfrom.eulerAngle.y/z 直接输出值是在 [0,360]。
transfrom.eulerAngle.x 输出值是 [0,90]U[270,360]。
如果你进行±360度,映射回[-180,180],Y和Z轴转值正好填满[-180,180]而,X轴就变为了[-90,90]。
总归是YZ 360度全域,X只有180度半域。
这种限制欧拉角就导致了一些情况下,transfrom.eulerAngle获取到的旋转角,尤其是针对X轴和预期的有些出入。
并且特别提醒,transfrom.eulerAngle获取到的值,和你在Inspector窗口的Transfrom组件中看到的旋转数值又是不一样的,Unity编辑器又经过了额外的封装。
没错,transfrom.eulerAngle和这里是不一样的,这里是Unity编辑器又经过一次封装产生的效果,允许超限角度的显示输出和设定。

二是,Unity对万向锁的两个处理;
虽然底层通过四元数记录完成旋转,但由于提供了transfrom.eulerAngle属性,因而需要对通过该属性设置旋转角,可能遇到的万向锁时的情况进行相应的处理。
首先是阻止通过transfrom.eulerAngle角度设定插值,使物体转过万向锁的位置(像是有一道锁阻止了物体旋转)。
这是因为Unity中已经通过四元数进行了旋转的记录和完成,因而不提供欧拉角的旋转插值过渡的计算方法。
比如这段代码通过欧拉角来使物体发生绕X轴的旋转:
using UnityEngine;public class Rotate : MonoBehaviour
{// Start is called before the first frame updatevoid Start(){}// Update is called once per framevoid Update(){gameObject.transform.eulerAngles = gameObject.transform.eulerAngles + new Vector3(30 * Time.deltaTime, 0, 0);}
}
其次是,当Pitch正好为±90度时,cosP = 0, sinP = ±1,带入上述矩阵可得:

此时若想解出 Heading Y轴 和 Bank Z轴的旋转量
根据上述推导出的
H = atan2(m31 m33)
B = atan2(m12 m22)
在这种情况下是解不出来的,因为 m31 m33 m12 m22 都变成0了
而矩阵中另外四个分量中,要么只有 H-B 项,要么只有 H+B项,sin和cos的值是相互关联的。
等式/方程就一个,要解的未知数却有两个,就会有无穷多个解,
我们不得不设 Heading 或 Bank 的其中一个为0,才能解出另外一个。
在这种情况下,又出现了欧拉角不唯一的问题,不所以得不令其中一个为0,将旋转完全用另一方表示。
Unity中,是将Z轴(Bank)旋转归0,从而推导出Y轴(Heading)的旋转值。
此时如果我们通过欧拉角旋转Z轴,就会产生类似旋转实际被应用到Y轴上的效果。
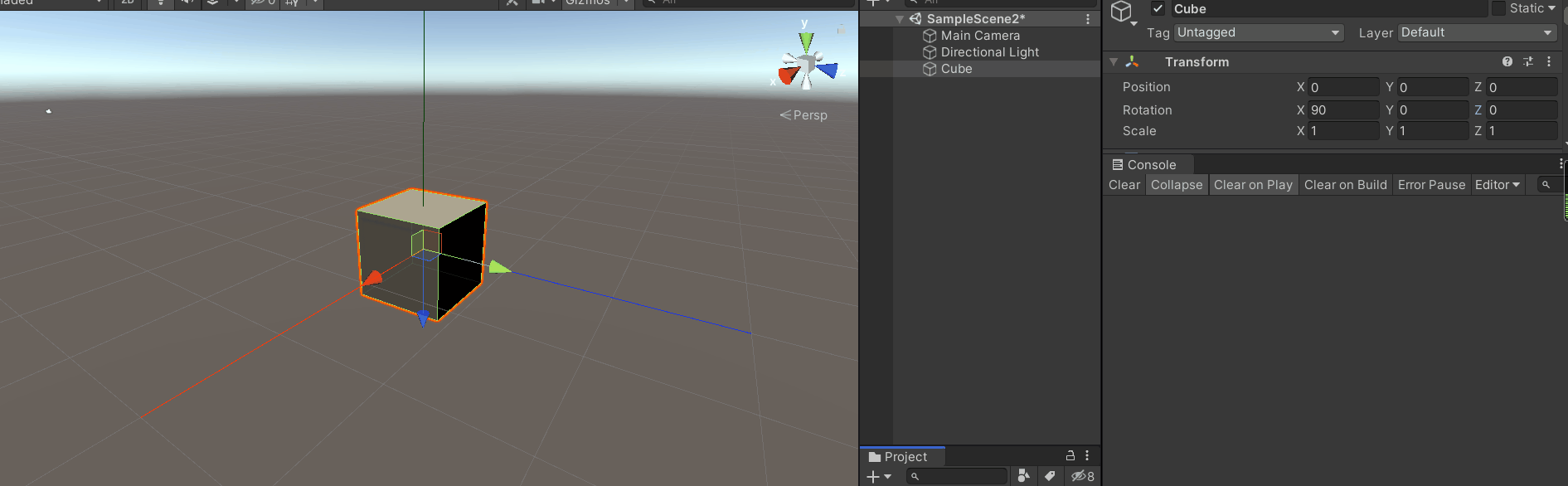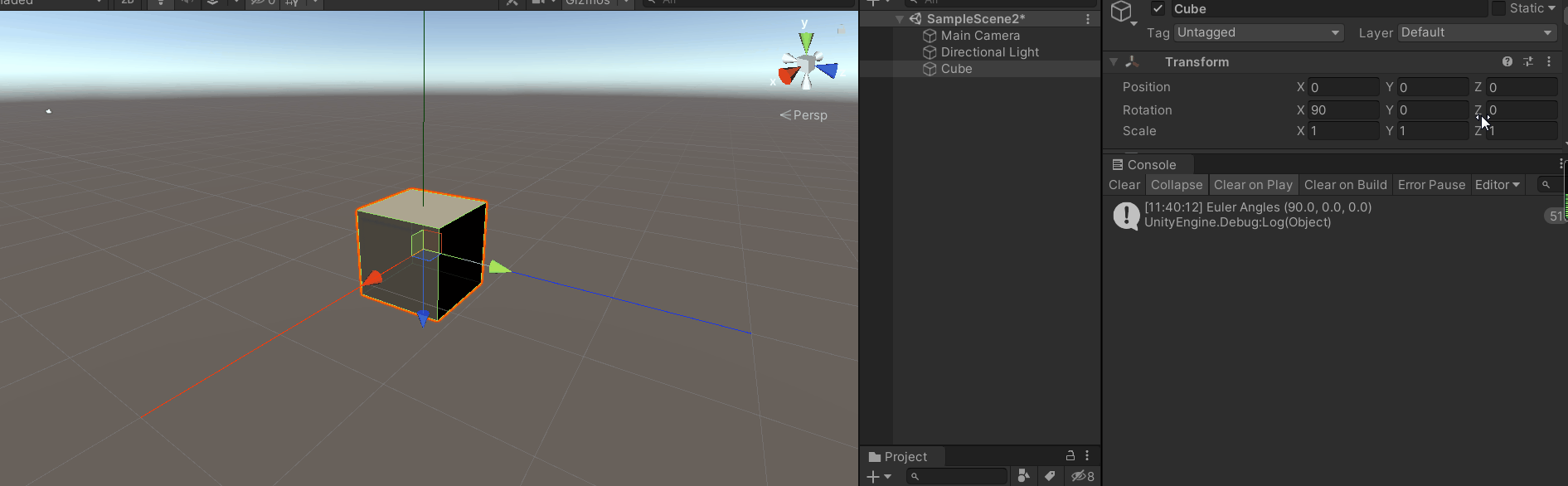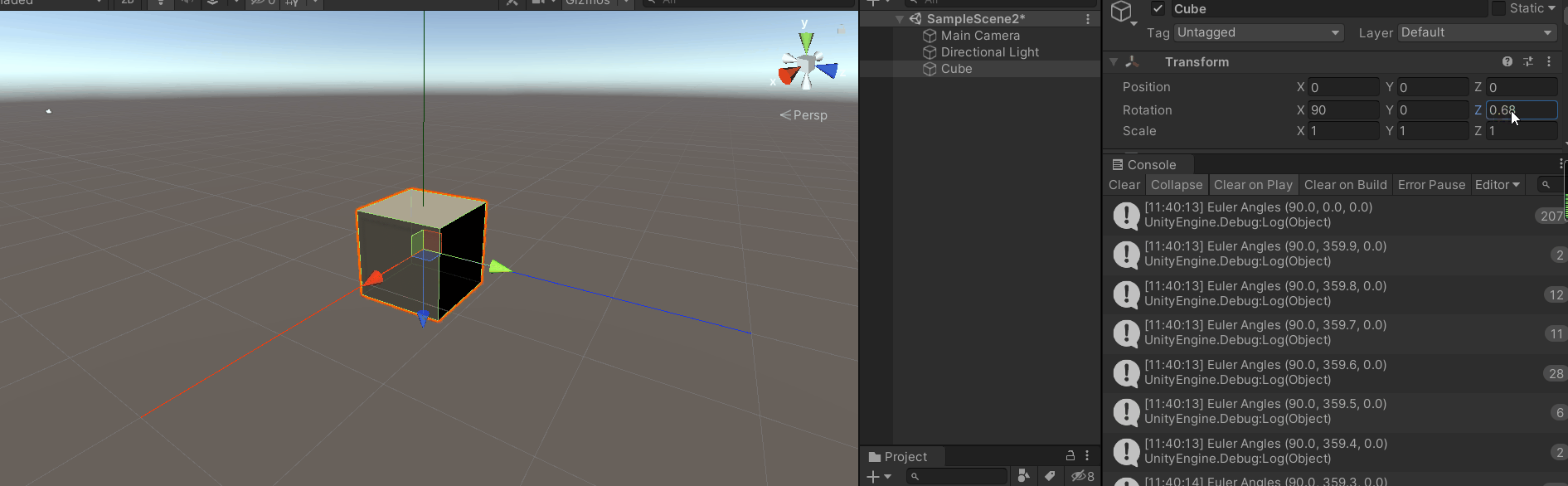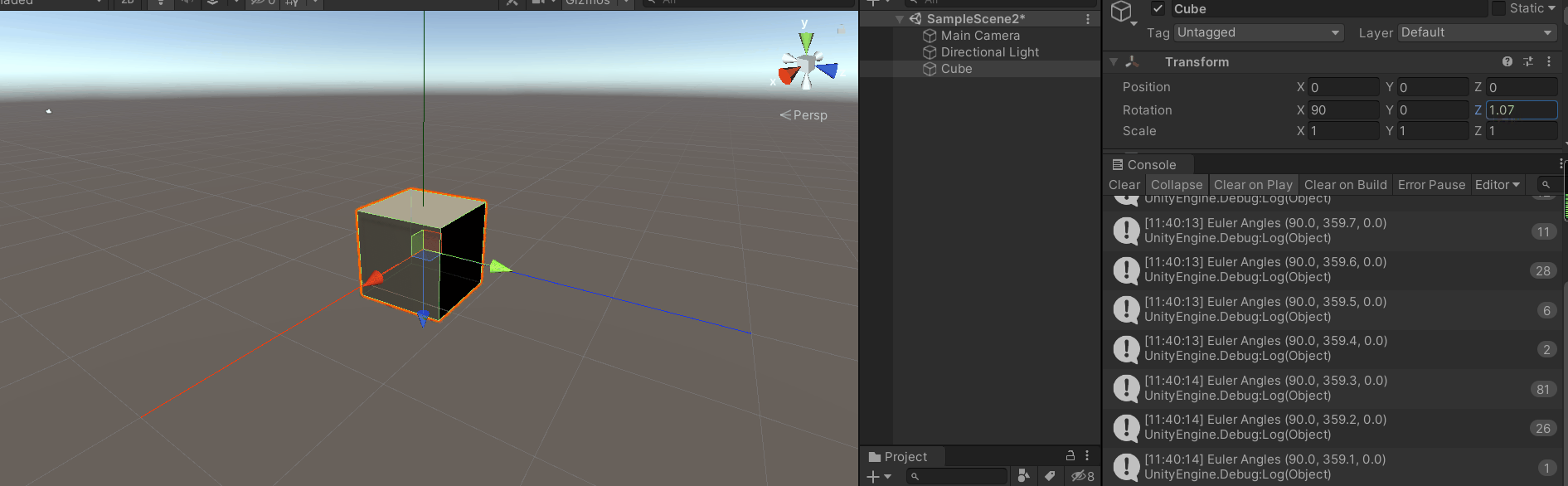
编辑器直接设置X轴旋转值为90度,来到发生万向锁位置,Z轴转置归0,输出Y轴旋转数据。此时我们通过编辑器进行Z轴旋转,可以看到transfrom.eulerAngle.z始终为0,而Y轴旋转数值发生变化,旋转可以看作被应用到了Y轴上。
如何应对万向锁
通过矩阵与四元数实现旋转
一个方法就是不要使用欧拉角来记录旋转,完成旋转的动画差值,而是在底层通过四元数/矩阵来记录/完成旋转
注意!!!这需要我们完全按照矩阵变换/四元数变换,来考虑旋转和旋转的差值,一旦我们尝试将一个欧拉角的旋转,转换到矩阵/四元数,或是尝试从矩阵/四元数反解对应的欧拉角,就一定会出现正旋反解问题。
建议使用四元数,因为四元数有 sphereLerp 方法,对旋转能够实现无任何限制的最短球面差值。
记得在上层的API,我们仍需要给出,对欧拉角进行转换输出/设置的方法。
一些旋转方法的上层调用,也应是通过欧拉角,或者轴-角式,来设置旋转量。
因为相比于矩阵/四元数,欧拉角是最接近人类直观思维的一种旋转表达模式。
可以参考一下Unity,底层通过四元数记录实现旋转,但上层却通过欧拉角的形式表现。
使用特定的轴嵌套顺序
我们可以用特定的欧拉角轴嵌套顺序,将发生万向锁的位置放到不常用的位置上,只要中间的转轴旋转值不接近±90度,欧拉角在记录表现动画差值时就是正常的。
Unity中所偏好的,左手系,Heading Y轴 --> Pitch X轴 --> Bank Z轴,就是给摄像机设计的轴嵌套方案。
它的万向锁位置被放在了摄像机冲向正上方和正下方,对于摄像机而言,很少会有对这两个角度拍摄的情况。
另一种左手系下,给飞行器设计的轴嵌套方案是 Pitch X轴 ---> Yaw Y轴 ---> roll Z轴。
它的万向锁位置是被放在了飞行器冲向正左和正右的时候。
相比于摄像机,飞行器经常需要进行X轴的旋转,起飞时的拉起就是转X轴,甚至需要殷麦曼翻转这样的机动动作。
而冲向正左正右的情况,实际并不会发生,因为目前人类的飞行器还无法做到直角转弯,在转弯时必然留有一定的转弯半径进行盘旋。