Exclusive or

article/2025/9/20 19:34:10

题目连接

题意：
每次给一个n，求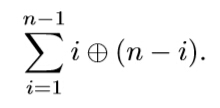
(2≤n<10⁵⁰⁰)
分析：
先说一下自己的想法，如果将n换成二进制数，也就一两千位左右，那么一位一位处理是可以接受的。将0-n写成二进制形式后，显然所有数某一个二进制位是有一个循环节的，那么我们就可以从这里入手直接求解

import java.io.*;
import java.math.*;
import java.util.*;public class Main {public static BigInteger zero = BigInteger.ZERO;public static BigInteger one = BigInteger.ONE;public static BigInteger two = BigInteger.valueOf(2);public static BigInteger three = BigInteger.valueOf(3);public static BigInteger four = BigInteger.valueOf(4);public static BigInteger six = BigInteger.valueOf(6);public static BigInteger Down(BigInteger now, BigInteger L) {BigInteger mid = now.divide(L).multiply(L).add(L.shiftRight(1));if (now.subtract(mid).signum() < 0)return mid;return mid.add(L.shiftRight(1));}public static BigInteger Up(BigInteger now, BigInteger L) {BigInteger start = now.divide(L).multiply(L);BigInteger mid = start.add(L.shiftRight(1));if (now.subtract(mid).signum() < 0)return start.subtract(one);return mid.subtract(one);}public static int getValue(BigInteger now, BigInteger L) {BigInteger mid = now.divide(L).multiply(L).add(L.shiftRight(1));if (now.subtract(mid).signum() < 0)return 0;return 1;}public static BigInteger solve(BigInteger nl, BigInteger nr, BigInteger gl, BigInteger L) {BigInteger ret = zero, step = Down(nl, L).subtract(nl), t = nr.subtract(Up(nr, L));if (step.subtract(t).signum() > 0)step = t;while (nl.add(step).subtract(gl).signum() <= 0) {if ((getValue(nl, L) ^ getValue(nr, L)) == 1)ret = ret.add(step);nl = nl.add(step); nr = nr.subtract(step);step = Down(nl, L).subtract(nl); t = nr.subtract(Up(nr, L));if (step.subtract(t).signum() > 0)step = t;}if (gl.subtract(nl).add(one).signum() >= 0 && (getValue(nl, L) ^ getValue(nr, L)) == 1)ret = ret.add(gl.subtract(nl).add(one));return ret;}public static void main(String[] args) {BigInteger n, L, tans, nl, ans;Scanner cin = new Scanner(System.in);while (cin.hasNext()) {n = cin.nextBigInteger();L = two;ans = zero;while (L.subtract(n.shiftLeft(1)).signum() <= 0)//(L <= n * 2){tans = zero;if (n.divide(L).shiftRight(1).signum() > 0) {tans = solve(zero, n, L.subtract(one), L);}nl = n.divide(L).shiftRight(1).multiply(L);tans = n.divide(L).shiftRight(1).multiply(tans).add(solve(nl, n.subtract(nl), n.subtract(one).shiftRight(1), L));ans = ans.add(tans.multiply(L));L = L.shiftLeft(1);}System.out.println(ans.subtract(n.shiftLeft(1)));}}   
}

学习一下题解的方法，关键在于：(2 * k) ^ x = (2 * k + 1) ^ x
之后就学习一下题解的公式化简方法了

import java.util.*;
import java.math.*;public class Main {static BigInteger n, ret;static BigInteger one = BigInteger.valueOf(1);static BigInteger two = BigInteger.valueOf(2);static BigInteger four = BigInteger.valueOf(4);static BigInteger six = BigInteger.valueOf(6);static HashMap<BigInteger, BigInteger> mp = new HashMap<BigInteger, BigInteger>();public static BigInteger fun(BigInteger n) {if (n.equals(BigInteger.ZERO) || n.equals(BigInteger.ONE)) return BigInteger.ZERO;if (mp.containsKey(n))return mp.get(n);BigInteger k = n.shiftRight(1);if (n.testBit(0)) {ret = four.multiply(fun(k)).add(six.multiply(k));mp.put(n, ret);return ret;}else {ret = (fun(k).add(fun(k.subtract(one))).add(k.shiftLeft(1)).subtract(two)).shiftLeft(1);mp.put(n, ret);return ret;}}public static void main(String[] args) {Scanner cin = new Scanner(System.in);while (cin.hasNext()) {n = cin.nextBigInteger();mp.clear();System.out.println(fun(n));}}
}