1. Python中的turtle模块制图

前面已经讲了递归的原理，这里用递归作图来直观的理解递归。
首先了解以下Python中用于作图的内置海龟作图系统turtle module。
Python内置，随时可用，以LOGO语言的创意为基础。
其意象为模拟海龟在沙滩上爬行而留下的足迹。

爬行：forward(n); backward(n)
转向：left(a); right(a)
抬笔放笔：penup(); pendown()
笔属性：pensize(s); pencolor( c )

1.1 画一条带方向的直线

import turtlet = turtle.Turtle()  # 开始作图
t.forward(100)  # 指挥海龟作图
turtle.done()  # 结束作图

1.2 画一个正方形

import turtlet = turtle.Turtle()for i in range(4):t.forward(100)  # 往前走100的距离t.right(90)  # 向右旋转90度turtle.done()

1.3 画一个星星

import turtlet = turtle.Turtle()
t.pencolor('red')  # 设置线条的颜色
t.pensize(5)  # 设置线条的粗细
for i in range(5):t.forward(100)t.right(144)
t.hideturtle()  # 将箭头隐藏
turtle.done()

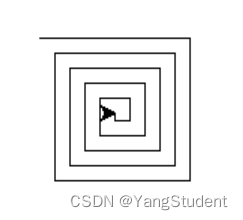
1.4 画一个螺旋的图，用递归的方法

import turtlet = turtle.Turtle()def draw_spiral(line_len):  # line_len是最开始的线的长度if line_len > 0:  # 最小规模，当线的长度小于0时，结束。t.forward(line_len)t.right(90)draw_spiral(line_len - 5)  # 调用自身，每次线的长度减小，向最小规模演进。draw_spiral(100)turtle.done()

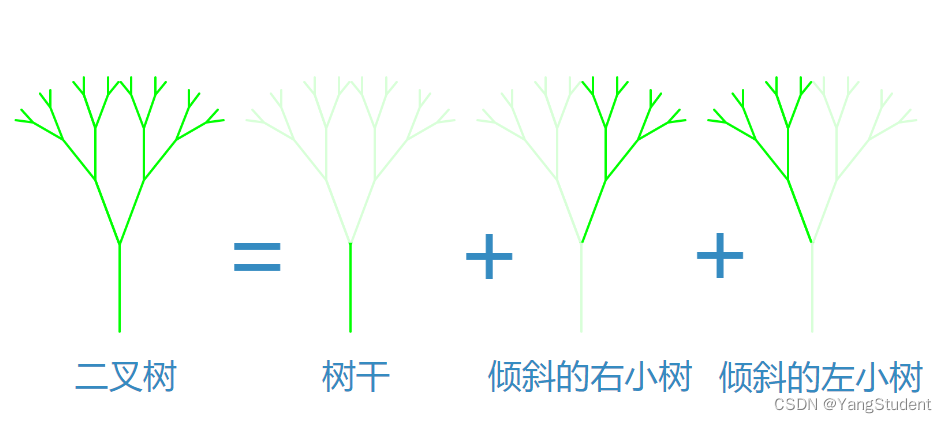
2. 用turtle画一个分形树

分形树就是每棵树都是由树干+左小树+右小树组成的，如图所示。最小的左（右）小树只有三根线。

import turtlet = turtle.Turtle()
t.left(90)
t.penup()  # 提笔，意思是，轨迹正常走，但是不画出来，可以避免画出不必要的路径
t.backward(100)  # 向箭头的反向走100
t.pendown()
t.pencolor('green')  # 树的颜色设置为绿色
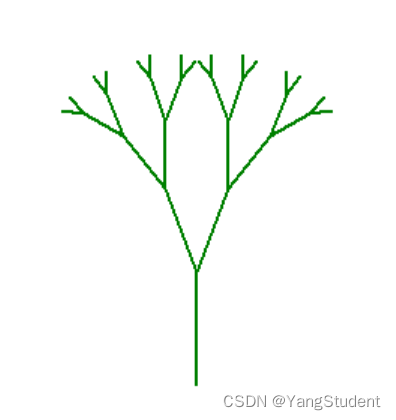
t.pensize(2)  # 线的宽度def tree(branch_len):if branch_len > 5:  # 树干太短时，不画，递归结束t.forward(branch_len)  # 画树干t.right(20)  # 向右画长为20的右边（右子树的一部分）tree(branch_len - 15)  # 递归调用，画右子树t.left(40)  # 向左倾斜40°，即画向左的20°的左子树tree(branch_len - 15)  # 递归调用，画右子树t.right(20)  # 向右回正t.backward(branch_len)  # 海龟回到原来的位置tree(75)  # 画树干为75的分形树
t.hideturtle()
turtle.done()

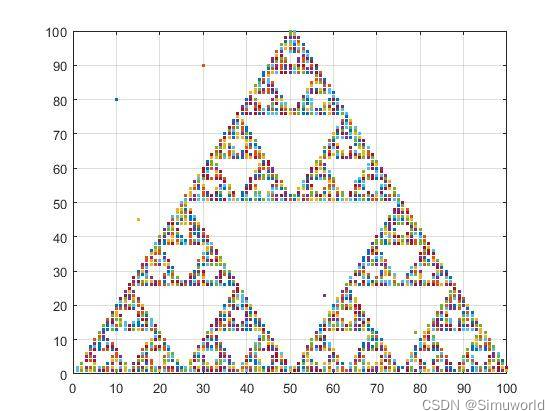
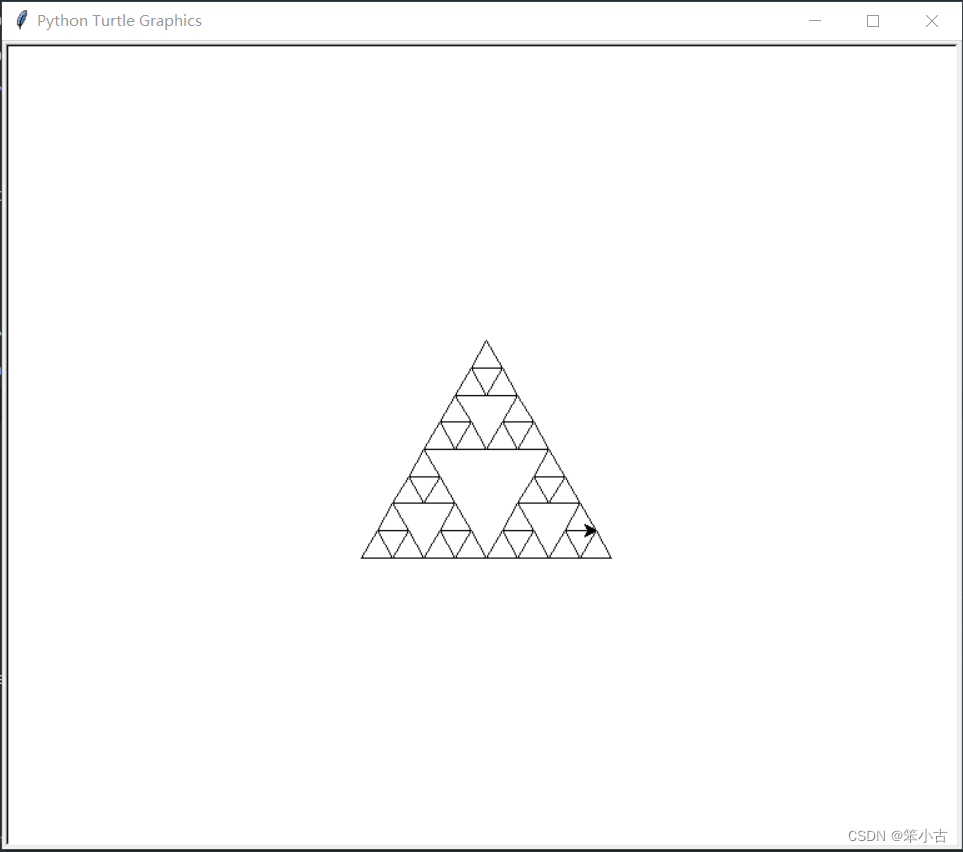
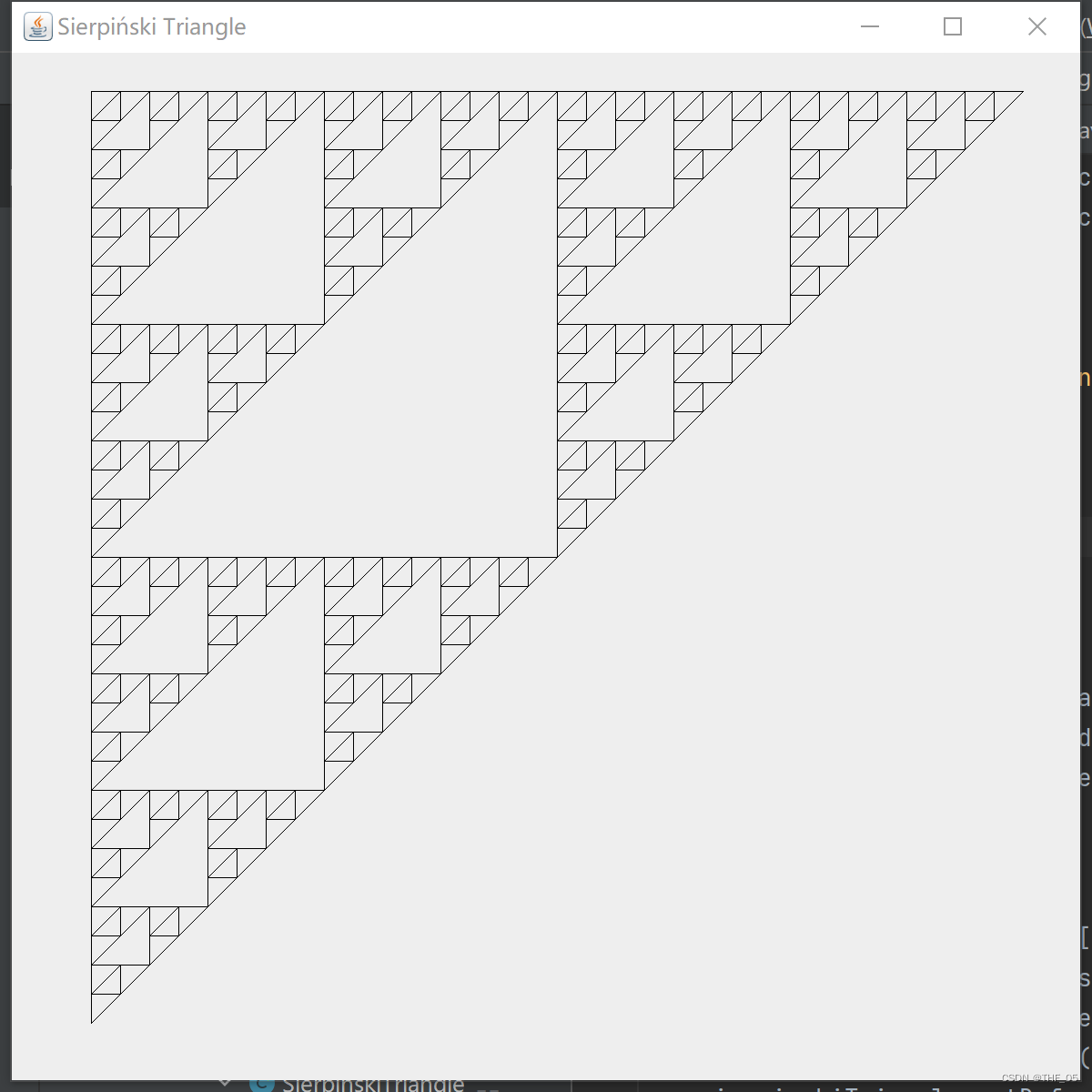
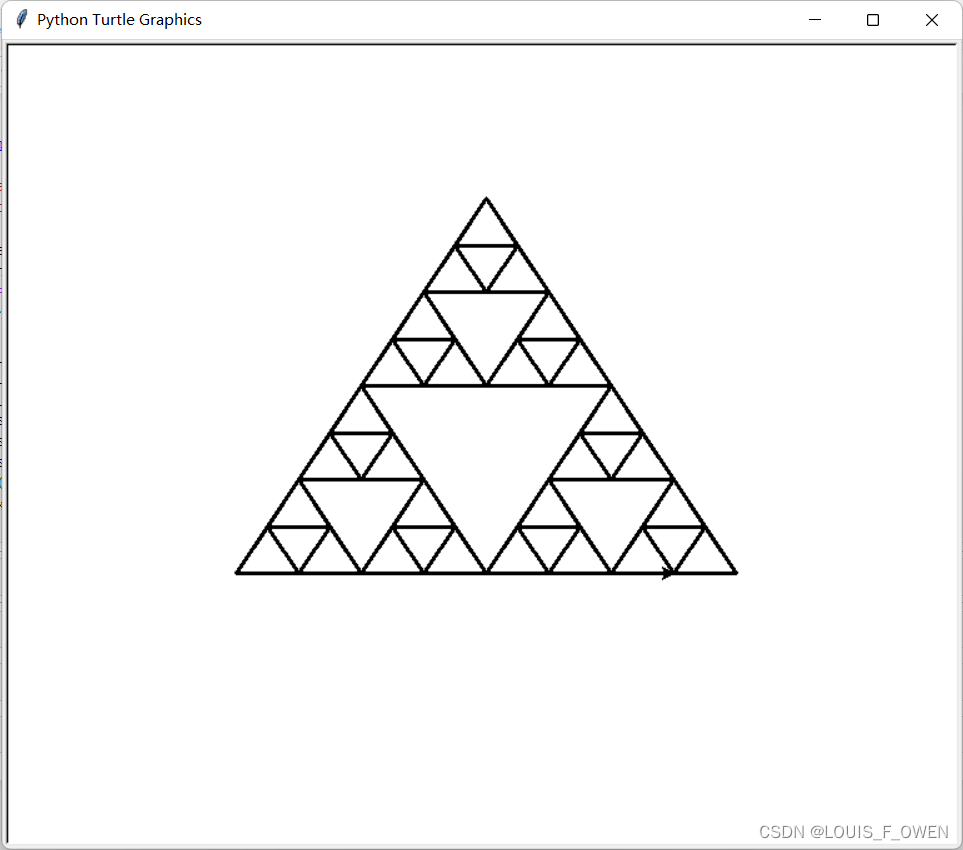
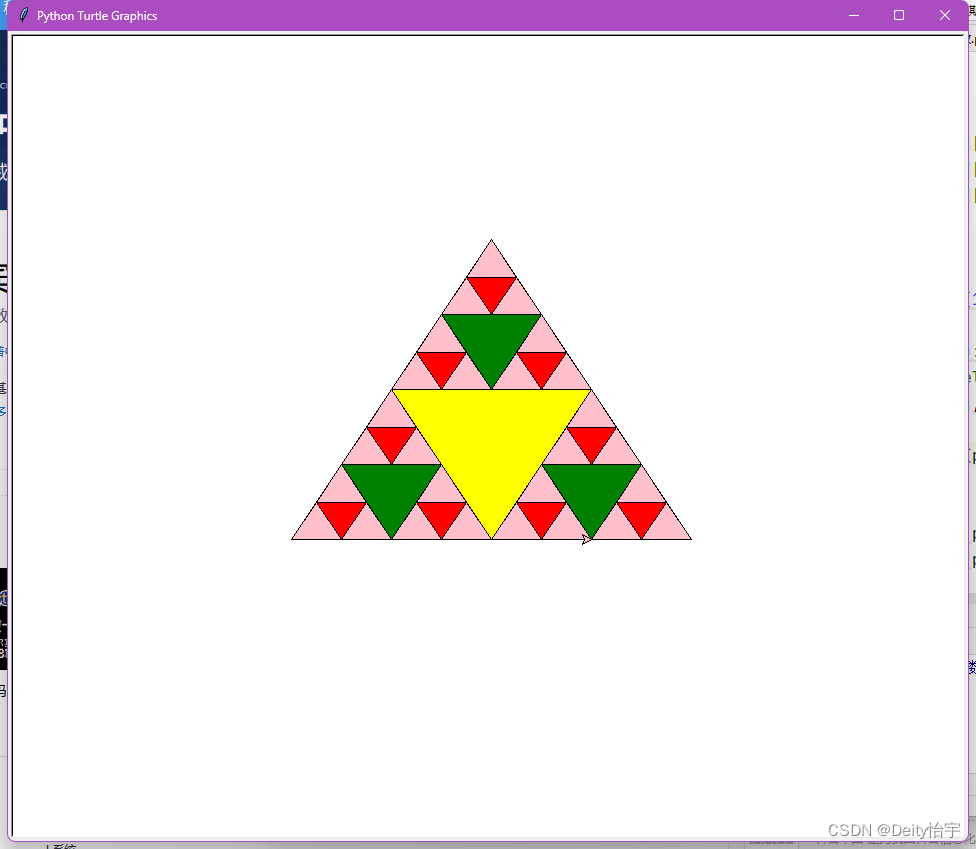
3. 谢尔宾斯基三角形

谢尔宾斯基三角形，也具有与分形树类似的自相似性（就是每一个小部分和大部分的结构是相似的）。
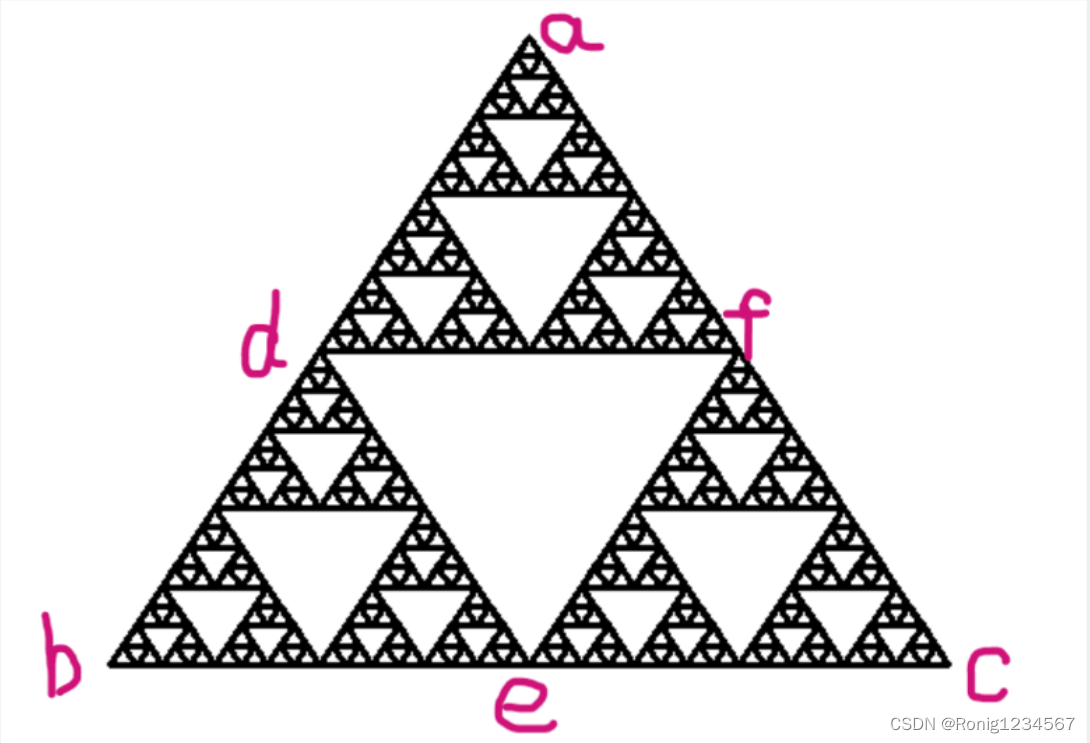
谢尔宾斯基三角形是由3个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成。
真正的谢尔宾斯基三角形是无限个小三角组成的，因此我们只能做有限个谢尔宾斯基三角形。

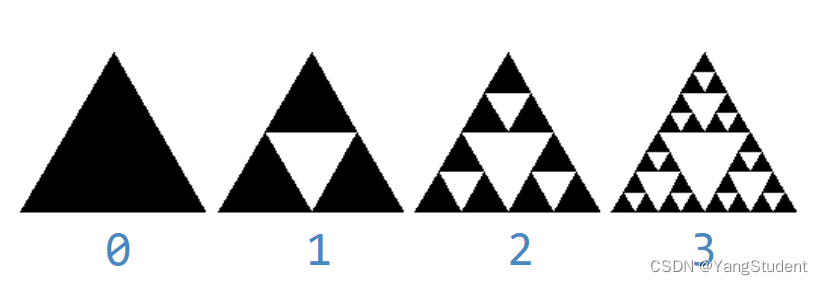
引入一个degree的概念。
当只有一个三角形时，degree是0，这也是递归的结束条件。
当degree是1时，degree=1的三角形，由三个degree=0的三角形组成。
当degree是2时，degree=2的三角形，由三个degree=1的三角形组成。
…
…
以此类推。
在degree有限的情况下，degree=n的三角形，是由3个degree=n-1的三角形按照品字形拼叠而成。

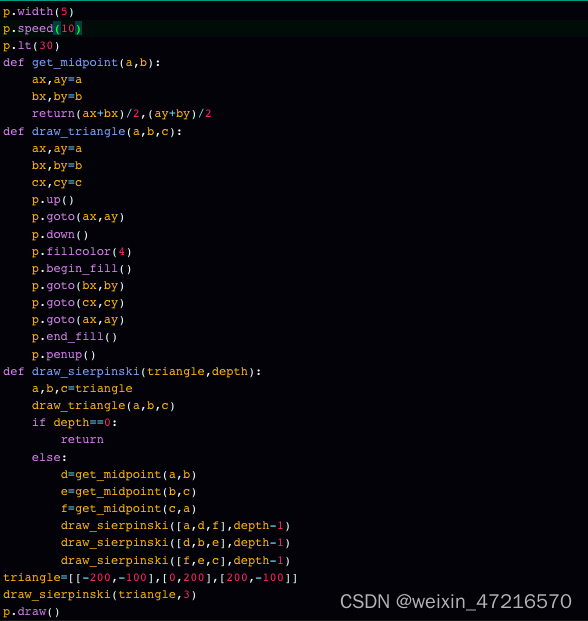
代码：画一个degree = 5的谢尔宾斯基三角形

import turtlet = turtle.Turtle()def draw_triangle(points, color):  # 这个函数，用来画三角形。color参数，是自己设置的，填充三角形的颜色。t.fillcolor(color)  # 设置填充颜色t.penup()  # 抬笔t.goto(points['top'])  # 让小海龟朝着这个方向移动t.pendown()  # 落笔t.begin_fill()  # 开始填充颜色t.goto(points['left'])t.goto(points['right'])t.goto(points['top'])t.end_fill()  # 停止填充颜色def get_mid(p1, p2):  # 找两个点间的中点return (p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2def sierpinski(degree, points):colormap = ['blue', 'red', 'green', 'white', 'yellow', 'orange']draw_triangle(points, colormap[degree])  # 画等边三角形，不同度数的三角形颜色不同if degree > 0:  # 递归结束条件sierpinski(degree - 1,  # 朝递归结束条件演进{'left': points['left'],'top': get_mid(points['left'], points['top']),  # 减小规模，边长减半'right': get_mid(points['left'], points['right'])})sierpinski(degree - 1,{'left': get_mid(points['left'], points['top']),'top': points['top'],'right': get_mid(points['top'], points['right'])})sierpinski(degree - 1,{'left': get_mid(points['left'], points['right']),'top': get_mid(points['top'], points['right']),'right': points['right']})points = {'left': (-200, -100), 'top': (0, 200), 'right': (200, -100)}  # 三角形外轮廓的三个点
sierpinski(5, points)
turtle.done()