1、浮点数理解
在平常的代码编写中大家经常用到float 32、double 64等,但是否有深入的去了解一下这类数据是怎么表示的呢?今天我们就去学习浮点数的表示方法,以及其优缺点。
首先浮点数为什么叫浮点数呢?因为浮点数的小数点的位置不是固定不变的,是浮动的,所以就称之为浮点数;与之相对,那定点数就是小数点位置固定不变的数了。
浮点数一般由三部分组成,其分别为【符号位S】、【阶码E】、【尾数M】,此外还有一个重要的组成部分为【基数R】,不过一般基数固定为2,因此我们不做过多讨论。
当前的浮点数使用IEEE754标准,以float 32为例,其在计算机中的存储格式如下:
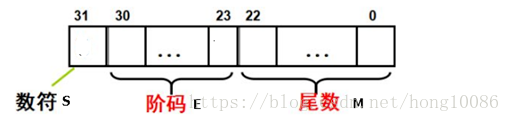
其中符号位占1位、阶码位占8位、尾数位占23位
【符号位S】、【阶码E】、【尾数M】与该数所表示数值的关系见以下公式:
![]()
其中1.M涉及一个知识点----“存储数据规格化”,即要求【尾数M】的绝对值需要大于基数的倒数,公式表达如下: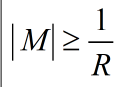 ,当R为2时,
,当R为2时,![]() 。因此就规定,尾数的第一位为1;因为都为1,所以在存储时该位会被省略,但在计算时我们需要将它加上。
。因此就规定,尾数的第一位为1;因为都为1,所以在存储时该位会被省略,但在计算时我们需要将它加上。
eg1:使用32位浮点数表示小数-3.75

所以:【符号位S = 1】、【阶码E = 1000 0000】、【尾数M = 1110 0000 0000 0000 0000 0000】
2、定点数理解
定点数即为小数点固定的数,以常见的int型数据,即为小数点位于末尾的定定点数。与浮点数相比,定点数最大的特点是“乘以基数可以通过对数据的移位进行操作(像int数乘2可以左移1位实现)”,但由于浮点数不同位有不同的含义,无法通过移位进行操作。
eg2:使用8位定点数表示小数-0.75(规定8位定点数由1个符号位,0个整数位,7个小数位组成)
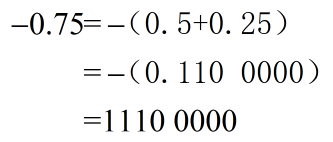
表示的最大正数:0111 1111 即为:0.5+0.25+0.125+0.0625+0.03125+0.015625+0.0078125 = 0.9921875
表示的最大负数:1111 1111 即为:-(0.5+0.25+0.125+0.0625+0.03125+0.015625+0.0078125)= - 0.9921875
表示的最小正数:0000 0001 即为:0.0078125
表示的最小负数:1000 0001 即为:- 0.0078125
表示精度为:![]()
定点数缺点:定点数表示法简单直观,但是数值表示的范围太小,运算时容易产生 溢出。因此在计算时采用表示范围较大的数存储中间变量。
3、浮点数与定点数相互转换
假定8位定点数由1个符号位,4个整数位,3个小数位组成(即Q定标3)
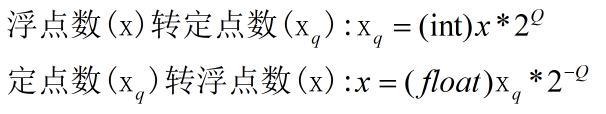
eg3:使用定标为Q3的8位定点数表示浮点数x=0.6
![]()
用二进制表示4为:0 0000 100
eg4:将Q3表示的8位定点数0 0000 100转换为浮点数
![]()
从以上的eg3与eg4可以看出,浮点数在转换为定点数的过程中,产生了误差(0.6变为了0.5)。
为了最大限度的保持数的精度,在将浮点数转化为定点数前,可以采用四舍五入的方法,即在进行向下取整运算前,先加上0.5,即
![]()
重复计算eg3与eg4,![]() ,
,![]() ;可以明显看出,数据的表示误差减小了。(0.6变为了0.625)
;可以明显看出,数据的表示误差减小了。(0.6变为了0.625)
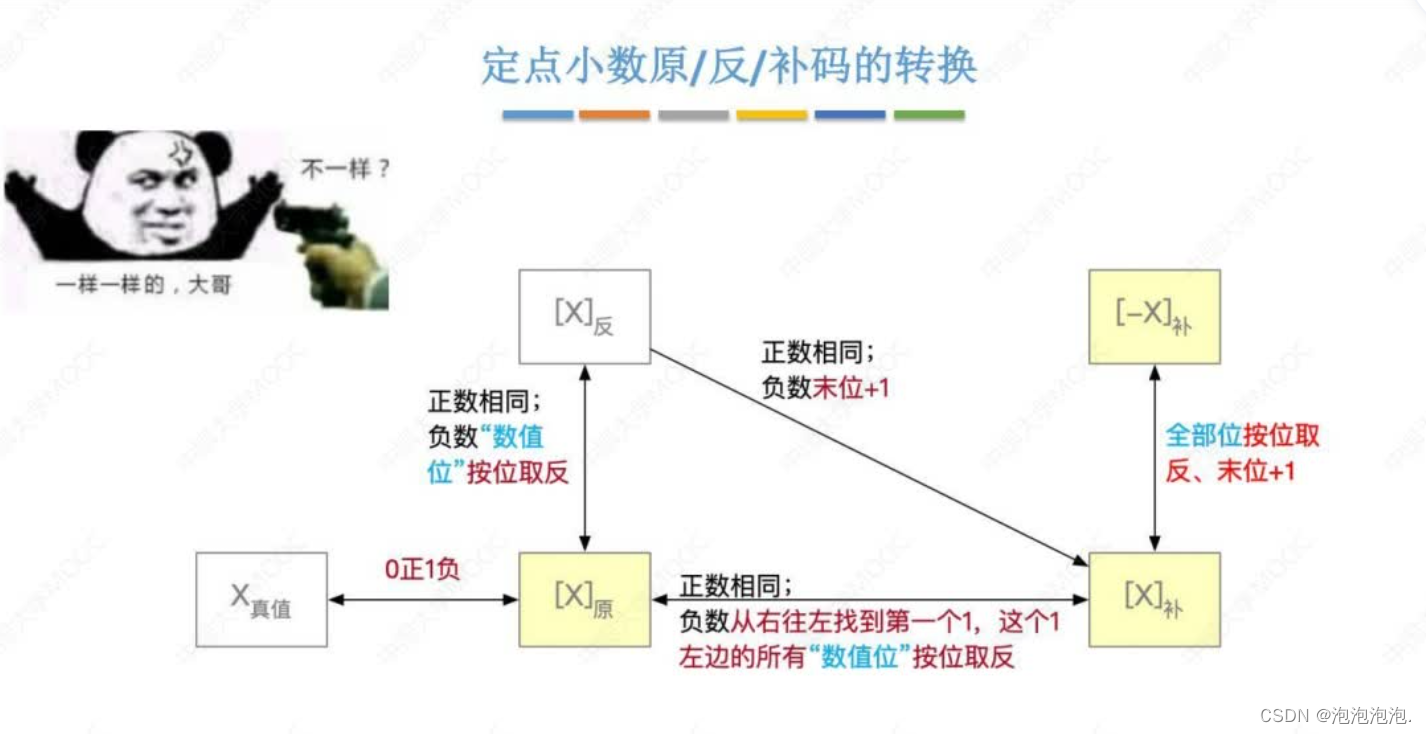
注:①本文受限于笔者基础知识水平,在以上分析时,未考虑反码与补码的问题;
②“存储数据规格化”相关知识理解较浅
若读者发现以上文章有错误,麻烦在评论区指出,我会积极更正。
如果认为该文章有帮助,请点个赞,您的点赞是对我最大的鼓励。
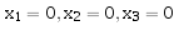

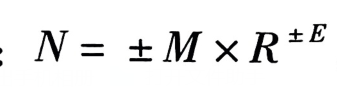





![[计算机组成原理]2-4、定点数详解](https://img-blog.csdnimg.cn/f89911ec3b3f439dae8c7ec9d27c5c95.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80ODMxMjQ4NA==,size_16,color_FFFFFF,t_70#pic_center)