tip:表示方法，可见定点数(fixed-point number)的表示方法
参考文档：定点数与浮点数：https://www.cnblogs.com/kevinq/p/4480563.html
FPGA的算法解析3 定点数与浮点数：https://zhuanlan.zhihu.com/p/472748886
定点数运算：https://blog.csdn.net/limanjihe/article/details/52440544
定点运算——乘法：https://blog.csdn.net/Blackoutdragon/article/details/104863319
计算机组成原理 定点运算-移位、加、减、乘、除（详细解析-看完就会）：https://zhuanlan.zhihu.com/p/150650554

1. 定点数

定点数中小数点的位置由两个参数确定，一个是定点数的位宽 w，小数位的位宽 wf 。



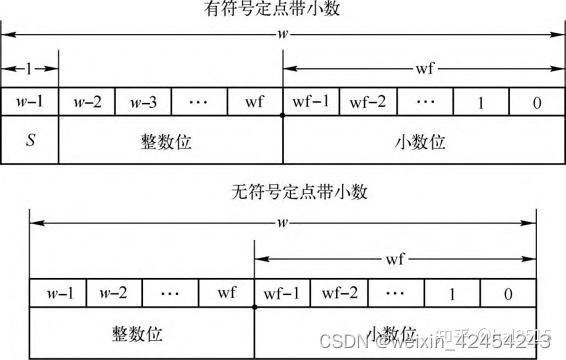
下面给出一个例子，2Q6（Fix9_6）

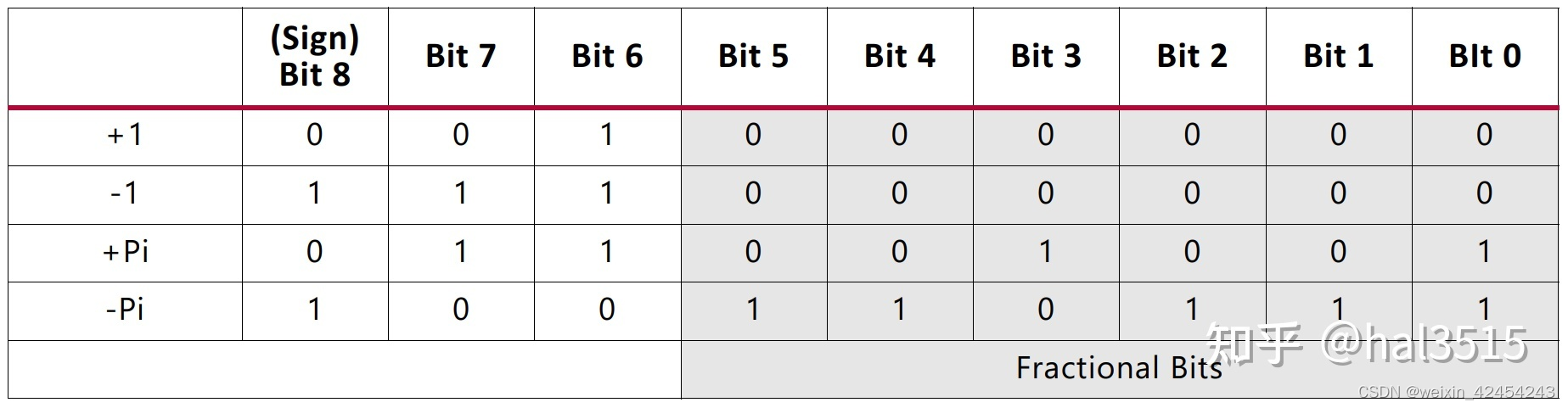
2Q6 包含一个 1 个符号位，2 个整数位，6 个小数位。

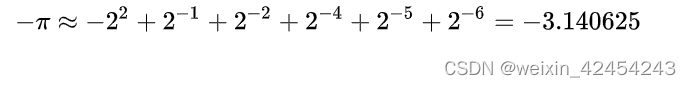
2. 定点数加减运算

不论操作数是正还是负，在做补码加减法时，只需将符号位和数值部分一起参与运算，并且将符号位产生的进位丢掉即可。如：

short A=-9, B=-5;
cout<<A+B<<endl;  //-14

推导过程如下（A与B都是定点数表示的纯整数）：
A的原码为：1000 0000 0000 1001，因此补码为：1111 1111 1111 0111
B的原码为：1000 0000 0000 0101，因此补码位：1111 1111 1111 1011
A+B的补码为：1 1111 1111 1111 0010，将符号位产生的进位丢掉，因此最终结果为：
1111 1111 1111 0010，结果的原码为：1000 0000 0000 1110，即-14。

注：书写约定整数的符号位与数值位之间用逗号隔开，小数的符号位与数值位之间用小数点隔开。

定点数计算

• 定点数相加时，将两数二进制的小数点对齐，直接相加；
• 定点数相减时，将减数化为补码后相加。
• 定点数乘法与普通小数乘法一致，但在相加前进行补位，将加数左侧对齐。

3. 定点数加减运算的溢出判断

3.1 用一位符号位判断溢出

对于加法，只有在正数加正数和负数加负数两种情况下才可能出现溢出，符号不同的两个数相加是不会溢出的。
对于减法，只有在正数减负数和负数减正数两种情况下才可能出现溢出，符号相同的两个数相减是不会溢出的。

由于减法运算在机器中是用加法器实现的，因此：不论是作加法还是减法，只要实际操作数（减法时即为被减数和“求补”之后的减数）的补码符号位相同，而结果的符号位又与操作数补码符号位不同，即为溢出。（进一步解释：两个符号位相同的补码相加，如果和的符号位与加数的符号相反，则表明运算结果溢出；两个符号位相反的补码相减，如果差的符号位与被减数的符号位相反，则表明运算结果溢出。）如：

在4位机中，A=5，B=-4，则A-B溢出，推导过程如下：
A的原码为0101，补码为0101；
-B的原码为0100，补码为0100；
A-B的补码为1001，结果的符号位为1，实际操作数的符号位为0，因此溢出。

一位符号位判断溢出方法不仅需要判断加法运算的结果，而且需要保持原操作数。

3.2 用两位符号位判断溢出

此时判断溢出的原则是：当2位符号位不同时，表示溢出；否则无溢出。不论是否发生溢出，高位符号位永远代表真正的符号。

运算结果的符号位为01表明两个正数相加，结果大于机器所能表示的最大正数，称为上溢；运算结果的符号位为10表明两个负数相加，结果小于机器所能表示的最小负数，称为下溢。

也就是说，两个正数相加，数值位不应向符号位同时产生进位，使得结果数的符号位和操作数的一样，为00：

00+00+00（进位）=00   （mod 4）

两个负数相加，数值位应向符号位产生进位，使得两个负数的双符号位的运算为11；

11+11+01（进位）=11   （mod 4）

当运算结果的两个符号位不相同时，表明出现了溢出。判断溢出的逻辑表达式：　　
　　其中Z′为增加的符号位。

　　例：设x=+1100，y=+1000，求6位双符号位补码之和[x+y]补。解：[x]补=001100, [y]补=001000[x+y]补=001100+001000=010100[x+y]补=010100，其中两个符号位出现01，表示已溢出。

　　例：设x=-1100,y=-1000，求6位双符号位补码之和[x+y]补。解：[x]补=110100， [y]补=111000[x+y]补=110100+111000=101100[x+y]补=101100，其中两个符号位出现10，表示已溢出。

　　例：设x=-0.1011，y=-0.0111，则x+y溢出，推导过程如下：解：x的原码为11.1011，补码为11.0101；y的原码为11.0111，补码为11.1001，因此x+y的补码为1 10.1110，将符号位产生的进位丢掉，则结果为10.1110，因此溢出。

　　例：设x=0.1011，y=0.0111，则x+y溢出，推导过程如下：解：x的原码为00.1011，补码为00.0101；y的原码为00.0111，补码为00.1001，因此x+y的补码为01.0000，则结果为01.0000，因此溢出。

采用双符号位补码后，任何小于1的正数，两个符号位都是0；任何大于-1的负数，两个符号位都是1。如果两个数相加后，其结果的符号位出现01或10时，表示发生溢出。因为两个绝对值小于1的数相加，其结果不会大于或等于2，所以最高位总是表示正确的符号。这也可以表示为：当最高数据位有进位而符号位无进位时产生上溢出（01）；当最高数据位无进位而符号位有进位时，表示下溢出（10）。

在双符号位补码中，正常的数据中两个符号位总是相同的，所以在存储数据时不必重复存储，只是在将数据送往运算部件进行运算时才把符号位进行复制形成双符号位补码。

3.3 最高位和次高位判断溢出

利用数据编码的**最高位（符号位）和次高位（数值部分的最高位）**的进位状况来判断运算结果是否发生了溢出。

两个补码数实现加减运算时，若最高数值位向符号位的进位值与符号位产生的进位输出值不相同，则表明加减运算产生了溢出。因为当x和y均为n+1位正整数时，其和有两种情况：当x+y<2n时，不会发生溢出；当x+y≥2n时符号位没有进位，表明发生溢出。当x和y都是n+1位负数时，其和也有两种情况：当x+y≥-2n时，不会发生溢出；当x+y<-2n时，符号位相加后变成0并且有进位，而数值部分的最高位相加时无进位，结果变为正数，表明发生了溢出。减法的情况与此类似，这种判断方法的逻辑表达式如下：

　　例：设x=+1011， y=+1001，求[x+y]补。解：[x]补=01011， [y]补=01001[x+y]补=01011+01001=10100两个正数相加，最高两位的进位为01，表示发生了溢出，其结果为负数，显然是错误的。

　　例：设x=-1101，y=-1011，求[x+y]补。解：[x]补=10011， [y]补=10101[x+y]补=10011+10101=01000两个负数相加，最高两位的进位为10，表示发生了溢出，其结果为正数，显然是错误的。

4. 乘法运算

4.1 分析笔算乘法

设A=0.1101，B=0.1011，求A×B。

1. 对于定点数的乘法，分为两部分

• 将乘数和被乘数的符号位提出，单独进行异或运算
• 将将乘数和被乘数的数值部分取绝对值们，进行移位加法运算

2. 通过下述对笔算的分析，得到对于二进制的乘法数值部分而言，只有两种运算过程

• 乘数对应的位数为0，不加被乘数
• 乘数对应的位数为1，那就进行相应的移位之后，加上对应的被乘数

3. 得到最终对应的结果
   
   所以 A×B=+0.10001111
   　　可见，这里包含着被乘数4的多次左移，以及四个位积的相加运算。
   若计算机完全模仿笔算乘法步骤，将会有两大困难：其一，将四个位积一次相加，机器难以实现；其二，乘积位数增长了一倍，这将造成器材的浪费和运算时间的增加。为此，对笔算乘法做些改进。

4.2 笔算乘法的改进

将A•B= A•0.1011
　　　　 =0.1A+0.001•A+0.0001•A
　　　　 =0.1A+0.00•A+0.001(A+0.1A）
　　　　 =0.1A+0.01[0•A+0.1(A+0.1A)]
　　　　 =0.1{A+0.1[0•A+0.1(A+0.1A)]}
　　　　 =2^-1{A+2^-1 [0•A+2^-1 (A+2^-1A)]}
　　　　 =2^-1{A+2^-1 [0•A+2^-1 (A+2-^-1(A+0))]}

由上式可见，两数相乘的过程，可视作加法和移位(乘2^-1相当于做一位右移)两种运算，这对计算机来说是非常容易实现的。
　　从初始值为0开始，对上式作分步运算，则
　　第一步：被乘数加零　　　　　　A+0=0.1101+0.0000=0.1101
　　第二步：右移一位，得新的部分积　　　2^-1 (A+0)＝0.01101
　　第三步：被乘数加部分积　A+2^-1(A+0)=0.1101+0.01101=1.00111
　　第四步：右移一位，得新的部分积　2^-1 A+2^-1 (A+0)=0.100111
　　第五步：　　　　　　　　0•A +2^-1 [A+2^-1(A+0)] =0.100111
　　第六步：　　　　　　2^-1{0•A+2^-1 [A+2^-1 (A+0)]}=0.0100111
　　第七步：　　　　　　A+2^-1{0•A+2^-1 [A+2^-1 (A+0)]}=1.0001111
　　第八步：　　2^-1 {A+2^-1 [0•A+2^-1 (A+2^-1 (A+0))]}=0.10001111

上述运算过程可归纳为：
　　①乘法运算可用移位和加法来实现，当两个四位数相乘，总共需做四次加法和四次移位。
　　②由乘数的末位值确定被乘数是否与原部分积相加，然后右移一位，形成新的部分积；同时，乘数也右移一位，由次低位作新的末位，空出最高位放部分积的最低位。
　　③每次做加法时，被乘数仅仅与原部分积的高位相加，其低位被移至乘数所空出的高位位置。

计算机很容易实现这种运算规则。用一个寄存器存放被乘数，一个寄存器存放乘积的高位，又用一个寄存器存放乘数及乘积的低位，再配上加法器及其他相应电路，就可组成乘法器。又因加法只在部分积的高位进行，故不但节省了器材，而且还缩短了运算时间。

4.3 图示

原文图示见：https://blog.csdn.net/Blackoutdragon/article/details/104863319

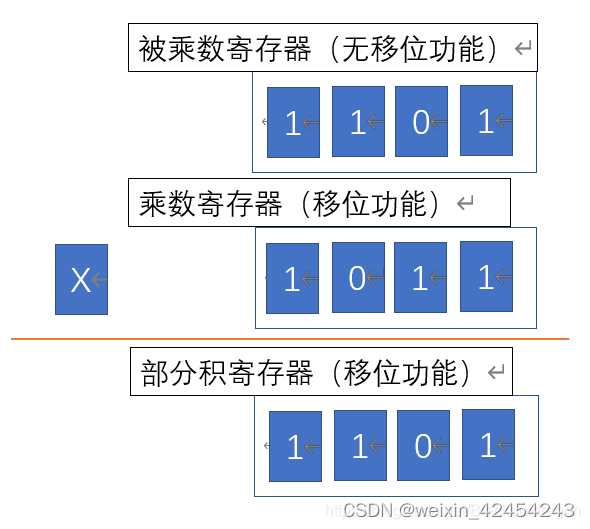
最低位是1，将被乘数加到部分积中。

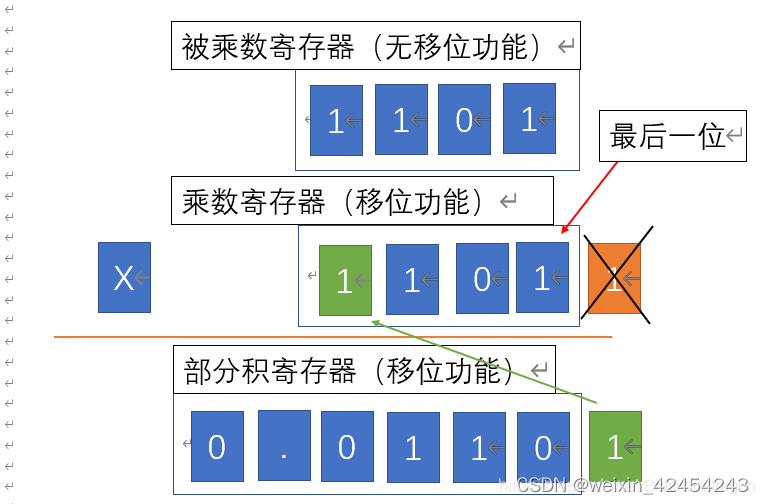
将乘数中已经判定过的1，移除，丢弃已经没用。乘数整体右移，这样乘数最左边就多出来一个数位。除此之外，将部分积整体右移，左边拿0补，右边移出的数不能丢保存到乘数寄存器的第一位。

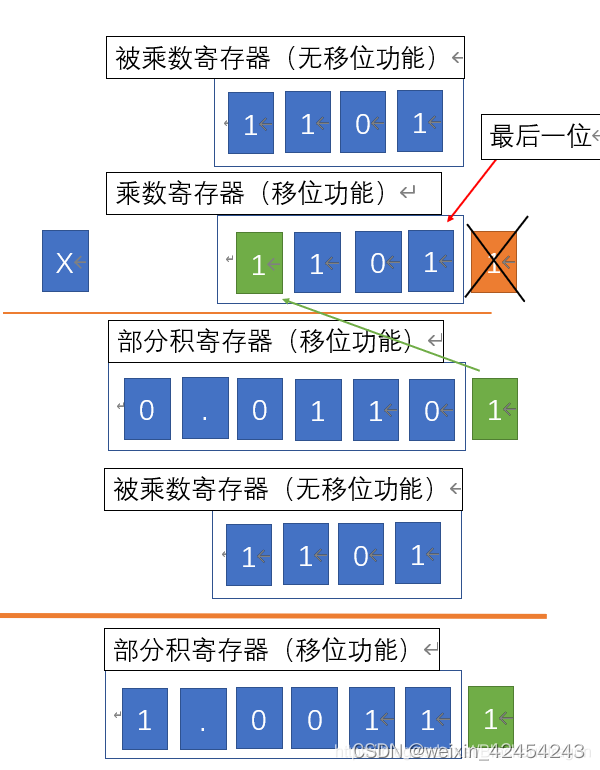
以乘数新的最后一位进行判定，然后与部分积进行相加

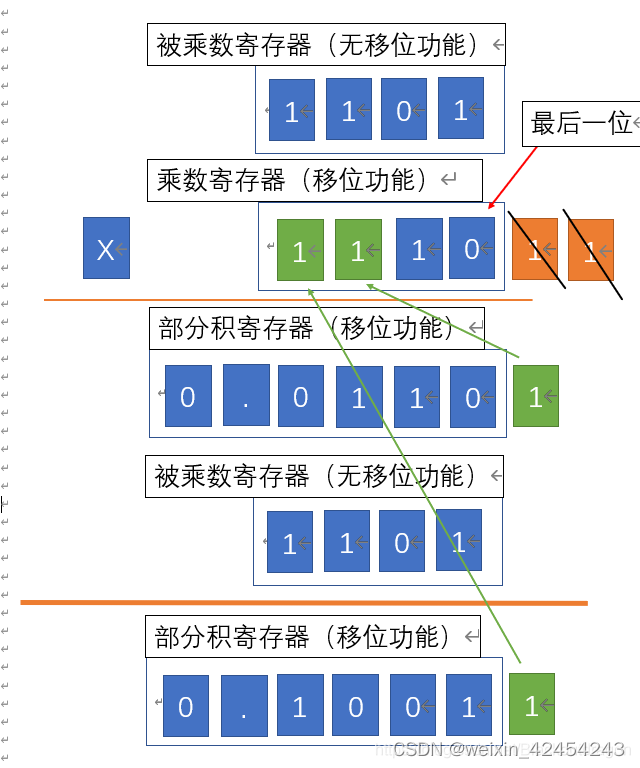
再次进行移位操作，将乘数的最后一位右移删除，空出的最高位由部分积的移出的最低位补充


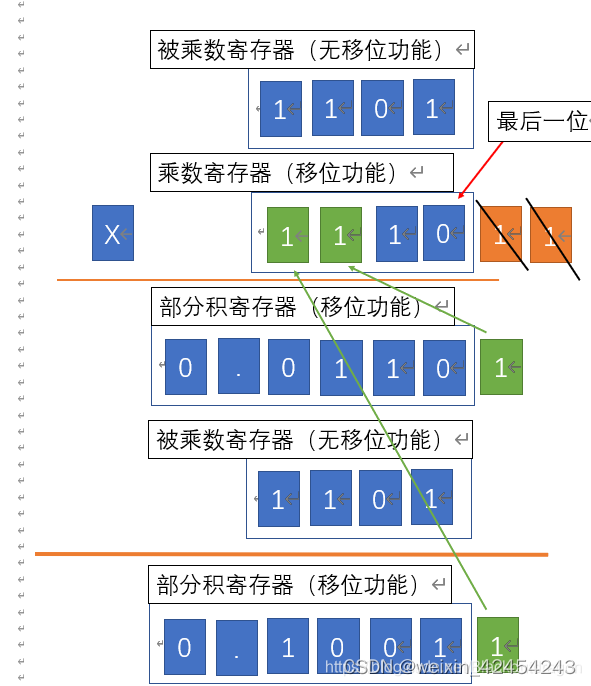
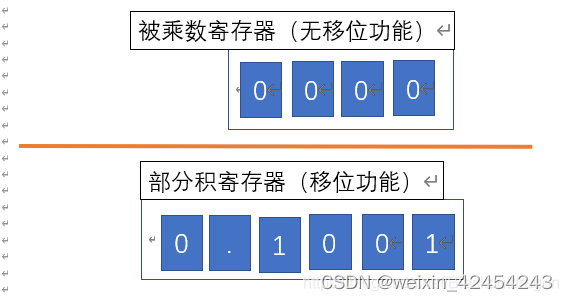
乘数的最后一位是0，不用再加上被乘数，所以结果直接为部分寄存器中的值


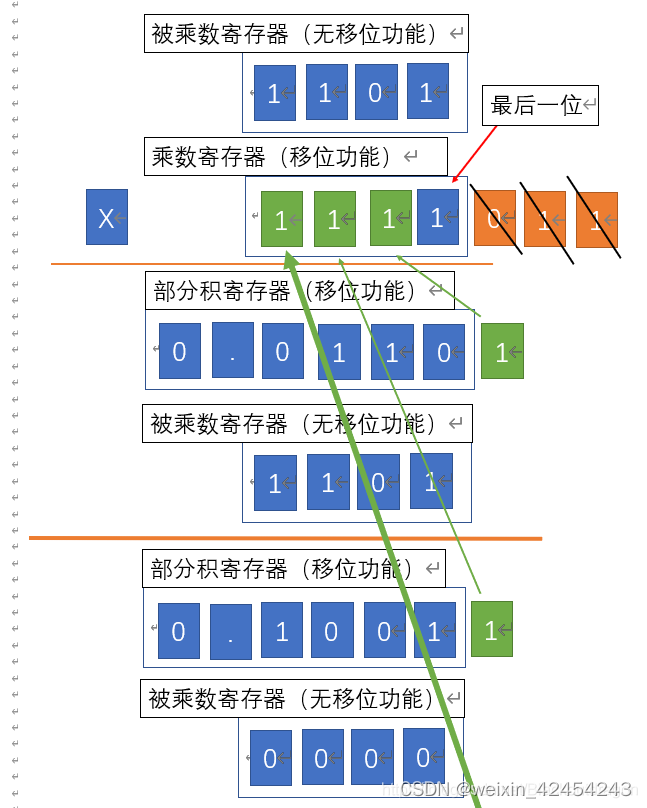
注意：这里虽然加上的是0，但是在实际操作中，是没有这一步的，但是控制移位是必修要进行的

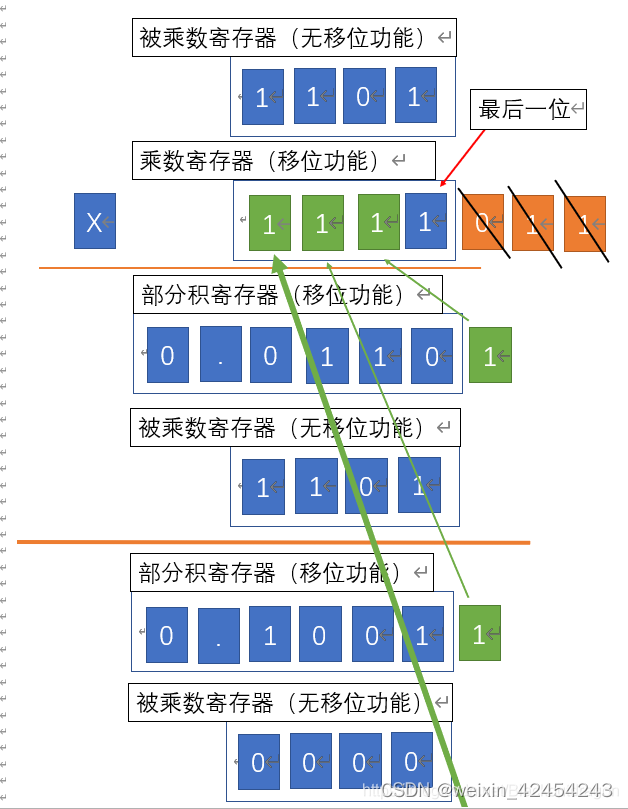
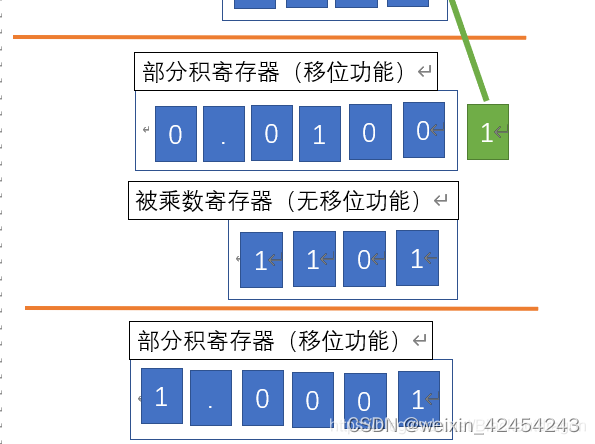
将乘数最后一位进行判定，加上被乘数


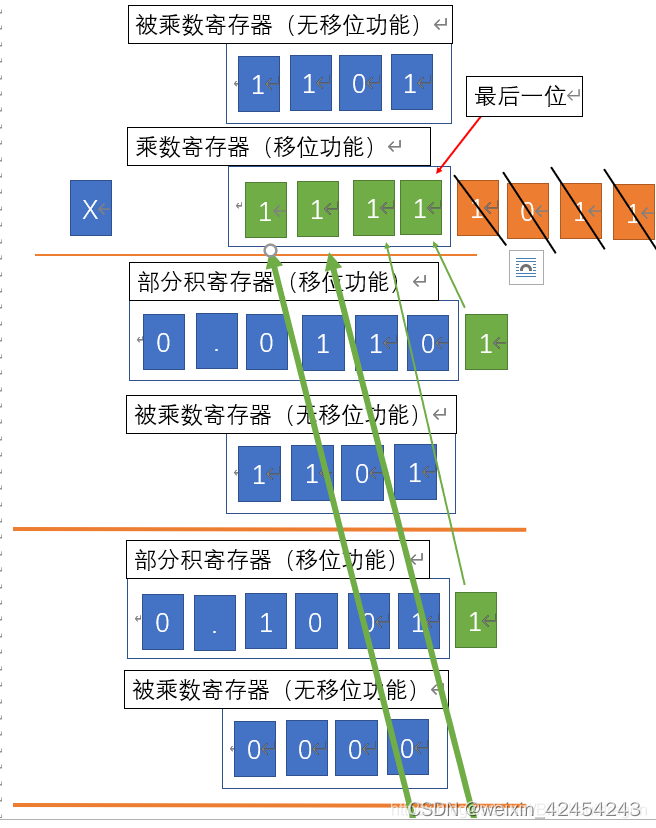
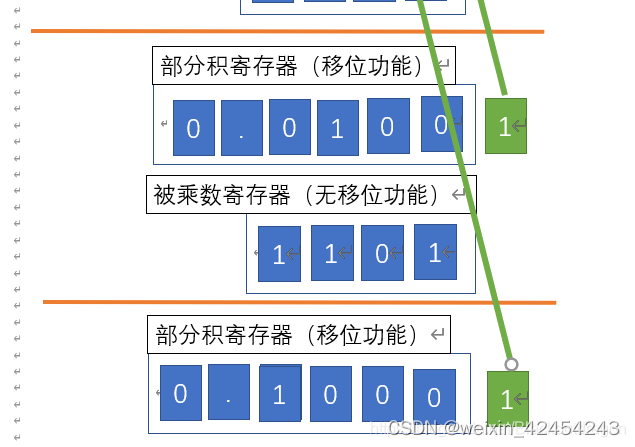
进行移位运算，最终结果是部分积寄存器中的高位和乘数寄存器中的低位组合，就是最终的结果

4.4 硬件配置

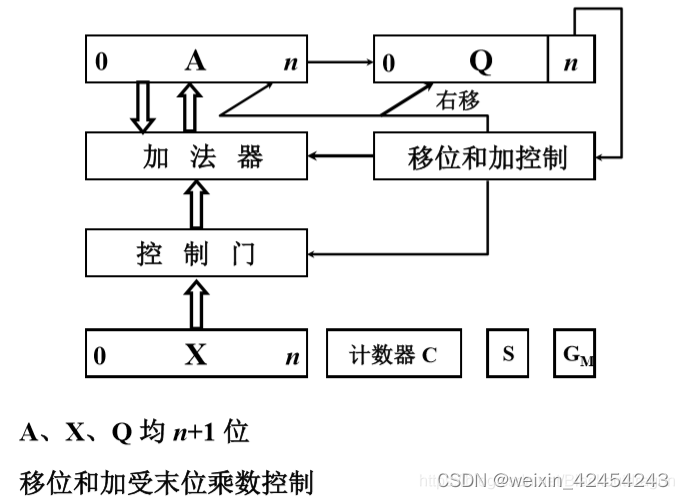
A为移位寄存器，用来保存部分积
Q为移位寄存器，用来保存乘数和部分积的低位部分
X为通用寄存器，用来保存被加数
C为计数器，用来控制整个乘法的运行步骤和循环次数

4.5 表格示意图

例题：已知x=-0.1110 y=0.1101 求[x·y]原


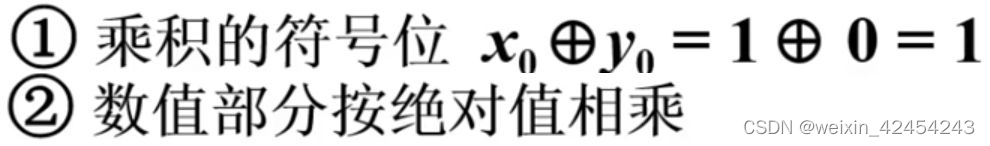
则[x·y]原=1.10110110

特点：
绝对值运算
用移位的次数判断乘法是否结束

5. 除法运算

5.1 分析笔算除法

X=-0.1011 y=0.1101 求x/y

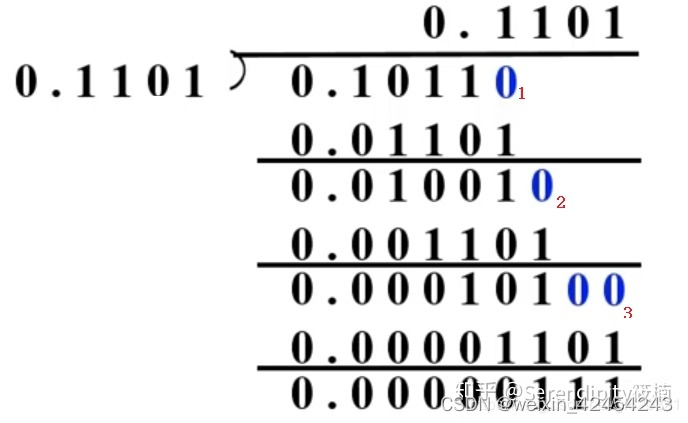
x/y=-0.1101
余数 0.00000111

1. 上商后补0，和右移1位的除数0.01101做比较，比现在加0后的被除数小，上1，减掉右移1位的除数；
2. 添0，和右移2位的除数做比较，小数后有2个0，显然比现在的余数小，上商1，减掉右移2位的除数，得到新余数；
3. 添0，把新余数和右移3位的除数0.0001101做比较，比现在的余数大，上商0，继续给新的余数添0，和右移4位的除数0.00001101做比较，比新余数小，上商1，减法得到余数

当商的位数和除数的位数一样时停止

5.2 笔算除法和机器除法比较

5.3 原码除法

以小数为例

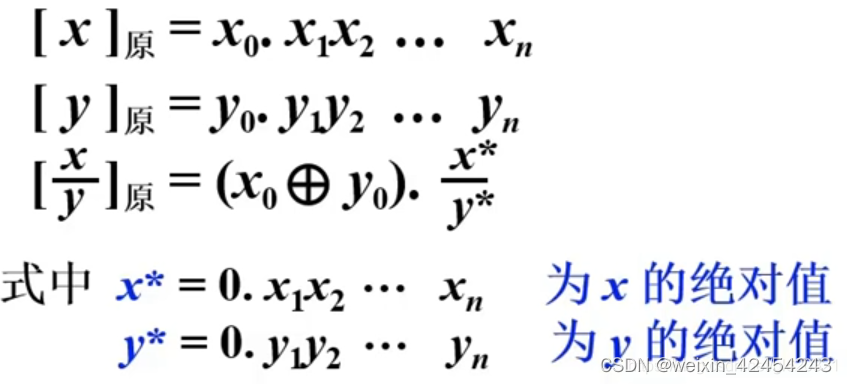
特点
商的符号位单独处理x与y异或运算
数值部分为绝对值相除x^* / y^*
小数定点除法x^* < y^* 整数定点除法x^* > y^*
被除数不等于0，除数不能为0

5.3.1 恢复余数法

恢复余数法运算规则

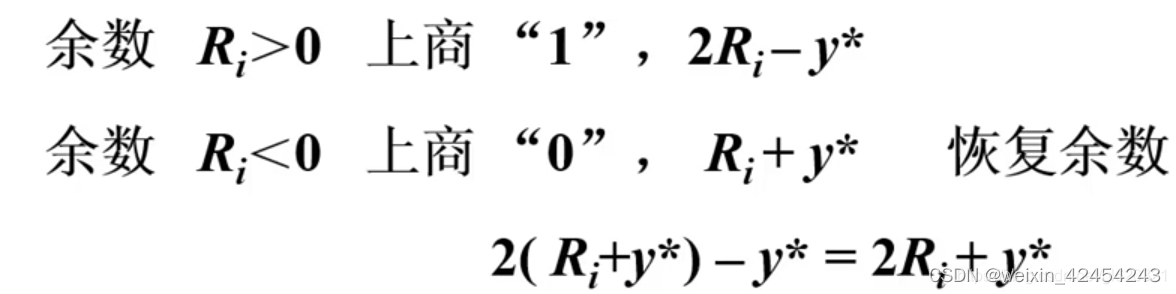
例题：
x=-0.1011 y=-0.1101 求[x/y]原
解：[x]原=1.1011
[y]原=1.1101
[y^* ] 补=0.1101
[-y ^* ]补=1.0011

做减法目的：试探上商为1还是0

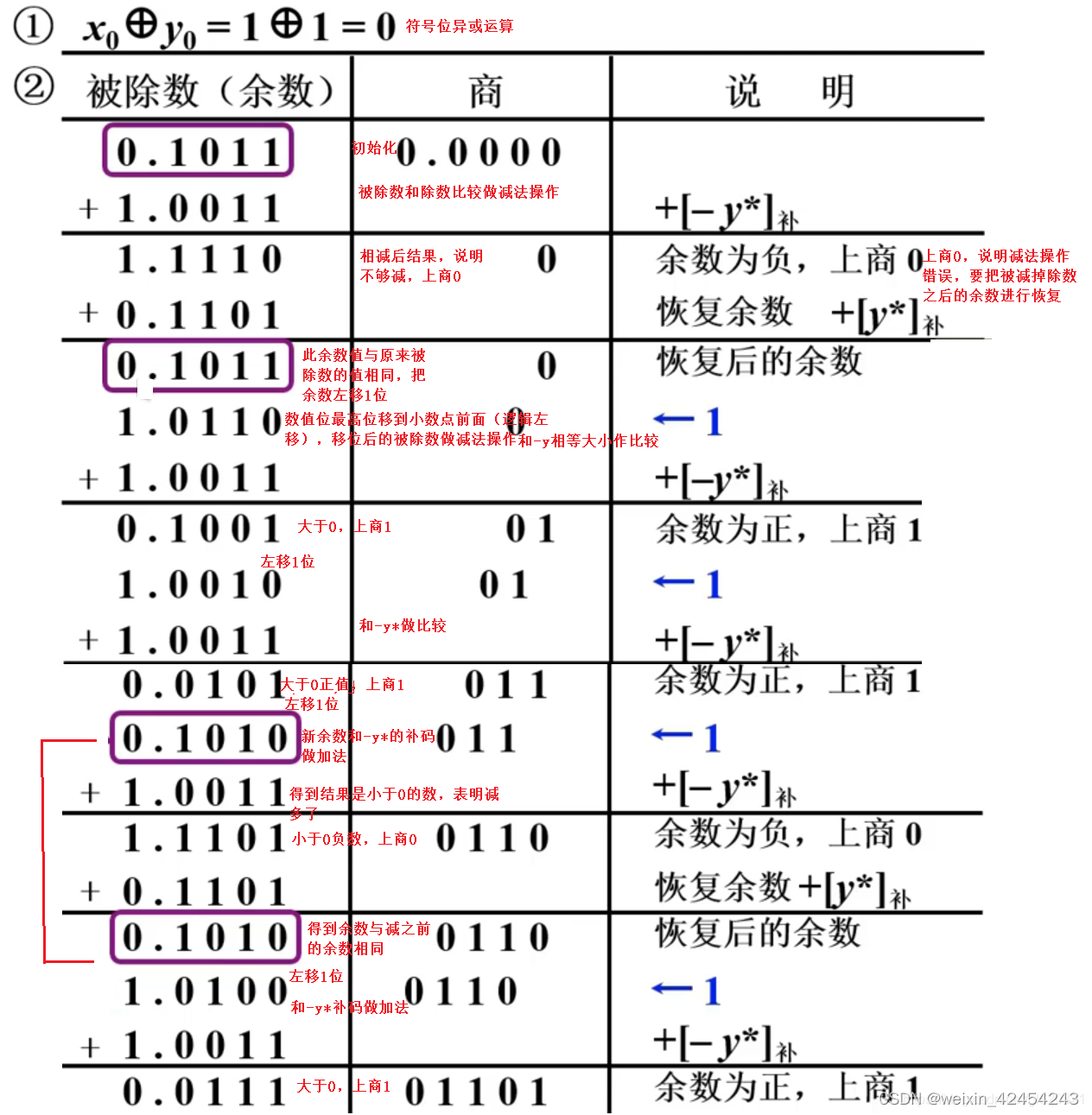
所有x^* / y^*=0.1101
[x/ y]原=0.1101

一共进行了5次上商，4次移位，第一次上商判断是否发生溢出：
若在小数定点机中，第一次上商上1，说明发生溢出，商的值大于1，所有只能表示绝对值小于1的数

特点：
余数为正：上商1
余数为负，上商0，恢复余数

5.3.2 不恢复余数法（加减交替法）

不恢复余数法运算规则（加减交替）

例题：
x=-0.1011 y=-0.1101 ，求[x/y]原
解：[x]原=1.1011 [y]原=1.1101 [y*]补=0.1101 [-y*]补=1.0011

符号位x=1与y=1异或得到为0
x^* / y^*=0.1101
[x/y]原=0.1101

特点：
上商n+1次
第一次上商判断是否溢出（判断被除数和除数直接的大小关系）
在小数定点机中，被除数的绝对值大于除数的绝对值，第一次上商为1就发生了溢出，移位n次，直到第一次上商处于最后一位的商的值移到符号位的位置；做了n+1次加法
用移位的次数判断除法是否结束