第二章 数制与编码
2.1 进制之间的转换
掌握:二进制、八进制、十六进制(末位加H表示)、十进制及彼此之间的转换;
问:小数怎么转换?
十进制转二进制:乘以权值再累加,如小数点后第一位的权值是2^(-1)
二进制转二进制:乘积取余法:
注意:任意二进制小数都可以用十进制表示,但不是所有十进制小数都可以用二进制表示,如0.3
问:计算机内部为什么用二进制表示
1.二进制的运算规则简答
2.制造两个稳态的物理器件比阶容易
3.便于用逻辑门电路实现运算
2.2真值、机器数、无符号整数
真值:一个普通的数据,带符号,比如-0.98,2,3,
机器数:把符号数字化的数,常用的是0正1负
无符号整数:默认全整,因为没有符号位所有全部位都可以用来表示数字,例如:如果字长8,最大可以表示11111111,最小是00000000,即0~255
无符号整数的加减:
加:从末位开始逐位相加,逢二进一
减法:被减数不变,减数各个位取反末尾再加一,减法变加法,这里与后面补码的加减异曲同工。
注:计算机常用无符号整数表示主存地址。
2.3定点数的表示
定点整数可以用原码、反码、补码、移码表示,其中,计算机一般
定点小数只可以用原码、反码、补码表示,因为移码只能用来表示整数(移码一般用于浮点数的阶码)
2.3.1原码
最高位表示符号,通常为0正1负,其他都是数值位。
0的表示形式:有两种,以八位为例,正0 :00000000,负0 :10000000
表示范围:n+1位,整数原码的表示范围为 -(2n-1)~(2n-1) 闭区间
小数的表示范围为-(1-2-n)~(1-2-n)闭区间 一定注意不是所有十进制小数都可以用二进制表示
优点:与真值的对应关系简单直观、与真值的转换简单,而且原码实现乘法运算简单
缺点:原码加减运算困难,符号位不能参与运算,原码的0有两种表示形式
2.3.2 反码
非考试重点,理解的过程产物。原码的符号位不变,数值位取反获得。0的表示形式也有两种,表示范围也与原码一致。
2.3.3 补码
考试重点。由反码末位+1得到,0的表示形式唯一,即00000000
表示范围比原码多1,即10000000表示-128,负数部分比原码可以表示的多一。
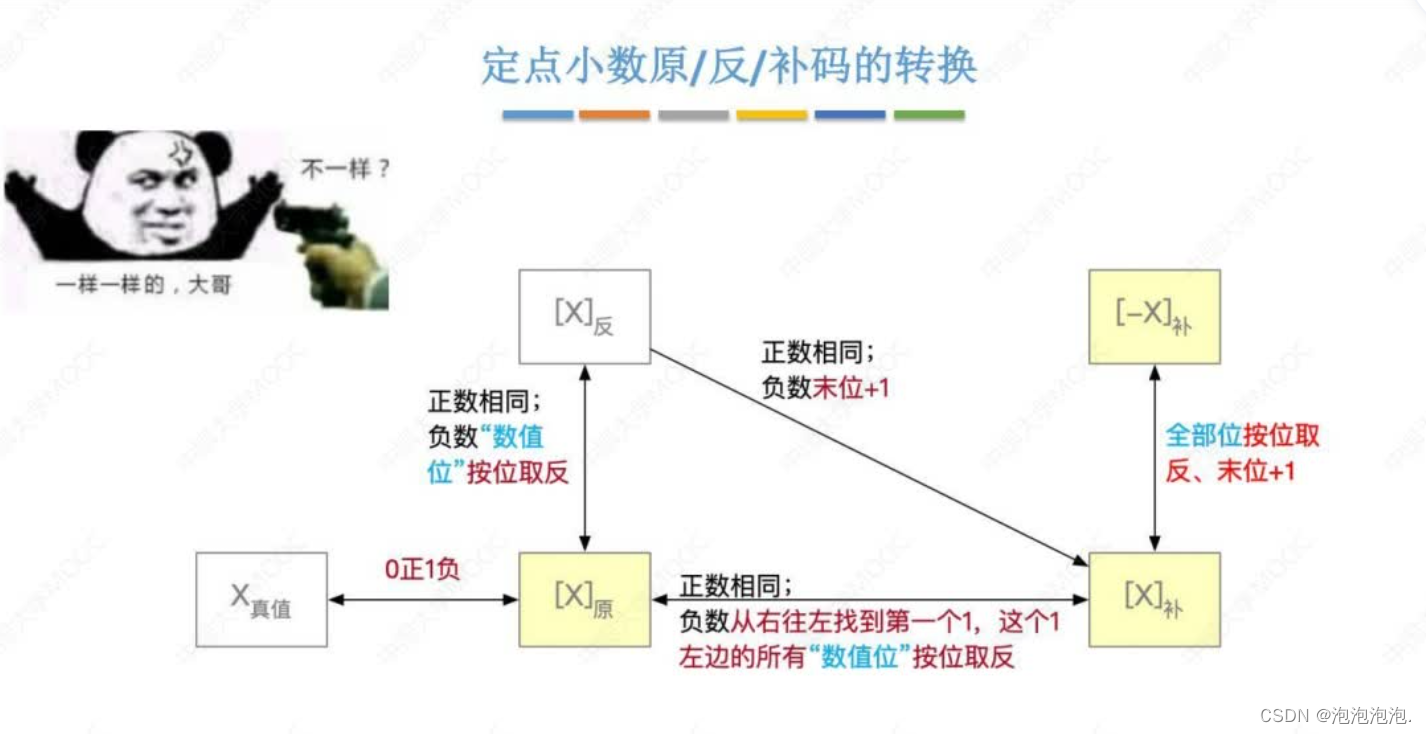
原码和原码之间的两种转换方式:分正负,详见最后图示。
计算机一般用补码进行运算,因为补码的符号位可以参与运算。
补码的运算:
加法:直接逐位相加
减法:被减数不变,减数变成相反数,即【A】补-【B】补=【A】补+【-B】补
如何从【B】补求【-B】补:所有位取反,末位+1
变形补码/模四补码:双符号位00表示正,11表示负Z
补码的特点:
1.零的表示唯一
2.符号位可以和数值位一起参与运算
3.减法可以用加法来实现
2.3.4 移码
补码的符号位不变,其他位取反得到。只能用来表示整数,一般被应用于浮点数阶码的表示。
移码的本质是加了2^n
2.3.5 总结:转换形式、表示范围
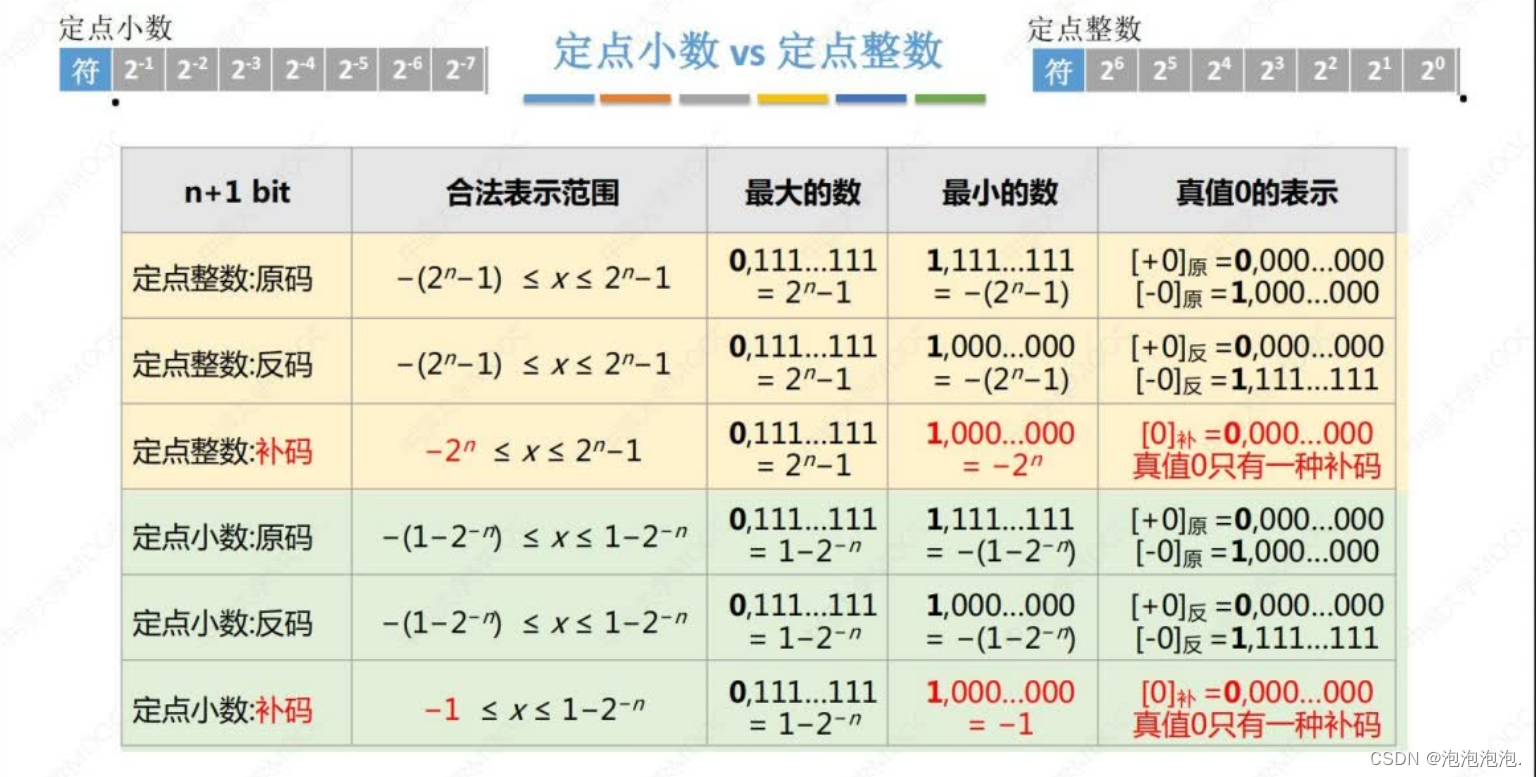






![[计算机组成原理]2-4、定点数详解](https://img-blog.csdnimg.cn/f89911ec3b3f439dae8c7ec9d27c5c95.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80ODMxMjQ4NA==,size_16,color_FFFFFF,t_70#pic_center)