一，进制

（1）全国各地最熟悉也最习惯的进制–十进制数

1.十进制

对于十进制的话就我们平常计数经常用的如1， 52 ，100这样类似的计数数字都是十进制数，计数规则是逢十进一（就是小学加法的那种+），它是由0~9共10给数码组成的，十进制数可用后缀D标识。

2.基数

我们经常把计数符号的个位数称为**基数，常用符号R**来表示。

3.十进制数的权位展开式

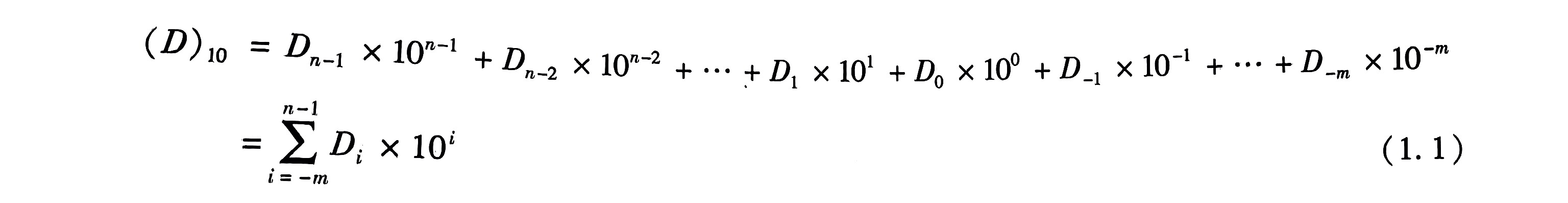
4.十进制权位展开式的理解

式中Di取值范围为0≤Di≤R-1。n为整数部分的位数，m 为小数部分的位数。整数第i位的权是R^i-1，小数点后第m位的权是R^-m。此式表示的就是各符号与其所在位权值乘积的代数和。

5.十进制对于计算机的局限

但是对于计算机而言的话，他仅仅只知道“0”和“1”也就是它处理数据用的二进制。

（2）计算机所能理解的进制–二进制数

1.二进制

对于二进制他是计算机系统常用的数，如1011，1001这样类似的计数都是二进制，计数规则是逢二进一，它是又0，1这两个数码组成的。

2.数据存储

在计算机中，根据存储介质的物理特性，数据采用二进制进行存储的。数据最小的单位是比特（又名bit，b），1bit就是表示一个二进制位。二进制数常用后缀B表示

3.常见信息量单位换算关系

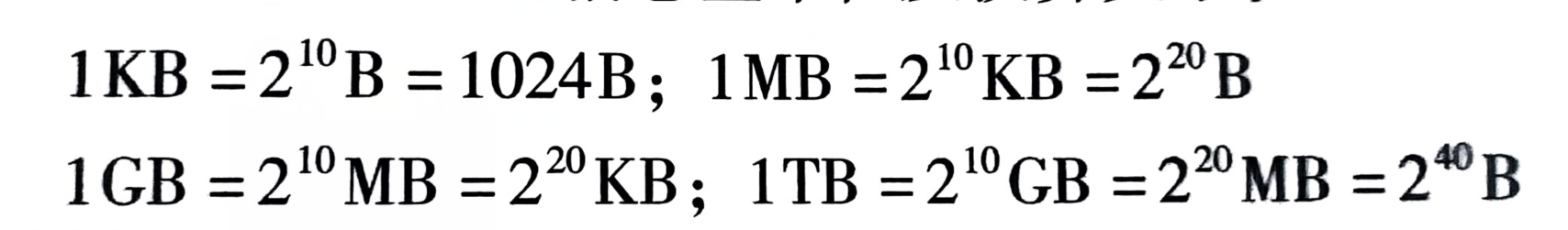
4.二进制的权位展开式

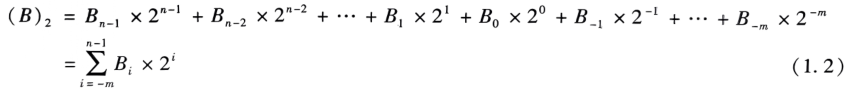
5.局限性：

通常表示一个较大的数，比较难以记忆而且复杂，因此诞生了八进制和十六进制。

（3）人类为了偷懒而发明的进制–八进制数和十六进制数

1.八进制数

八进制数它是由0~7八个数码组成，计数规则是逢八进一，常用后缀O标识

2.八进制数的表示

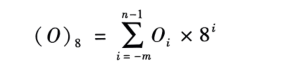
3.十六进制数

十六进制数它是由0_{F十六个数码组成**</u>，计数规则是逢十六进一<u>**其中A}F的等值十进制发别为10-15，常用后缀H标识。

4.十六进制数的表示

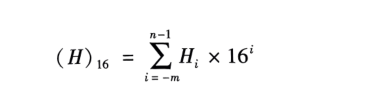
二，进制的转换

注：先提到八，十六和二进制互转是为后面不熟悉到熟悉服务

（1）八，十六进制和二进制互转

1.二进制转换为八进制

（参考(7条消息) 进制转化（二进制，八进制，十进制，十六进制）详细教程_李奇同学喵喵呜～的博客-CSDN博客）

2.八进制转换为二进制

3.二进制转换为十六进制

4.十六进制转换为二进制

5.八进制转十六进制

总体思路是：1.八进制转二进制。2.二进制再转十六进制。

6.对于转换的个人理解

对于为什么方法要划分为3个一组和4个一组，如八进制的话有8个数码也就是2³的数码对应的幂次数3不正是所要划分的组数吗

（2）熟悉到不熟悉以及不熟悉到熟悉

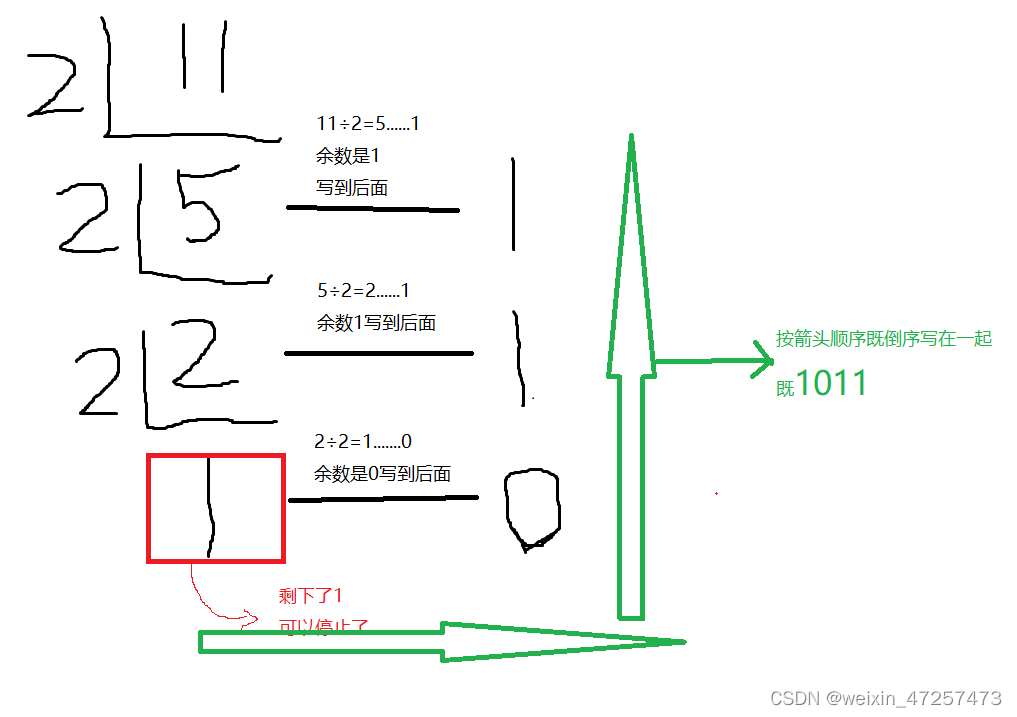
1.十进制转换为二进制

整数部分

方法一

对此根据参考的博客，我们应该从权重去了解能够更简单的知道如何转换，比如随便给几个十进制数如下

十进制数	权重运算	二进制数
15	15=1x20+1x21+1x22+1x23	1111
11	11=1x20+1x21+0x22+1x23	1011
65	65=1x20+0x21+0x22+0x23+0x24+0x25+1x26	100001

权重

正如上表所示像二进制整数部分从右到左的第一位到第n位的权重分别是2⁰,2¹……，2^n-1。

方法二

相对于方法一而言，方法二就略显复杂换算方法如下图所示

小数部分

对于小数部分的话比如10.25

方法

0.25我们先乘以2得到0.5，取整数部分0作为小数的第一位。再继续乘以2,0.5乘以2得到1.0，整数部分为1作为小数的第二位，此时由于小数部分已经为0，停止相乘。所以小数部分是01。整数部分如上面方法介绍可得为1010，我们结合起来，所以是1010.01。

2.十进制转换为八，十六进制

方法

将十进制转换为二进制，再将二进制转换为十六，八进制即可

3.八，十六，二进制转换为十进制。

方法

将八，十六进制转换为二进制，再将二进制转换为十进制即可

4.总结

其实对于进制的转换最主要的还是二进制和十进制，无论是任何的复杂转换，二进制和十进制都是必要的媒介

三，定点数和浮点数

（1）定点数

1.什么是定点数

我们都知道，数字既包括整数，又包括小数，而小数的精度范围要比整数大得多，所以如果我们想在计算机中，既能表示整数，也能表示小数，关键就在于这个小数点如何表示？于是人们想出一种方法，即约定计算机中小数点的位置，且这个位置固定不变，小数点前、后的数字，分别用二进制表示，然后组合起来就可以把这个数字在计算机中存储起来，这种表示方式叫做「定点」表示法，用这种方法表示的数字叫做「定点数」。

2.定点的划分

由于定点数的**小数点位置国定所以可以分为定点小数和定点整数**

定点小数：用于表示纯小数，小数点隐含固定在最高数据位的左边，整数位则用符号位。

定点整数：用于表示纯整数，小数点位置隐含固定在最低位之后，最高位为符号位。

3.什么是浮点数

以上关于定点数，其中「定点」指的是约定小数点位置固定不变。那浮点数的「浮点」就是指，其小数点的位置是可以是漂浮不定的。这怎么理解呢？

其实，浮点数是采用科学计数法的方式来表示的，例如十进制小数 8.345，用科学计数法表示，可以有多种方式：

8.345 = 8.345 * 10⁰
8.345 = 83.45 * 10^-1
8.345 = 834.5 * 10^-2

看到了吗？用这种科学计数法的方式表示小数时，小数点的位置就变得「漂浮不定」了，这就是相对于定点数，浮点数名字的由来。

4.浮点数的表示

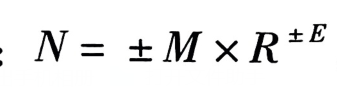
5，浮点数表示的理解

其中，尾数M为定点小数。尾数的位数决定了浮点数有效数值的精度，尾数的符号代表了浮点数的正负，因此又称为**数符**。在机器中，为了方便浮点数大小的比较，通常将数符放置在浮点数的首位。
阶码 E为定点整数，阶码的数值大小决定了该浮点数实际小数点位置与尾数的小数点位置（隐含)之间的偏移量，阶码的位数多少决定了浮点数的表示范围。阶码的符号叫阶符。

阶码的底R一般为2、8或16，且隐含规定。根据IEEE 754国际标准，常用的浮点数

6.常用的浮点数格式

类型	总位数	尾数位数	阶码位数	真值计算
短实数	32	24	8	N=(-1)MX(1,M1,M2……Mn)X2E-127
长实数	64	53	11	N=(-1)MX(1,M1,M2……Mn)X2E-1023
临时实数	80	65	15	/

注：尾数位数含一位数符，阶位数含一位阶符

7.浮点数的规格化

为了充分利用尾数的二进制数位来表示更多的有效数字，将尾数的绝对值限定在某个范
围之内，这种操作就叫浮点数的规格化。
例如R=2，则规格化浮点数的尾数M应满足条件:最高有效位为1,即-1/2≤|M|≤1。为便于计算机硬件对尾数的机器数形式的规格化判断，通常采用下列方法实现判定：（1）对于原码表示的尾数，当最高有效位为1时，浮点数为规格化，即尾数为×.1×…×形式；
（2）对于补码表示的尾数，当符号位与最高有效位相异时，浮点数为规格化，即尾数为0.1×…×形式或者为1.0×…×形式。
对于非规格化浮点数，可以通过修改阶码和左右移尾数的方法来使其变为规格化浮点数，这个过程叫作规格化。
尾数进行右移实现的规格化，则称为右规；尾数进行左移实现的规格化，则称为左规。

8.规格化浮点数的优点

提高了浮点数据的精度；使程序能够更方便地交换浮点数据；可以使浮点数的运算更为简化。